Dodécadodécaèdre adouci inversé
- Dodécadodécaèdre adouci inversé
-
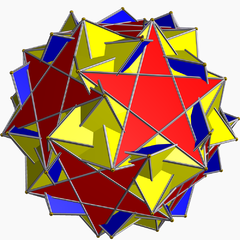
En géométrie, le dodécadodécaèdre adouci inversé est un polyèdre uniforme non-convexe, indexé sous le nom U60.
Coordonnées cartésiennes
Les coordonnées cartésiennes pour les sommets d'un dodécadodécaèdre adouci inversé centré à l'origine sont toutes les permutations paires de
- (±2α, ±2, ±2β),
- (±(α+β/τ+τ), ±(-ατ+β+1/τ), ±(α/τ+βτ-1)),
- (±(-α/τ+βτ+1), ±(-α+β/τ-τ), ±(ατ+β-1/τ)),
- (±(-α/τ+βτ-1), ±(α-β/τ-τ), ±(ατ+β+1/τ)) et
- (±(α+β/τ-τ), ±(ατ-β+1/τ), ±(α/τ+βτ+1)),
avec un nombre pair de signes plus, où
- β = (α2/τ+τ)/(ατ−1/τ),
où τ = (1+√5)/2 est le nombre d'or (quelquefois écrit φ) et α est la solution réelle négative de τα4−α³+2α²−α−1/τ, ou approximativement −0,3352090. En prenant les permutations impaires des coordonnées ci-dessus avec un nombre impair de signes plus, cela donne une autre forme, l'énantiomorphe de ce polyèdre.
Voir aussi
Lien externe
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Dodécadodécaèdre adouci inversé de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Dodecadodecaedre adouci inverse — Dodécadodécaèdre adouci inversé Dodécadodécaèdre inversé adouci Type Polyèdre uniforme Éléments F=84, A=150, S=60 (χ= 6) Faces par cotés 60{3}+12{5}+12{5/ … Wikipédia en Français
Dodécadodécaèdre Adouci Inversé — Dodécadodécaèdre inversé adouci Type Polyèdre uniforme Éléments F=84, A=150, S=60 (χ= 6) Faces par cotés 60{3}+12{5}+12{5/ … Wikipédia en Français
Polyèdre adouci — En géométrie, un polyèdre adouci est un polyèdre obtenu en écartant les faces d un polyèdre et en comblant les trous par des triangles équilatéraux. Souvent, cela consiste à remplacer chaque sommet du polyèdre par un triangle équilatéral et… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Polyèdre uniforme — Un polyèdre uniforme (en) est un polyèdre qui a pour faces des polygones réguliers et tel qu il existe une isométrie qui applique un sommet quelconque sur un autre. Il en découle que tous les sommets sont congruents, et que le polyèdre… … Wikipédia en Français
Liste Des Polyèdres Uniformes — Les polyèdres uniformes et les pavages forment un groupe bien étudié. Ils sont listés ici pour une comparaison rapide de leurs propriétés et de leurs noms de schéma variés ainsi que de leurs symboles. Cette liste inclut : tous les 75… … Wikipédia en Français
Liste des polyedres uniformes — Liste des polyèdres uniformes Les polyèdres uniformes et les pavages forment un groupe bien étudié. Ils sont listés ici pour une comparaison rapide de leurs propriétés et de leurs noms de schéma variés ainsi que de leurs symboles. Cette liste… … Wikipédia en Français
Liste des polyèdres uniformes — Cette liste recense les polyèdres uniformes, ainsi que certaines de leurs propriétés. Sommaire 1 Méthodologie 2 Table des polyèdres 2.1 Formes convexes (3 faces/sommet) … Wikipédia en Français