- Theoreme de Burnside (probleme de 1902)
-
Théorème de Burnside (problème de 1902)
En mathématiques, et plus précisément dans le contexte de la théorie des groupes finis, le théorème de Burnside traite des représentations d'un groupe répondant aux critères du problème de Burnside.
Ce théorème stipule que toute représentation dans un espace vectoriel de dimension finie, d'un groupe d'exposant fini possède une image de cardinal fini.
Ce théorème est nommé en l'honneur William Burnside (1852-1927), qui l'a démontré en 1905.
Ce théorème est un élément de solution d'une vaste question, nommée problème de Burnside, sur les groupes de type fini et d'exposant fini. Cette conjecture est encore ouverte en 2006.
Sommaire
Enoncé
-
- Toute représentation d'un groupe d'exposant fini dans un espace vectoriel complexe de dimension finie possède une image de cardinal fini.
Il peut s'exprimer de différentes manières, par exemple que tout sous-groupe du groupe linéaire d'un espace vectoriel de dimension finie et d'exposant fini est d'ordre fini.
Contexte
En 1902 William Burnside s'intéresse aux conjectures sur les groupes finis. Il pose en particulier la question suivante : un groupe de type fini et d'exposant fini est-il fini ? Il pressent immédiatement que la question est difficile. Cette question prend le nom de problème de Burnside 1902, la date permet de différencier cette question de sa non moins célèbre deuxième conjecture de 1906 sur l'ordre pair de tout groupe simple non abélien.
Dans l'article[1] décrivant cette conjecture, il traite le cas où l'exposant est égal à deux et à trois. le cas où n est égal à deux est relativement simple car le groupe est alors abélien. Il traite aussi, avec une relative imprécision le cas où n est égal à quatre et s'il existe deux générateurs.
En 1905 il démontre[2] le théorème de l'article. Un contre-exemple ne sera pas facile à construire. Il n'existe en effet aucune représentation de dimension fini d'un tel groupe. En 1911, ce théorème est généralisé[3] par Issai Schur (1875-1941). Un groupe de type fini n'admet que des représentations d'image de cardinal finie en dimension finie.
Il faut attendre les travaux[4] d'Efim Zelmanov (né en 1955) pour trouver le premier contre-exemple. Il reçoit en 1994 la médaille Fields pour ce résultat. Le problème reste très généralement ouvert. En 2006 par exemple, personne ne sait s'il existe un groupe d'ordre infini d'exposant cinq avec deux générateurs.
Démonstration
Les notations suivantes sont utilisées pour la démonstration : C désigne le corps des nombres complexes, V un espace vectoriel sur C de dimension finie noté n, u un endomorphisme de V et Tr désigne l'application trace du groupe linéaire GL(V) dans C. Ici, si p est un entier positif, up désigne la composée itérée p fois de u. Le sous-groupe image de la représentation est noté G, et l'algèbre de GL(V) engendrée par G est notée A.
Lemme
La démonstration s'appuie sur un lemme technique :
-
- L'endomorphisme u est nilpotent si et seulement si pour tout entier p compris entre 1 et n, up possède une trace nulle.
En effet, si u est nilpotent, alors son unique valeur propre est zéro, et il en est de même pour ses puissances. Sa trace, ainsi que celle de ses puissances est nulles.
Réciproquement, supposons que la trace de u ainsi que de ses puissances soient nulles. Soient P[X] son polynôme caractéristique, k le nombre de ses valeurs propres, (λi) la famille de ses valeurs propres, si i est un entier entre 1 et k, et αi l'ordre de multiplicité de λi, c'est à dire :
![P[X]=\prod_{i=1}^k (X-\lambda_i)^{\alpha_i}](/pictures/frwiki/53/58966e29e83838e3583e1b45f553b4af.png)
Si i est un entier compris entre 1 et n, la trace de ui vérifie l'égalité suivante :
![(i)\quad \forall i \in [1,n] \quad Tr(u^i)=\sum_{j=1}^k \alpha_j . \lambda_j^i=0](/pictures/frwiki/50/2c943843a9d61a9f388870aa19443871.png)
Pour s'en rendre compte, il suffit par exemple d'opérer une réduction de Jordan sur une matrice de u. La famille (αi) est annulée par la matrice (λij) si i et j sont des entiers entre 1 et k. On trouve alors une matrice de Vandermonde. On en déduit que zéro est valeur propre. En retranchant la valeur propre zéro du système d'équation (i), on obtient une nouvelle matrice de Vandermonde, l'unique valeur propre possible est donc zéro.
Le polynôme minimal est alors une puissance de X, ce qui signifie que u est nilpotent.
Théorème
Si le groupe G est fini, alors le théorème de Lagrange prouve qu'il est d'exposant fini.
Réciproquement, A est une algèbre de dimension finie, il existe donc une famille (gi) pour i variant de 1 à m qui est une base de cette algèbre. Soit φ l'application linéaire de A dans Cm définie par :
![\forall a \in A \quad \varphi(a)= \Big (Tr(a\circ c_i)\Big )_{i \in [1,m]}](/pictures/frwiki/52/4b8623d890bd9c03ee4777a614f33208.png)
Le théorème se démontre en trois temps :
-
- Si a et b sont deux éléments de A ayant même image par φ alors si k est un entier positif, la trace de ( ab-1 )k est égale à n.
Tout d'abord, on remarque que si m est un élément quelconque que A, alors les traces de am et de bm sont égales. En effet, la famille des ci est génératrice de l'espace vectoriel A et la trace est linéaire. Calculons alors la trace de ( ab-1 )k.

La deuxième égalité est vraie car les deux derniers facteurs sont des éléments de A. Une récurrence permet de conclure que la trace de ( ab-1 )k est égale à celle de l'identité et donc à n.
-
- L'application φ est injective.
Pour cela, déterminons la trace des puissances de ab-1 - Id où Id désigne l'endomorphisme identité. Si k est un entier positif, la formule du binôme de Newton montre que :
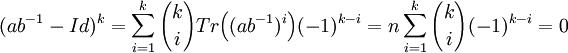
L'endomorphisme ab-1 - Id est nilpotent d'après le lemme. Or ab-1 est un endomorphisme diagonalisable car, si e désigne l'exposant du groupe G, il admet comme polynôme annulateur Xe - 1, c'est à dire un polynôme scindé sans racine multiple. En effet, l'endomorphisme est diagonalisable si et seulement si le polynôme minimal est scindé sans racine multiple (cette propriété est démontrée dans l'article polynôme d'endomorphisme).
Soit une base de vecteurs propres de ab-1, c'est aussi une base de vecteurs propres de l'identité et donc de ab-1 - Id. Ce dernier endomorphisme est donc à la fois diagonalisable et nilpotent, ce qui démontre qu'il est égale à l'endomorphisme nul. On en déduit que ab-1 est égal à l'identité ou encore que a est égal à b et la proposition est démontrée.
-
- Le groupe G est d'ordre fini.
Si g est un élément de G alors les seules valeurs propres sont les racines e-ièmes de l'unité. On en déduit que la trace de g ne peut prendre qu'un nombre fini de valeurs et que l'ensemble d'arrivé de φ est fini. Comme φ est injective, G est un ensemble fini. Ce qui termine la démonstration.
Notes et références
Notes
- ↑ William Burnside On an unsettled question in the theory of discontinuous groups Quart.J.Math. 33 pages 230 à 238 1902
- ↑ William Burnside On criteria for the finiteness of the order of a group of linear substitutions Proc.London Math. Soc. (2) 3 pages 435 à 440 1905
- ↑ Issai Schur Über Gruppen periodischer substitutionen Sitzungsber. Preuss. Akad. Wiss. pages 619 à 627 1911
- ↑ Efim Zelmanov Solution of the restricted Burnside problem for groups of odd exponent Math. USSR Izvestiya 36 (1) pages 41 à 60 1991
Liens externes
- (en) A history of the Burnside's problem Par le site de l'université de St Andew
- (fr)[pdf] Théorème de Burnside par M. Pellerin
Références
- (en) Marshall Hall, The theory of groups [détail des éditions]
- Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808)[détail des éditions]
- X. Gourdon Algèbre Ellipse 1994
- Portail des mathématiques
Catégories : Théorie des représentations | Théorème d'algèbre -
Wikimedia Foundation. 2010.

