Representation induite d'un groupe fini

Representation induite d'un groupe fini

Représentation induite d'un groupe fini

En mathématiques une représentation induite est une méthode de construction d'une représentation d'un groupe. Cet article traite le cas des groupes finis.

Une représentation induite permet de construire à l'aide d'un sous-groupe une représentation du groupe.

Sommaire

Définitions et exemples

Définitions

Dans tout l'article, G désigne un groupe fini d'ordre g, (V, ρ) une représentation de G dans un espace vectoriel sur un corps K de caractéristique différente de deux et tel que les caractères irréductibles de G forment une base orthonormale des fonctions centrales à valeur dans K. On peut prendre par exemple pour K le corps des nombres complexes. H désigne un sous-groupe de G et (W, θ) une sous-représentation de la restriction de ρ à H.G/H désigne l'ensemble des classes à gauche modulo H.

Une première remarque est nécessaire avant d'établir la définition d'une représentation induite :

  • Soit s et t deux éléments de G choisis dans une même classe à gauche modulo H, les espaces vectoriels image de W par ρs et ρt sont égaux.

En effet, il existe un élément u de H tel que t = su, et donc si o désigne la composition de fonctions, alors ρt est égal à ρsoρu. Or l'image de W par ρu est égal à W, car ρu est un automorphisme laissant W stable.

Soit c une classe à gauche de G/H, Wc désigne l'image par ρs, où s est un élément de c, de W. Il devient alors possible d'exprimer la définition d'une représentation induite :

  • La représentation (V, ρ) est dite induite par celle de (W, θ) si et seulement si V est la somme directe des espaces Wc quand c parcourt G/H. Dans ce cas, la représensation ρ est noté Ind (θ) ou encore IndHG (θ) si un risque d'ambiguïté existe.
  • Le caractère de ρ est appelée caractère induit de G par la représentation θ. Si χ désigne le caractère de θ, celui de ρ est noté Ind (χ) ou encore IndHG (χ) si un risque d'ambiguïté existe.

Ces définitions possèdent un sens car il existe une et une unique représentation de G induite par θ. La démonstration est donnée à la suite dans cet article.

L'induction possède une réciproque, elle correspond à la restriction de la représentation au sous-groupe H. Cette restriction est noté Res (ρ) ou encore ResHG (ρ) si un risque d'ambiguïté existe.

Exemples

Les deux articles Représentations du groupe symétrique d'indice trois et Représentations du groupe des quaternions utilisent les représentations induites pour construire une représentation irréductible.

  • Si H est le sous-groupe trivial de G, alors, la représentation induite sur G par la représentation triviale de H - qui est la seule représentation irréductible de H - est la représentation régulière.
  • Soit (W, θ) la représentation régulière de H, La représentation régulière de G possède comme base canonique une base partionnée par les classes à gauche de H. En conséquence, la représentation régulière de G est induite par (W, θ).
  • Si H=G, alors l'induction de H à G est une opération triviale.

Propriétés

Premières propriétés

Les représentations induites héritent ce certaines propriétés immédiates :

  • Soit (W, θ) une représentation du sous-groupe H, (V, ρ) la représentation induite sur G et E un sous-espace stable de ρ. Alors la restriction de ρ à E est induite par la restriction de θ à E.

En effet, soient c une classe à gauche, Wc l'image de W à gauche par ρs si s est un élément de c et Ec l'intersection de Wc et E. Les intersections deux à deux des Ec, si c décrit l'ensemble des classes à gauche est réduite au vecteur nulle car celles des Wc le sont. Leur somme génère bien l'espace E car celle des Wc est égale à V, ce qui démontre la proposition.

  • Soient (W1, θ1) et (W2, θ2) deux représentations de H, (V1, ρ1) et (V2, ρ2) deux représentations de G induites par les précédentes, alors la représentation somme directe de V1 et V2 est induite par la représentation somme directe de W1 et W2.

La démonstration est analogue à la précédente.

Il existe une propriété fondamentale sur les représentations induites :

  • Il existe une et une seule représentation induite de G par (W, θ) à un isomorphisme près.

Si W est identifié à un H-module et si (V, ρ) est la représentation induite, alors, en identifiant V à un K[G]-module, on obtient l'égalité tensorielle :

V=K[G]\otimes_{K[H]}W \;

De plus la structure d'origine et celle induite disposent d'une analogie forte :

  • Si (V, ρ) est la représentation induite par (W, θ) et si (E, σ) est une représentation de G, les deux algèbres HomH (W, Res E) et HomG (V, E) sont isomorphes.

Cette propriété est l'équivalence, entre terme de morphismes de la loi de réciprocité de Frobenius.


Démonstrations

L'utilisation des G-modules et du produit tensoriel montre de manière naturelle l'existence et l'unicité de la représentation induite :

  • K[G] est une représentation de G induite par K[H].

Il suffit pour cela de remarquer que K[G] est un K[H] de base C si C est un système de représentants des classes à gauche de H dans G. Soit s un élément de C, K[H].s est l'image de K[H].1 par l'application linéaire qui à h élément de K[H] associe h.s, c’est-à-dire l'image de K[H].1 par le point s de la représentation. Le fait que les K[H].s soit une somme directe égale à K[G] est la conséquence du fait que C est une base.

Si (W, θ) est une représentation de H, alors W est un K[H]-module. Considérons alors le produit tensoriel de W et de K[G], tout deux considérés comme des K[H]-modules :

I=K[G]\otimes_{K[H]}W \quad W'=1_{K[G]}\otimes_{K[H]}W

Ce produit tensoriel I correspond au module déduit de W par extension des scalaires K[H] à K[G].

  • Le module I est la représentation induite de G par (W, θ).

En effet, W' est isomorphe à W en tant que K espace vectoriel et la représentation θ est isomorphe à la représentation multiplication externe par un élément de H. Soit c un élément de C, c.W' forme bien une somme directe égale à I, ce qui démontre que la représentation est bien induite.

Soit V un espace vectoriel contenant W et ρ une représentation tel que la restriction de ρ à W soit égal à θ. Considérons alors l'injection canonique de W dans V, elle se prolonge par linéarité en une application linéaire φ de I dans V. L'application φ est alors un morphisme de K[G]-module.

  • (V, ρ) est une représentation induite par (W, θ) si et seulement si φ est une bijection.

Cette proposition découle directement du fait que C est une base de K[G] en tant que K[H]-module.

On en déduit la conséquence suivante :

  • Il existe une et une seule représentation induite de G par (W, θ) à un isomorphisme près.

On dispose de la propriété :

  • Si (V, ρ) est la représentation induite par (W, θ) et si (E, σ) est une représentation de G, les deux algèbres HomH (W, Res E) et HomG (V, E) sont isomorphes.

En effet, considérons l'application de HomH (W, Res E) dans HomG (V, E), qui au morphisme f associe 1K[G]\otimesf. Cette application est bien un morphisme d'algèbre, son noyau est manifestement réduit au vecteur nul.

Montrons qu'il est surjectif, soit g un morphisme de HomG (V, E), g et (1K[G]\otimeswi) une base de I en tant que K[G]-module. Si φ désigne toujours l'isomorphisme entre I et V, alors g est défini par l'image de la base (φ(1K[G]\otimeswi)) et l'application de W dans E, qui à wi associe g (φ(1K[G]\otimeswi)) est bien l'antécédent dans HomH (W, Res E) de g, ce qui termine la démonstration.

Critère d'irréductibilité de Mackey

Article détaillé : Critère d'irréductibilité de Mackey.

Une double application de la formule de réciprocité de Frobenius décrite ci dessous permet de démontrer le résultat suivant, connu sous le nom de critère d'irréductibilité de Mackey. Quelques définitions sont nécessaire pour l'exprimer. Ht désigne ici le sous-groupe intersection du sous-groupe conjugué de H par t avec S, 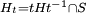\scriptstyle H_t = tHt^{-1}\cap S et si t est un élément de G, θt désigne la représentation de Ht dans W définie par :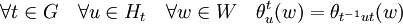

\forall t \in G \quad \forall u \in H_t \quad \forall w \in W \quad \theta^t_u(w)=\theta_{t^{-1}ut}(w)

Le critère s'applique avec une double classe sur H.

Il s'énonce de la manière suivante :

  • La représentation (V, ρ) est irréductible si et seulement si θs et la restriction de θ à Hs sont disjointes quand s est un élément de G - H.

Il existe un corollaire, dans le cas où le groupe H est distingué :

  • La représentation induite de G par celle de H (W, θ) est irréductible si et seulement si (W, θ) est irréductible et n'est isomorphe à aucune représentation conjuguée θs.

Les définitions utilisées et les démonstrations sont présentes dans l'article associé.

Caractère

Formule du caractère

Soit (W, θ) une représentation de H sur le corps K, Ind (θ) ou IndHG (θ) désigne la représentation induite de G par (W, θ), et ψ désigne le caractère de θ. Soit (V, ρ) une représentation de G sur le corps K, La restriction de cette représentation à H est notée Res (ρ) ou ResHG (ρ) et son caractère χ :

  • Si s est un élément de G, ψ désigne le caractère de θ, la représentation de H, C un système de représentants des classes de conjugaison (c’est-à-dire un représentant dans chaque classe) et h l'ordre de H, alors la valeur du caractère χ au point t de G est donnée par la formule :
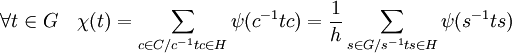
\forall t \in G \quad \chi(t)=\sum_{c\in C / c^{-1}tc \in H} \psi(c^{-1}tc) = \frac 1h \sum_{s\in G / s^{-1}ts \in H} \psi(s^{-1}ts)\;

Il est possible de généraliser la fonction IndHG à l'espace vectoriel des fonctions centrales de H de la manière suivante :

  • Soit f une fonction centrale de H à valeur dans K et C un système de représentants des classes à gauche, alors la fonction IndHG (f ) est définie de la manière suivante :
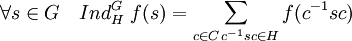
\forall s \in G \quad Ind_H^G \; f(s) = \sum_{c\in C \, c^{-1}sc \in H} f(c^{-1}sc) \;

La démonstration est donnée dans l'article Réciprocité de Frobenius.

Réciprocité de Frobenius

Article détaillé : Réciprocité de Frobenius.

Avec les notations du paragraphe précédent, la formule de réciprocité de Frobenius s'exprime par :

  • Les deux scalaires suivants sont égaux :
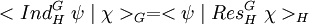
<Ind_H^G \;\psi\; |\; \chi>_G=<\psi\; |\; Res_H^G\; \chi>_H

Il est possible de généraliser la formule :

  • Soit f une fonction centrale de H et g une fonction centrale de G, alors l'égalité suivante est vérifiée :
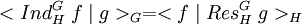
<Ind_H^G \; f\; |\;g>_G=<f\; |\;Res_H^G \; g>_H

Une autre manière d'exprimer cette propriété est la suivante :

  • L'application IndHG est l'adjointe de ResHG.

Notes et références

Articles sur les Représentations d'un groupe d'ordre fini
Représentations d'un groupe fini | Théorie des représentations | Théorème de Maschke | Caractère | Lemme de Schur | Représentation régulière | Fonction centrale | Produit tensoriel | Algèbre d'un groupe fini | Représentation induite | Réciprocité de Frobenius | Critère d'irréductibilité de Mackey | Groupe symétrique d'indice trois | Groupe symétrique d'indice quatre | Groupe des quaternions | Théorème de Burnside (groupe résoluble) | Théorème de Burnside (problème de 1902)

Notes

Liens externes

Références

  • Jean-Pierre Serre, Représentations linéaires des groupes finis [détail des éditions]
  • (en) Marshall Hall, The theory of groups [détail des éditions]
  • Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808) [détail des éditions]
  • N. Bourbaki Algèbre, Chapitre VIII Paris, Hermann 1958
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Repr%C3%A9sentation induite d%27un groupe fini ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Representation induite d'un groupe fini de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Représentation induite d'un groupe fini — En mathématiques une représentation induite est une représentation d un groupe canoniquement associée à une représentation de l un de ses sous groupes. L induction est adjointe à gauche de la restriction (en). Cette propriété intervient dans …   Wikipédia en Français

  • Theorie des representations d'un groupe fini — Théorie des représentations d un groupe fini Ferdinand Georg Frobenius, fondateur de la théorie de la représentation des groupes. En mathématiques et plus précisément en théorie des groupes, la théorie des représentations d un groupe fini est un… …   Wikipédia en Français

  • Caractere d'une representation d'un groupe fini — Caractère d une représentation d un groupe fini Fichier:Ferdinand Georg Frobenius.jpg Ferdinand Georg Frobenius fondateur de la théorie des caractères En mathématiques le caractère d une représentation d un groupes finis est un outil utilisé pour …   Wikipédia en Français

  • Caractère D'une Représentation D'un Groupe Fini — Fichier:Ferdinand Georg Frobenius.jpg Ferdinand Georg Frobenius fondateur de la théorie des caractères En mathématiques le caractère d une représentation d un groupes finis est un outil utilisé pour analyser les représentations d un groupe fini.… …   Wikipédia en Français

  • Caractères d'une représentation d'un groupe fini — Caractère d une représentation d un groupe fini Fichier:Ferdinand Georg Frobenius.jpg Ferdinand Georg Frobenius fondateur de la théorie des caractères En mathématiques le caractère d une représentation d un groupes finis est un outil utilisé pour …   Wikipédia en Français

  • Théorie des caractères d'un groupe fini — Caractère d une représentation d un groupe fini Fichier:Ferdinand Georg Frobenius.jpg Ferdinand Georg Frobenius fondateur de la théorie des caractères En mathématiques le caractère d une représentation d un groupes finis est un outil utilisé pour …   Wikipédia en Français

  • Théorie des caractères d'une représentation d'un groupe fini — Caractère d une représentation d un groupe fini Fichier:Ferdinand Georg Frobenius.jpg Ferdinand Georg Frobenius fondateur de la théorie des caractères En mathématiques le caractère d une représentation d un groupes finis est un outil utilisé pour …   Wikipédia en Français

  • Caractère d'une représentation d'un groupe fini — En mathématiques le caractère d une représentation d un groupe fini est un outil utilisé pour analyser les représentations d un groupe fini. Le caractère d une représentation (V, ρ) d un groupe G correspond à l application de G dans le corps de l …   Wikipédia en Français

  • Théorie des représentations d'un groupe fini — Ferdinand Georg Frobenius, fondateur de la théorie de la représentation des groupes. En mathématiques et plus précisément en théorie des groupes, la théorie des représentations d un groupe fini traite des représentations d un groupe G dans le cas …   Wikipédia en Français

  • Representation irreductible — Représentation irréductible En mathématiques, une représentation irréductible est un concept utilisé dans le cadre de la théorie des représentation d un groupe. Une représentation irréductible est une représentation qui n admet qu elle même et la …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”