Caractere d'un groupe fini

Caractere d'un groupe fini

Caractère d'un groupe fini

En mathématiques, un caractère d'un groupe fini est une notion associée à la théorie des groupes.

Un caractère d'un groupe fini G est un morphisme du groupe G dans C* le corps des nombres complexes non nuls.

Ce concept permet de définir le groupe dual de G, composé de l'ensemble des caractères de G. Il est à la base de l'analyse harmonique sur les groupes finis.

Cette notion correspond à un cas particulier de caractère d'une représentation d'un groupe fini.

Sommaire

Définitions et exemples

Définitions et premières propriétés

Dans tout l'article, G désigne un groupe fini d'ordre g, C le corps des nombres complexes et C* l'ensemble des nombres complexes non nuls. Sauf mention contraire, le groupe est noté multiplicativement et l'inverse d'un élément s de G est noté s-1. Le conjugué d'un nombre complexe z est noté z*.

  • Un caractère de G est un morphisme du groupe G dans C*.

Un caractère correspond à un cas particulier de représentation d'un groupe fini, celui où l'espace vectoriel de la représentation est celui des nombres complexes. Dans ce contexte, un caractère est aussi le caractère d'une représentation au sens de la trace.

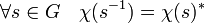
\forall s \in G \quad \chi(s^{-1}) = \chi(s)^* \;

En effet, le théorème de Lagrange indique que si s est un élément de G, alors sg = 1, on en déduit que l'image de s par χ est une racine g-ième de l'unité et toute racine g-ième de l'unité admet pour inverse son conjugué.

  • L'ensemble des caractères de G est appelé groupe dual de G et est généralement noté \scriptstyle \widehat G .

Le dual de G est naturellement munis d'une multiplication, celle des fonctions à valeur dans C :

En effet, le dual de G est non vide car il contient au moins l'application qui à tout élément de G associe l'unité, ce caractère est l'élément neutre du groupe. L'associativité est une propriété générale de la multiplication des fonctions. Si χ est un caractère, l'application qui à tout élément de G associe le conjugué de χ est un caractère qui correspond à l'inverse de χ, tout élément du dual possède donc un symétrique. Enfin le corps des nombres complexes est commutatif, ce qui implque le caractère abélien du dual de G.

Un caractère est une application d'un ensemble de départ fini et son image, contenue dans le groupe des racines g-ièmes de l'unité est aussi fini, ce qui démontre que le dual est un groupe fini.

Premiers exemples

Considérons le cas ou G est le groupe symétrique d'indice n. L'application signature est un caractère à valeur dans {-1, 1}.

Si G est égal à Z/2.Z où Z désigne l'ensemble des entiers naturels, alors il existe deux caractères, celui qui à la classe de 1 associe 1 et celui qui associe -1.

Si G est égal à Z/3.Z, alors il existe trois caractères, défini par les trois valeurs que peuvent prendre l'image de la classe de 1 : 1, j ou j*. Ici j désigne la racine cubique de l'unité ayant une partie imaginaire positive.

Cas commutatif

Dans le cas où G est commutatif, le groupe dual possède une propriété intéressante, il est isomorphe à G, ce qui permet simplement de construire une analyse harmonique sur G.

Groupe cyclique

Article détaillé : Groupe cyclique.

Dans ce pararagraphe le groupe cyclique d'ordre g est noté Cg et ω désigne une racine primitive g-ième de l'unité, c'est-à-dire un générateur du groupe des racines g-ièmes de l'unité. Le symbole 1C désigne ici un générateur du groupe Cg et si s est un entier compris entre 0 et g - 1, alors sC désigne la valeur s.1C.

Un cas simple d'analyse du groupe dual correspond au groupe cyclique, il est décrit par les propositions suivantes :

  • Pour tout caractère χ de Cg, il existe un entier i compris entre 1 et g - 1 tel que l'égalité suivante est vérifiée :
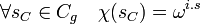
\forall s_C \in C_g \quad \chi(s_C) = \omega^{i.s}\;
  • Réciproquement, si i est un entier compris entre 1 et g - 1 et si χi est l'application définie par l'égalité suivante, alors χi est un caractère de Cg.
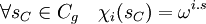
\forall s_C \in C_g \quad \chi_i(s_C) = \omega^{i.s}\;
  • Si i est un entier compris entre 1 et g - 1, alors l'application de Cg dans son dual, qui à iC associe χi est un isomorphisme de groupe.


Démonstrations
  • Pour tout caractère χ de Cg, il existe un entier i compris entre 1 et g - 1 tel que l'égalité suivante est vérifiée :
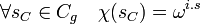
\forall s_C \in C_g \quad \chi(s_C) = \omega^{i.s}\;

χ(1C) est une racine de l'unité et ω est une racine primitive, il existe donc un entier i compris entre 1 et g - 1 tel que χ(1C) est égal à ωi. Les propriétés de morphisme de χ montre l'égalité suivante, ce qui permet de conclure :

\forall s \in [0, g-1] \quad \chi(s_C)=\chi(s.1_C)=\chi(1_C)^s=\omega^{i.s}\;
  • Si i est un entier compris entre 1 et g - 1 et si χi est l'application définie par l'égalité suivante, alors χi est un caractère de Cg.
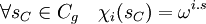
\forall s_C \in C_g \quad \chi_i(s_C) = \omega^{i.s}\;

Il suffit de vérifier que χi est bien un morphisme de groupe. Cette propriété découle des égalités suivantes :

\forall s_C, t_C \in C_g \quad \chi_i(s_C.t_C) = \chi_i(st. 1_C) = \omega^{i.st}=\chi_i(s_C).\chi_i(t_C)\;
  • Si i est un entier compris entre 1 et g - 1, alors l'application φ de Cg dans son dual, qui à iC associe χi est un isomorphisme de groupe.

Vérifions que l'application φ est un morphisme :

\forall i,j \in [0, g-1] \quad \forall s_C\in C_g \quad \varphi(i_C+j_C)(s_C)=\chi_{i_C+j_C}(s_C)= \omega^{(i+j)s} = \omega^{is}.\omega^{js} = \chi_i(s_C).\chi_j(s_C)=\varphi(i_C)(s_C).\varphi(j_C)(s_C)\;

Le noyau de φ est réduit à l'élément neutre, l'application est donc injective, de plus les deux propositions précédentes montre que l'ordre du groupe dual est égal à g, le cardinal de Cg, l'application est donc surjective, ce qui termine la démonstration.

Groupe abélien

Article détaillé : Théorème de Kronecker.

Les résultats du paragraphe précédent se généralisent à tous les groupes abéliens finis:

  • Le dual d'un groupe abélien fini G est isomorphe à G.

Ce résultat découle du fait qu'un groupe abélien fini est un produit de groupes cycliques et de la proposition suivante :

  • Soit H et K deux groupes abéliens, le dual du produit direct de H et de K est isomorphe au produit des duals de H et de K.


Démonstrations
  • Soit H et K deux groupes abéliens, le dual du produit direct de H et de K est isomorphe au produit des duals de H et de K.

Notons iH (resp. iK) le morphisme canonique de H (resp. K) dans HxK. Considérons alors le morphisme ψ du dual de HxK dans le produit des duals défini par :

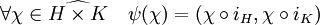
\forall \chi \in \widehat {H\times K} \quad \psi (\chi) = (\chi \circ i_H , \chi \circ i_K) \;

L'application ψ est un morphisme injectif, soit χH, χK deux éléments des duals de H et de K. On remarque que l'application χHxK de HxK dans C* définie par :

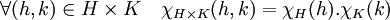
\forall (h,k) \in H\times K \quad \chi_{H \times K}(h,k)=\chi_H(h).\chi_K(k) \;

est un caractère de HxK antécédent de (χH, χK). L'application ψ est donc bien surjective. Ce qui termine la démonstration.

  • Le dual d'un groupe abélien fini G est isomorphe à G.

Le théorème de structure des groupes abéliens finis (cf l'article associé) montre que G est isomorphe à un produit de groupe cycliques. Une récurrence sur le nombre de cycles et la proposition précédente permet alors de conclure.

Algèbre du groupe

Article détaillé : Algèbre d'un groupe fini.

Ici G désigne un groupe fini quelconque, C[G] désigne l'algèbre complexe du groupe G et (es) la base canonique de l'algèbre indexée par les éléments s de G.

L'algèbre du groupe G, noté ici C[G] est un espace vectoriel de base canonique indexée par G. Un élément du groupe dual de G se prolonge linéairement en un élément du dual de C[G] considéré comme un espace vectoriel. Il est donc possible d'identifier le groupe dual de G comme un sous-ensemble de l'espace dual de C[G].

Si C[G] est muni du produit hermitien canonique < | >, défini par la formule suivante, alors le dual de C[G] s'identifie avec l'algèbre du groupe, le groupe dual est donc identifié avec un sous-ensemble de C[G] :

\forall x,y \in \mathbb C[G] \quad \exists (x_s)_{s \in G},(y_t)_{t \in G} \in \mathbb C^G \quad <x|y>=<\sum_{s \in G} x_s.e_s|\sum_{t \in G} y_t.e_t>=\frac 1g \sum_{s,t \in G} x_s^*.y_s \;
  • Le groupe dual de G est élément du centre de l'algèbre du groupe G.
  • Le groupe dual de G est une base de l'algèbre du groupe G si et seulement si G est un groupe abélien.

Ces trois propositions correspondent à des cas particuliers de la théorie des représentations d'un groupe fini, elles se démontrent simplement dans le cas présent :


Démonstrations
  • Le groupe dual de G est une famille orthonormale.

Soit χ un caractère du groupe G, alors χ*.χ = χ-1.χ = 1C[G] où 1C[G] désigne l'élément neutre de l'algèbre du groupe. On en déduit :

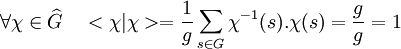
\forall \chi \in \widehat G \quad <\chi|\chi>= \frac 1g \sum_{s \in G} \chi^{-1}(s).\chi(s) = \frac gg = 1

Si χ1 et χ2 sont deux caractères distincts de G. Notons χ le caractère χ1-1.χ2 alors :

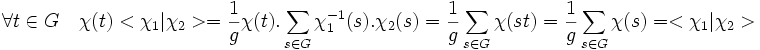
\forall t \in G \quad \chi(t)<\chi_1|\chi_2>= \frac 1g \chi(t).\sum_{s \in G} \chi_1^{-1}(s).\chi_2(s) = \frac 1g \sum_{s \in G} \chi(st)= \frac 1g \sum_{s \in G} \chi(s) = <\chi_1|\chi_2>

Si t est choisi de tel manière à ce que χ(t) soit différent de 1, alors on en déduit que χ1 et χ2 sont orthogonaux.

  • Le groupe dual de G est inclus dans le centre de l'algèbre du groupe G.

Il suffit pour cela de remarquer que tout caractère du groupe est une fonction centrale et que l'ensemble des fonctions centrales est le centre de l'algèbre.

  • Le groupe dual de G est une base de l'algèbre du groupe G si et seulement si G est un groupe abélien.

Le groupe dual est une famille orthogonale, elle est donc libre. Si le groupe G est abélien, le groupe dual possède le même cardinal que le groupe G donc son ordre est celui de la dimension de l'algèbre du groupe.

Si le groupe G n'est pas abélien son algèbre associé ne l'est pas non plus, le groupe dual engendre un espace vectoriel inclus dans le centre de C[G] qui n'est pas égal à l'algèbre entière.

Bidual

Dans le cas où le groupe G est abélien, et de manière analogue à l'algèbre linéaire, il existe un isomorphisme canonique entre G et son bidual (c'est-à-dire le dual de son dual).

  • L'application φ, définie par l'égalité suivante, est un isomorphisme entre G et son bidual :
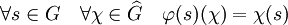
\forall s \in G \quad \forall \chi \in \widehat G \quad \varphi(s)(\chi) = \chi(s) \;

En effet, l'application φ est un morphisme injectif, l'égalité des cardinaux d'un groupe abélien et de son dual démontre la surjectivité et termine la démonstration.

Applications

Analyse harmonique sur un groupe abélien fini

Article détaillé : Analyse harmonique sur un groupe abélien fini.

Dans le cadre d'un groupe abélien fini, il est possible de définir la transformée de Fourier et le produit de convolution. La théorie de l'analyse harmonique est analogue à celle du corps des réels. On démontre l'égalité de Parseval, le théorème de Plancherel, la dualité de Pontryagin et la formule sommatoire de Poisson.

Notes et références

Liens externes

Références

  • Michel Demazure Cours d'algèbre. Primalité, divisibilité, codes Cassini 1997
  • Jean-Pierre Serre, Cours d'arithmétique [détail des éditions]
  • A. Warusfel Structures algébriques finies Hachette 1971
  • G. Peyré L'algèbre discrète de la transformée de Fourier Ellipses Marketing 2004
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Caract%C3%A8re d%27un groupe fini ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Caractere d'un groupe fini de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Caractère D'un Groupe Fini — En mathématiques, un caractère d un groupe fini est une notion associée à la théorie des groupes. Un caractère d un groupe fini G est un morphisme du groupe G dans C* le corps des nombres complexes non nuls. Ce concept permet de définir le groupe …   Wikipédia en Français

  • Caractère d'un groupe fini — En mathématiques, un caractère d un groupe fini est une notion associée à la théorie des groupes. Un caractère d un groupe fini G est un morphisme de groupes de G dans le groupe multiplicatif ℂ* des nombres complexes non nuls. Ce concept permet… …   Wikipédia en Français

  • Caractere d'une representation d'un groupe fini — Caractère d une représentation d un groupe fini Fichier:Ferdinand Georg Frobenius.jpg Ferdinand Georg Frobenius fondateur de la théorie des caractères En mathématiques le caractère d une représentation d un groupes finis est un outil utilisé pour …   Wikipédia en Français

  • Caractère D'une Représentation D'un Groupe Fini — Fichier:Ferdinand Georg Frobenius.jpg Ferdinand Georg Frobenius fondateur de la théorie des caractères En mathématiques le caractère d une représentation d un groupes finis est un outil utilisé pour analyser les représentations d un groupe fini.… …   Wikipédia en Français

  • Representations d'un groupe fini — Représentations d un groupe fini En mathématiques, un groupe est une structure algébrique dont la définition est remarquablement simple. Elle consiste en un ensemble muni d une unique opération. Cette opération possède de bonnes propriétés, elle… …   Wikipédia en Français

  • Représentations d'un groupe fini — En mathématiques, un groupe est une structure algébrique qui consiste en un ensemble muni d une unique opération. Cette opération possède de bonnes propriétés, elle est associative, il existe un élément neutre et tout élément admet un inverse. Un …   Wikipédia en Français

  • Caractère d'une représentation d'un groupe fini — En mathématiques le caractère d une représentation d un groupe fini est un outil utilisé pour analyser les représentations d un groupe fini. Le caractère d une représentation (V, ρ) d un groupe G correspond à l application de G dans le corps de l …   Wikipédia en Français

  • Algebre d'un groupe fini — Algèbre d un groupe fini En mathématiques, l algèbre d un groupe fini s inscrit dans le cadre de la théorie des représentations d un groupe fini. Une algèbre d un groupe fini est la donnée d un groupe fini, d un espace vectoriel de dimension l… …   Wikipédia en Français

  • Algèbre D'un Groupe Fini — En mathématiques, l algèbre d un groupe fini s inscrit dans le cadre de la théorie des représentations d un groupe fini. Une algèbre d un groupe fini est la donnée d un groupe fini, d un espace vectoriel de dimension l ordre du groupe et d une… …   Wikipédia en Français

  • Algèbre d'un groupe fini — Pour les articles homonymes, voir Algèbre (homonymie). En mathématiques, l algèbre d un groupe fini est un cas particulier d algèbre d un monoïde qui s inscrit dans le cadre de la théorie des représentations d un groupe fini. Une algèbre d un… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”