Representations du groupe des quaternions

Représentations du groupe des quaternions

En mathématiques les représentations du groupe des quaternions sont un exemple d'application de la théorie des représentations d'un groupe fini. Il illustre le théorème d'Artin-Wedderburn et met en évidence un corps gauche (id non commutatif) contenant celui des nombres réels.

Sur le corps des nombres complexes, il existe cinq représentations irréductibles que les caractères mettent rapidement en évidence.

Sur le corps des nombres réels, il existe aussi cinq représentations irréductibles dont l'une possède une propriété spécifique aux algèbres semi-simples. Les morphismes de la sous-algèbre simple associée forment un corps gauche contenant celui des réels. La configuration classique du lemme de Schur où les endomorphismes commutant avec une représentation irréductible se limitent aux homothéties n'est pas vérifiée ici.

Cette propriété, permettant de construire des corps gauches, à l'aide d'une algèbre associative est l'une des méthodes fondamentales de la théorie des corps. Le terme anciennement utilisé était nombre hypercomplexe.

Sommaire

1 Analyse du groupe des quaternions
- 1.1 Définition et propriétés du groupe
2 Représentation sur le corps des complexes
3 Représentations sur le corps des réels
4 Notes et références

Analyse du groupe des quaternions

Définition et propriétés du groupe

Article détaillé : groupe de quaternions.

Il existe de nombreuses manières de définir le groupe des quaternions. Celle utilisée ici est la définition abstraite, à partir de deux générateurs. Le groupe est noté Q₈, il est noté multiplicativement, l'élément neutre est noté 1 et les deux générateurs a et b. Ils vérifient les égalités suivantes :

$a^4=b^4=1 \; , \quad bab^{-1}=a^{-1} \; ,\quad a^2=b^2$

Sa table est la suivante :

.	1	a	-1	-a	b	ab	-b	-ab
1	1	a	-1	-a	b	ab	-b	-ab
a	a	-1	-a	1	ab	-b	-ab	b
-1	-1	-a	1	a	-b	-ab	b	ab
-a	-a	1	a	-1	-ab	b	ab	-b
b	b	-ab	-b	ab	-1	a	1	-a
ab	ab	b	-ab	-b	-a	-1	a	1
-b	-b	ab	b	-ab	1	-a	-1	a
-ab	-ab	-b	ab	b	a	1	-a	-1

L'élément -1 commute avec tous les autres, le groupe {1, -1} est donc un sous-groupe distingué isomorphe au groupe cyclique d'ordre deux, noté ici C₂. Le quotient de Q₈ par le groupe C₂ donne un groupe à quatre éléments. On reconnait le groupe de Klein noté ici V.

On en déduit que si x n'est pas élément du centre du groupe, il n'est conjugué qu'avec son opposé, par l'action de groupe des automorphismes intérieurs. Ceci montre l'existence de cinq classes de conjugaison. Deux classes sont constitués des éléments du centre : 1 = {1}, -1 = {-1} et trois autres classes, contenant deux éléments : A = {a, -a}, B = {b, -b} et AB = {ab, -ab}. Ces notations sont utilisées tout au long de l'article.

Représentation sur le corps des complexes

Caractères irréductibles

Article détaillé : Caractère d'une représentation d'un groupe fini.

Le quotient de Q₈ par C₂ est un groupe abélien isomorphe à V. Cette remarque détermine quatre caractères irréductibles correspondant à des représentations de degré un. En effet, si χ désigne un caractère de degré un de V et φ le morphisme surjectif canonique de Q₈ dans V alors χoφ est une représentation de degré un de Q₈ et donc un caractère irréductible. On note ici χ₁ le caractère de la représentation triviale et χ_X le caractère égal à -1 sur X désignant ici une des classes de conjugaison A, B ou AB et 1 ailleurs.

Le nombre de représentations irréductibles à un isomorphisme près est égal au nombre de classes de conjugaison. Il ne reste donc qu'une unique représentation irréductible ρ à trouver et son caractère associé, noté ici χ_ρ. L'image de l'élément 1 du groupe par χ_ρ est égal à deux et représente le degré de la représentation ρ. Pour s'en convaincre il suffit de remarquer que la somme des carrés des degrés des différentes représentations irréductibles du groupe est égal à son ordre. χ_ρ est de norme égal à 1 et est orthogonal aux autres caractères irréductibles. Ces considérations déterminent intégralement le dernier caractère. Résumons ces résultats dans une table :

.	1	χ_A	χ_B	χ_AB	χ_ρ
1	1	1	1	1	2
-1	1	1	1	1	-2
A	1	1	-1	-1	0
B	1	-1	1	-1	0
AB	1	-1	-1	1	0

Représentation irréductible de degré deux

Article détaillé : Représentation induite d'un groupe fini.

Une méthode rapide pour déterminer la dernière représentation est donnée par les représentations induites. Pour obtenir directement une représentation de degré deux, il est nécessaire de considérer un sous-groupe H d'ordre quatre. Définissons H comme le groupe isomorphe à C₄ engendré par a. Une représentation θ doit alors être choisie pour être ensuite induite sur Q₈. Cette représentation θ doit être choisie de telle manière à ce que la représentation induite ρ soit de caractère orthogonale avec les représentations de degré 1. La loi de réciprocité de Frobenius permet simplement de vérifier cette orthogonalité. Elle s'exprime de la manière suivante :

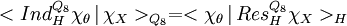
$<Ind_H^{Q_8} \chi_{\theta} \, | \, \chi_X>_{Q_8}=<\chi_{\theta} \, |\, Res_H^{Q_8}\chi_X>_H$

Sur 1 et -1 tous les cararactères des représentations de degré 1 sont égaux à 1. Sur a et -a, ils valent soit 1 soit -1. Si l'on choisit pour caractère celui qui à a associe i, alors les orthogonalités recherchées sont bien obtenues. L'utilisation du critère d'irréductibilité de Mackey et la remarque que tous les automorphismes intérieurs laissent les éléments du groupe invariant permet de conclure sans calcul. Et la représentation ρ est bien la représentation induite de θ.

Pour connaitre cette représentation, il suffit de déterminer les matrices de a et de b car ils sont générateurs du groupe. Si M_a désigne la matrice de a et M_b celle de b, on obtient :

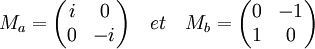
$M_a = \begin{pmatrix} i & 0 \\ 0 & -i \end{pmatrix} \quad et \quad M_b = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}$

Algèbre semi-simple

Article détaillé : algèbre semi-simple.

Dans le cas des complexes, on remarque que les quatre matrices M₁, M_a, M_b ,M_ab forment une base des matrices 2x2. En effet :

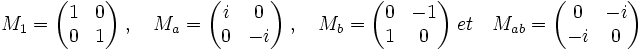
$M_1 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\; ,\quad M_a = \begin{pmatrix} i & 0 \\ 0 & -i \end{pmatrix} \; , \quad M_b = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}\; et \quad M_{ab} = \begin{pmatrix} 0 & -i \\ -i & 0 \end{pmatrix}$

Si M_c désigne la matrice de l'élément c de C[Q₈], l'algèbre C[Q₈] vérifie l'égalité :

$\forall c \in \mathbb C[Q_8] \quad \exists ! (a_i)_{i \in [1,8]} \in \mathbb C^8 \quad M_c = \begin{pmatrix} a_1 & 0 & 0 & 0 & 0 & 0 \\ 0 & a_2 & 0 & 0 & 0 & 0 \\ 0 & 0 & a_3 & 0 & 0 & 0 \\ 0 & 0 & 0 & a_4 & 0 & 0 \\ 0 & 0 & 0 & 0 & a_5 & a_7 \\ 0 & 0 & 0 & 0 & a_6 & a_8 \end{pmatrix}$

Son centre est bien égal à C⁵ et est isomorphe à l'ensemble des fonctions centrales.

Représentations sur le corps des réels

Dimension des représentations irréductibles

Article détaillé : Lemme de Schur.

Sur le corps des réels, la situation est plus délicate. Il est aisé de vérifier qu'aucun changement de base ne permet aux matrices M_a et M_b d'être à coefficients réels en même temps. La représentation irréductible complexe de dimension deux n'est donc pas réelle.

Les hypothèses qui permettent au lemme de Schur de garantir que les morphismes de sous-algèbres sont les homothéties ne sont pas rassemblées, car le corps R des réels n'est pas algébriquement clos. Il indique juste que les morphismes correspondent à des isomorphismes. La théorie des caractères est inopérante dans ce contexte.

En revanche, cette conclusion est suffisante pour appliquer le théorème de Maschke. L'algèbre comme le Q₈-module sont donc semi-simples. On en déduit que R[Q₈] est somme directe de sous-algèbres simples.

Quatre de ces sous-algèbres sont connues, elles correspondent aux représentations de degré un, qui sont toutes réelles. Il existe un supplémentaire S de la somme directe des quatre représentations de degré un stable. C'est-à-dire ayant les propriétés d'une sous-algèbre. Nous savons que S est de dimension quatre. Comme aucune sous-algèbre n'est isomorphe à une autre S ne comporte aucun facteur de dimension un. Comme toute sous-algèbre de dimension deux réelle est aussi une sous-algèbre complexe, et qu'il n'en existe qu'une, S ne comporte pas de sous-algèbre de dimension deux. Il ne peut y avoir non plus de sous-algèbre de dimension trois car il admettrait un supplémentaire stable, qui serait une sous-algèbre de dimension un. En conclusion :

L'algèbre R[Q₈] contient cinq sous-algèbres simples, quatre de dimension un et une de dimension quatre.

Représentation irréductible de degré quatre

Article détaillé : Produit tensoriel et représentations de groupes finis.

Soit V la sous-algèbre de la représentation complexe irréductible de degré deux. C'est aussi une représentation réelle de degré quatre, cette remarque est une conséquence directe d'une égalité tensorielle :

$V_{\mathbb R}=\mathbb C\otimes_{\mathbb R} V\;$

En terme matricielle, si R_x désigne la matrice réelle de M_x où x désigne un élément du groupe des quaternions, on obtient les trois égalités suivantes :

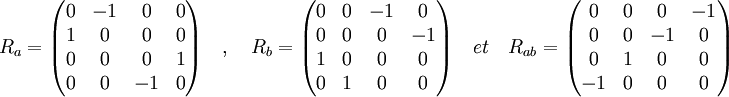
$R_a = \begin{pmatrix} 0 & -1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & -1 & 0 \end{pmatrix} \quad , \quad R_b = \begin{pmatrix} 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{pmatrix} \quad et \quad R_{ab} = \begin{pmatrix} 0 & 0 & 0 & -1 \\ 0 & 0 & -1 & 0 \\ 0 & 1 & 0 & 0 \\ -1 & 0 & 0 & 0 \end{pmatrix}$

Le caractère de a en tant que représentation complexe est nul, la représentation correspond à une somme directe de deux copies de ρ. Elle est donc bien irréductible dans R.

On vérifie que la famille (1, a, b, ab) est une base B de V_R. Notons σ la représentation associée et H_x la matrice de σ_x où x est un élément de R[V_R] dans la base B. On obtient un système de matrices très proche du précédent :

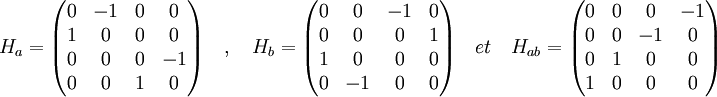
$H_a = \begin{pmatrix} 0 & -1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & -1 \\ 0 & 0 & 1 & 0 \end{pmatrix} \quad , \quad H_b = \begin{pmatrix} 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \end{pmatrix} \quad et \quad H_{ab} = \begin{pmatrix} 0 & 0 & 0 & -1 \\ 0 & 0 & -1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{pmatrix}$

On en déduit la matrice générique d'un élément de R[V_R] :

$\forall h \in \mathbb R [V_{\mathbb R}]\quad \exists ! (h_i)_{i \in [1,4]} \in \mathbb R^4 \quad / \quad H_h = h_1. 1 + h_2.a + h_3.b+h_4.ab= \begin{pmatrix} h_1 & -h_2 & -h_3 & -h_4 \\ h_2 & h_1 & -h_4 & h_3 \\ h_3 & h_4 & h_1 & -h_2 \\ h_4 & -h_3 & h_2 & h_1 \end{pmatrix}$

Morphismes de la représentation

Article détaillé : Théorème d'Artin-Wedderburn.

Recherchons l'ensemble D des morphismes du Q₈-module V_R, c'est-à-dire l'ensemble des applications d vérifant :

$\forall v_1, v_2 \in V_{\mathbb R} \quad \forall h_1, h_2 \in \mathbb R [V_{\mathbb R}] \quad d(h_1.v_1 + h_2.v_2)=h_1.d(v_1) + h_2.d(v_2) \;$

Ici, il existe un isomorphisme de module entre R[V_R] et V_R, on en déduit que R[V_R] est un anneau simple, les morphismes sont donc aisés à déterminer, si d₁ désigne la valeur d(1) on obtient :

$\forall d \in \mathbb D \quad \forall v \in \mathbb R [V_{\mathbb R}] \quad d(v) = d(v.1)=d(v).d_1 \;$

Si φ désigne l'application de D dans R[V_R] qui associe à d l'élément d₁, alors on obtient la propriété suivante :

$\forall d^1,d^2 \in \mathbb D \quad \varphi (d^1\circ d^2) = \varphi(d^2).\varphi(d^1) \quad car \quad d^1\circ d^2 (1) = d^1( d^2 (1))= d^2(1).d^1(1) \;$

Si D^op désigne l'anneau opposé de D, c'est-à-dire celui où la multiplication * est définie par l'égalité suivante, il existe un isomorphisme d'anneau entre D^op et R[V_R]:

$\forall d^1,d^2 \in \mathbb D \quad d^1*d^2=d^2\circ d^1 \quad et \quad \mathbb D^{op} = Hom^{Q_8}_{\mathbb R} (V_{\mathbb R})^{op} \simeq \mathbb R [V_{\mathbb R}] \;$

Le lemme de Schur s'applique, même si les hypothèses indiquant que les morphismes sont des homothéties ne sont pas présentes, il indique néanmoins que D^* est composée d'isomorphismes. Ce qui démontre que D est un corps gauche. Il est connu :

Le corps gauche D est nommé corps des quaternions.

Cette méthode est maintenant la principale pour construire les corps gauches et représente une branche de la théorie des corps. Initialement, un tel corps était considéré comme un ensemble de nombres hypercomplexes. On parle maintenant plutôt d'algèbre associative non commutative.

Vérification par le calcul

Déterminons la représentation matricielle de D. Pour cela notons D_δ où δ est un élément de V_R la matrice de l'élément d de D tel que φ(d) = δ. A tout élément v de V_R, d associe vδ. Si les coordonnées de δ dans la base B sont (δ_i) pour i variant de 1 à 4, on obtient :

$D_{\delta} = \begin{pmatrix} \delta_1 & -\delta_2 & -\delta_3 & -\delta_4 \\ \delta_2 & \delta_1 & \delta_4 & -\delta_3 \\ \delta_3 & -\delta_4 & \delta_1 & \delta_2 \\ \delta_4 & \delta_3 & -\delta_2 & \delta_1 \end{pmatrix}$

On vérifie alors le lemme de Schur sous une forme classique de commutativité de matrices :

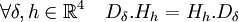
$\forall \delta, h \in {\mathbb R}^4 \quad D_{\delta}.H_h=H_h.D_{\delta}\;$

Notes et références

Articles sur les Représentations d'un groupe d'ordre fini

Notes

Liens externes

(fr) Cours de représentation des groupes finis par M. Broué de l'université de Paris VII
(fr) Représentation linéaire des groupes finis, une introduction par D. Ferrand de l'université de Rennes
(fr) Représentations linéaires des groupes finis Par Gabriel Peyré

Références

Jean-Pierre Serre, Représentations linéaires des groupes finis [détail des éditions]
(en) Marshall Hall, The theory of groups [détail des éditions]
Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808) [détail des éditions]
N. Bourbaki Algèbre, Chapitre VIII Paris, Hermann 1958

Portail des mathématiques

Ce document provient de « Repr%C3%A9sentations du groupe des quaternions ».

Catégorie : Théorie des représentations

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Representations du groupe des quaternions de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Représentations du groupe des quaternions — En mathématiques les représentations du groupe des quaternions sont un exemple d application de la théorie des représentations d un groupe fini. Il illustre le théorème d Artin Wedderburn et met en évidence un corps gauche (c est à dire non… … Wikipédia en Français
Groupe des quaternions — Graphe des cycles de Q. Chaque couleur précise une série de puissances d un élément quelconque connecté à l élément neutre (1). Par exemple, le cycle rouge reflète le fait que i 2 = 1, i 3 = i et i 4 = 1. Le cycle rouge… … Wikipédia en Français
Représentation du groupe des quaternions — Représentations du groupe des quaternions En mathématiques les représentations du groupe des quaternions sont un exemple d application de la théorie des représentations d un groupe fini. Il illustre le théorème d Artin Wedderburn et met en… … Wikipédia en Français
Groupe De Quaternions — Diagramme du cycle de Q. Chaque couleur précise une série de puissances d un élément quelconque connecté à l élément neutre (1). Par exemple, le cycle rouge reflète le fait que i 2 = 1, i 3 = i et i 4 = 1. Le cycle rouge… … Wikipédia en Français
Groupe de quaternions — Diagramme du cycle de Q. Chaque couleur précise une série de puissances d un élément quelconque connecté à l élément neutre (1). Par exemple, le cycle rouge reflète le fait que i 2 = 1, i 3 = i et i 4 = 1. Le cycle rouge… … Wikipédia en Français
Representations du groupe symetrique d'indice quatre — Représentations du groupe symétrique d indice quatre Graphe de Cayley du groupe symétrique d indice quatre en tant que groupe de rotations d un dé standard. En mathématiques les représentations du groupe symétrique d indice quatre noté S4 sont un … Wikipédia en Français
Représentations du groupe symétrique d'ordre quatre — Représentations du groupe symétrique d indice quatre Graphe de Cayley du groupe symétrique d indice quatre en tant que groupe de rotations d un dé standard. En mathématiques les représentations du groupe symétrique d indice quatre noté S4 sont un … Wikipédia en Français
Representations du groupe symetrique d'indice trois — Représentations du groupe symétrique d indice trois En mathématiques les représentations du groupe symétrique d indice trois noté S3 sont un exemple simple d application de la théorie des représentations d un groupe fini. Sur un corps de… … Wikipédia en Français
Représentations du groupe symétrique d'ordre trois — Représentations du groupe symétrique d indice trois En mathématiques les représentations du groupe symétrique d indice trois noté S3 sont un exemple simple d application de la théorie des représentations d un groupe fini. Sur un corps de… … Wikipédia en Français
Représentations du groupe symétrique d'indice quatre — En mathématiques les représentations du groupe symétrique d indice quatre noté S4 sont un exemple d application de la théorie des représentations d un groupe fini. Sur le corps des nombres complexes, il existe cinq représentations irréductibles… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Representations du groupe des quaternions

Représentations du groupe des quaternions

Sommaire