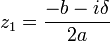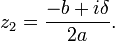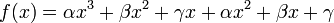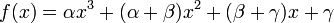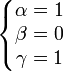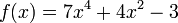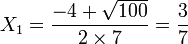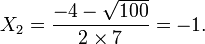- Équation algébrique
-
Équation polynomiale
Une équation polynomiale est une équation de la forme :
où les
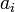 , appelés coefficients de l’équation, sont donnés. Les coefficients sont le plus souvent des nombres réels ou complexes, mais ils peuvent prendre leurs valeurs dans n’importe quel anneau.
, appelés coefficients de l’équation, sont donnés. Les coefficients sont le plus souvent des nombres réels ou complexes, mais ils peuvent prendre leurs valeurs dans n’importe quel anneau.En mathématiques, l'équation polynomiale, est le sujet central de la théorie des équations. L'objectif de la théorie des équations est de trouver les racines d'un polynôme, ce qui revient à résoudre une équation polynomiale. Résoudre l’équation consiste à trouver l’ensemble des valeurs de l’inconnue
 (appartenant à un certain ensemble, en général le même corps ou anneau que les coefficients), appelées solutions de l’équation, pour lesquelles l’équation polynomiale est vraie.
(appartenant à un certain ensemble, en général le même corps ou anneau que les coefficients), appelées solutions de l’équation, pour lesquelles l’équation polynomiale est vraie.On appelle degré de l’équation la plus grande puissance de l’inconnue affectée d’un coefficient non nul. Par exemple, l’équation
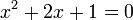 d’inconnue
d’inconnue  est une équation polynomiale réelle du second degré. (Son unique solution (solution double) est − 1.)
est une équation polynomiale réelle du second degré. (Son unique solution (solution double) est − 1.)Sommaire
Théorie
Polynômes
Soit l’équation
dont les coefficients ai appartiennent à un corps
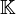 . Les solutions de (E) dans
. Les solutions de (E) dans 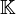 sont les racines du polynôme
sont les racines du polynômeobtenu en substituant à l'inconnue x l'indéterminée X.
On montre en algèbre qu'un polynôme de degré n possède au plus n racines. L'équation (E) admet donc au plus n solutions.
Si
 est un surcorps de
est un surcorps de 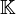 , on peut considérer (E) comme une équation à coefficients dans
, on peut considérer (E) comme une équation à coefficients dans  ; et les solutions de (E) dans
; et les solutions de (E) dans 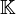 sont aussi solutions dans
sont aussi solutions dans  (la réciproque étant en général fausse). Il est toujours possible de trouver un surcorps de
(la réciproque étant en général fausse). Il est toujours possible de trouver un surcorps de 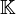 , appelé corps de rupture du polynôme P, dans lequel (E) admet au moins une solution.
, appelé corps de rupture du polynôme P, dans lequel (E) admet au moins une solution.Existence de solutions pour les équations réelles et complexes
Le théorème de d'Alembert-Gauss affirme que le corps des complexes est algébriquement clos, c’est-à-dire que toute équation polynomiale à coefficients complexes et de degré au moins un admet une solution.
Il s’ensuit que toute équation polynomiale de degré un ou plus à coefficients réels admet une solution complexe. En revanche, une équation comme x2 + 1 = 0 n’a pas de solution dans
 (ses solutions sont les complexes i et − i).
(ses solutions sont les complexes i et − i).Toutefois, une équation polynomiale réelle de degré impair admet nécessairement une solution réelle. En effet, la fonction polynôme associée est continue, et elle tend vers
 au voisinage de
au voisinage de  et vers
et vers 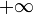 au voisinage de
au voisinage de 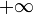 . D’après le théorème des valeurs intermédiaires, elle prend donc la valeur zéro en un certain réel, qui est ainsi solution de l’équation.
. D’après le théorème des valeurs intermédiaires, elle prend donc la valeur zéro en un certain réel, qui est ainsi solution de l’équation.Lien avec la théorie de Galois
On dispose de formules donnant les solutions des équations polynomiales réelles ou complexes de degré inférieur ou égal à 4 en fonction de leurs coefficients. Abel a montré qu’il n’est pas possible de trouver de telles formules générales (n’utilisant que les quatre opérations usuelles et les racines) pour les équations de degré 5 ou plus. La théorie de Galois donne un critère permettant de déterminer, étant donnée une équation polynomiale, si sa solution s’exprime par radicaux.
Résolution explicite des équations numériques
Démarche
La résolution explicite d’une équation réelle ou complexe du premier degré est immédiate. Résoudre une équation de degré supérieur n revient à factoriser le polynôme associé, c’est-à-dire à réécrire (E) sous la forme
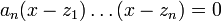 ,
,
où apparaissent naturellement les solutions
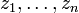 . On cherche donc à exprimer les zi en fonction des ai.
. On cherche donc à exprimer les zi en fonction des ai.Cette démarche s’applique plus généralement si coefficients et solutions prennent leurs valeurs dans un anneau intègre.
Second degré
Article détaillé : Équation du second degré.Pour résoudre une équation du second degré du type ax2 + bx + c = 0 on calcule son discriminant Δ défini par Δ = b2 − 4ac.
Si Δ > 0, alors l’équation a deux racines réelles distinctes x1 et x2, telles que :
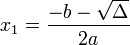
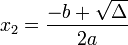 .
.
Si Δ = 0, l’équation a alors une racine réelle double x0, telle que :
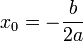 .
.
Si Δ < 0, il n’existe aucune racine réelle au trinôme. Cependant il possède 2 racines complexes conjuguées z1 et
 . Si Δ = (iδ)2, on peut écrire :
. Si Δ = (iδ)2, on peut écrire :Équations se ramenant au second degré
Certaines équations de degré trois ou quatre se ramènent facilement à des équations du second degré. Leur résolution nécessite de connaître la formule de résolution des équations du second degré et les nombres complexes.
Premier exemple : racine(s) évidente(s)
Lorsqu’une équation de degré n admet une solution évidente, on peut factoriser le polynôme associé en un facteur du premier degré et un polynôme de degré n − 1. La résolution de l’équation se ramène donc à celle d’une équation de degré n − 1.
On se propose d’étudier pour quelles valeurs de x la fonction réelle
 , polynomiale de degré 3, s’annule.
, polynomiale de degré 3, s’annule.On remarque tout d’abord que f( − 1) = 0. Donc -1 est une racine du polynôme.
On cherche alors (α,β,γ) tels que
 .
.
On a :
Or deux polynômes sont égaux s’ils sont de même degré et si leurs coefficients respectifs sont égaux deux à deux. Donc :
et
Ainsi,
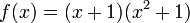 ,
,
et résoudre f(x) = 0 revient à résoudre x + 1 = 0, puisque x2 + 1 > 0. L’unique solution réelle de l’équation est − 1.
Deuxième exemple : équations bicarrées
On se propose de rechercher les racines du polynôme bicarré
(est dit bicarré tout polynôme de la forme
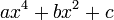 ). Pour cela, nous allons réaliser un changement d’inconnue.
). Pour cela, nous allons réaliser un changement d’inconnue.Posons X = x2, on a alors f(x) = 7X2 + 4X − 3. L’équation du second degré obtenue a pour discriminant Δ = 42 − 4(7)( − 3) = 16 + 84 = 100. Ses solutions sont donc
Ces solutions sont exactement les carrés des solutions de l’équation de départ
 .
.
L’ensemble des racines de f est donc
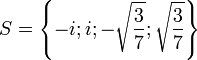 .
.
Troisième exemple, où x ↦ ax + b√x + c
L’objectif est ici d’étudier les solutions de l’équation f(x) = 0, avec
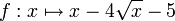 . Cela illustre que certaines équations non polynomiales se ramènent, elles aussi, à des équations polynomiales du second degré.
. Cela illustre que certaines équations non polynomiales se ramènent, elles aussi, à des équations polynomiales du second degré.On pose
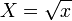 ; on peut donc écrire f(x) = X2 − 4X − 5. On résout alors l’équation f(x) = 0 d’inconnue X : X2 − 4X − 5 = 0 équivaut à (X − 2)2 − 9 = 0. Les solutions sont donc X1 = 5 et X2 = − 1. La solution X2 = − 1 doit être rejetée car le changement de variable
; on peut donc écrire f(x) = X2 − 4X − 5. On résout alors l’équation f(x) = 0 d’inconnue X : X2 − 4X − 5 = 0 équivaut à (X − 2)2 − 9 = 0. Les solutions sont donc X1 = 5 et X2 = − 1. La solution X2 = − 1 doit être rejetée car le changement de variable 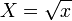 impose
impose  .
.La seule solution possible de f(x) = 0 est donc :
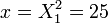
Troisième et quatrième degré
Pour résoudre une équation du troisième ou du quatrième degré, on peut tenter de ramener l’équation à une multiplication d’au moins deux polynômes plus simples (voir ci-dessus).
Jérôme Cardan a résolu certaines équations de degré 3 et a exprimé les racines sous la forme de radicaux. Leonhard Euler a résolu ces équations d’une manière générale en commençant par rendre nul le terme de degré inférieur à celui du terme dominant en cherchant sans succès une méthode générale s’appliquant ensuite aux équations de degré supérieur.
Pour un exposé détaillé de certaines méthodes de résolution voir :
- Méthode de Tschirnhaus (Méthode générale qui peut ne pas aboutir).
- Méthode de Bézout (Méthode générale qui peut ne pas aboutir).
- Méthode de Cardan (Résolution des équations de degré 3).
- Méthode de Sotta (Résolution des équations de degré 3 et généralisation à un degré quelconque sous certaines conditions).
- Méthode de Ferrari (Résolution des équations de degré 4).
- Méthode d'Euler (Résolution des équations de degré 4).
- Méthode de Descartes (Résolution des équations de degré 2 et 4).
Équations de degré supérieur
Article détaillé : Théorème d'Abel (algèbre).Évariste Galois et Niels Henrik Abel ont démontré indépendamment l’un de l’autre que d’une manière générale une équation polynomiale de degré 5 ou plus n’est pas résoluble par radicaux (voir paragraphe Théorie ci-dessus). Un exemple d'équation non résoluble par radicaux est donné dans l'article Groupe alterné. Certaines équations particulières le sont, comme par exemple celles associées aux polynômes cyclotomiques d'indice 5 ou 17.
Charles Hermite a en revanche démontré que les équations polynomiales de degré 5 sont résolubles à l’aide des fonctions elliptiques.
Voir en particulier :
Voir aussi
Articles connexes
- Équation
- Équation du second degré | Équation cubique | Équation quartique | Équation quintique
- Histoire des polynômes
- Polynôme formel | Fonction polynôme
- Nombre constructible | Nombre complexe
- Fonction elliptique
- Théorie de Galois
- Relations entre coefficients et racines
- Racine d'un polynôme
- Portail des mathématiques
Catégorie : Équation polynomiale
Wikimedia Foundation. 2010.

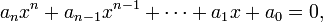
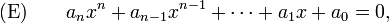
![P = a_n X^n + a_{n - 1} X^{n - 1} + \cdots + a_1 X + a_0 \quad \in \mathbb K[X],](/pictures/frwiki/97/a6777d8338fc371c90e7aaa1d0e31fd6.png)