- Representations du groupe symetrique d'indice quatre
-
Représentations du groupe symétrique d'indice quatre
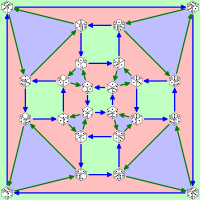 Graphe de Cayley du groupe symétrique d'indice quatre en tant que groupe de rotations d'un dé standard.
Graphe de Cayley du groupe symétrique d'indice quatre en tant que groupe de rotations d'un dé standard.
En mathématiques les représentations du groupe symétrique d'indice quatre noté S4 sont un exemple d'application de la théorie des représentations d'un groupe fini.
Sur le corps des nombres complexes, il existe cinq représentations irréductibles du groupe symétrique d'indice quatre, la représentation triviale, celle correspondant à la signature, une d'ordre deux et deux d'ordre trois. L'une s'obtient de l'autre par produit tensoriel avec la représentation correspondant à la signature. Une des représentations de degré trois correspond aux rotations linéaires laissant invariant un cube.
L'analyse des représentations de S4 est une illustration des concepts comme le théorème de Maschke, les caractères, la représentation régulière, les représentations induites et la réciprocité de Frobenius.
Sommaire
Histoire
L'histoire des représentations du groupe symétrique d'indice quatre, avec celui d'ordre cinq et des groupes alternés associé joue un rôle particulier pour la théorie des caractères. Le 12 avril 1896 est la date de naissance[1] généralement considérée de cette théorie. Dans une série de lettres adressées à Dedekind (1831-1916), Frobenius (1849 - 1917) analyse les représentations des groupes cités et présente les fondements qu'il développe pendant les années à venir.
Si les méthodes sont différentes de celles maintenant utilisées, Frobenius utilise en effet comme outil essentiel les déterminants de groupes tombés maintenant en désuétude, les bases de la théorie sont esquissées. Elle se développe rapidement, Heinrich Maschke (1853 1908) démontre le théorème portant maintenant son nom[2] trois ans plus tard. En 1911, William Burnside (1852-1927) publie la seconde édition du livre[3] encore de référence contenant toutes les techniques utilisées dans cet article.
Caractère
Article détaillé : Représentations d'un groupe fini.Les représentations des groupes finis possèdent une propriété simplifiant largement leur analyse, elles sont toutes somme directe de représentation irréductibles. Il suffit donc de connaître toutes les représentations irréductibles pour savoir construire toutes les représentations.
Classe de conjugaison
Article détaillé : Classe de conjugaison.Les classes de conjugaison ont un rôle important pour les représentations, il existe en effet exactement autant de représentations irréductibles qui ne sont pas équivalentes que de classes de conjugaison.
Comme le montre l'article Groupe symétrique, Les conjuguées d'un élément de S4 sont les permutations dont la décomposition en produit de cycles à supports disjoints a la même structure que celle de σ : même nombre de cycles de chaque longueur.
Dans le cas de S4, on en trouve exactement cinq : l'identité, les transpositions de la forme (ab) au nombre de six, les cycles de longueurs trois de la forme (abc) au nombre de huit, les paires de transpositions (ab)(cd) au nombre de trois et les cycles de longueur quatre de la forme (abcd) au nombre de six. On retrouve bien les vingt-quatre éléments du groupe répartis en cinq classes de conjugaison.
Orthogonalité
Article détaillé : Caractère d'une représentation d'un groupe fini.Le caractère d'une représentation correspond à l'application de S4 dans C l'ensemble des nombres complexes, qui à un élément s associe la trace de l'automorphisme associé à s par la représentation. Les caractères possèdent des propriétés fortes : ils forment une base de l'espace des fonctions centrales à valeur dans C. Une fonction centrale est une fonction définie sur le groupe et constante sur les classes de conjugaisons. De plus, pour le produit hermitien suivant la famille des caractères irréductibles est une base orthonormale :
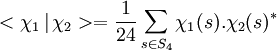
Ici, χi désignent des fonctions centrales à valeur dans C et a* désigne le conjugué du nombre complexe a.
Un caractère est irréductible si et seulement si sa norme est égale à un, deux représentations irréductibles sont isomorphes si et seulement si leur produit hermitien est égal à un, dans le cas contraire, le produit est nul. De plus, si di pour i variant de 1 à 5 désigne les degrés des différentes représentation irréductibles, on dispose de l'égalité suivante :
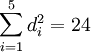
Comme les di sont des entiers naturels, on a nécessairement, les 5 nombres suivants : 1;1;2;3;3.
Il y a donc 2 représentations irréductibles de dimension 1 qui ne sont pas équivalentes, une représentation irréductible de degré 2 et deux représentations irréductibles de dimension 3 qui ne sont pas équivalentes.
Les deux représentations irréductibles immédiates sont :
- La représentation triviale t qui à chaque élément du groupe associe un.
- La représentation qui à σ associe la signature. Pour ces deux représentations, on obtient la table des caractères :
Car. irr. 1 (ab) (abc) (ab)(cd) (abcd) t 1 1 1 1 1 σ 1 -1 1 1 -1 Comme S4 est un groupe symétrique, il existe une représentation naturelle (V, ρ) de ce groupe : soit V un espace de dimension quatre sur C, p une permutation de S4, (ei) pour i variant de 1 à 4 une base de V alors l'image de ρ(p) de la base (ei) est la famille (ep(i)). Chaque élément de S4 possède comme image par ρ un automorphisme de matrice une matrice de permutation d'ordre quatre. La trace de ρ(s) si s est un élément du groupe correspond au nombre de vecteur de la base laissé invariant, si l'ordre des classes de conjugaison est le même que celui du tableau, on obtient le caractère (4, 2, 1, 0, 0). Le sous-espace vectoriel de dimension un engendré par le vecteur somme des éléments de la base est stable et correspond à la représentation irréductible triviale. Comme toute représentation est somme directe de représentations irréductibles, il existe une représentation, correspondant à la représentation naturelle à laquelle a été retranchée la représentation triviale. On obtient une représentation φ1 de caractère (3, 1, 0, -1, -1) obtenu en retranchant le caractère de la représentation triviale à celle de la représentation naturelle. La représentation obtenue est de dimension 3 et on vérifie grâce au caractère qu'elle est irréductible :

Le produit tensoriel de deux représentations est une représentation de caractère le produit des caractères, en conséquence si φ2 est le produit tensoriel de φ1 et de σ, on obtient représentation de caractère (3, -1, 0, -1, 1). Un calcul analogue à celui appliqué à φ1 montre qu'il est irréductible. On a donc déterminé la seconde représentation irréductible de dimension 3, et toujours grâce aux caractères, on vérifie qu'elles ne sont pas équivalentes.
Il manque donc une représentation irreductible de degré deux. Utilisons la représentation régulière pour déterminer le dernier. La représentation régulière est somme directe de toutes les représentations irréductibles et il existe autant de copies d'une représentation irréductible donnée que la dimension de cette représentation irréductible. De plus le caractère de la représentation régulière est (24, 0, 0, 0, 0). Par soustraction, on obtient le caractère de θ : (2, 0, -1, 2, 0). Le tableau des caractères est donc :
Car. irr. 1 (ab) (abc) (ab)(cd) (abcd) t 1 1 1 1 1 σ 1 -1 1 1 -1 θ 2 0 -1 2 0 φ1 3 1 0 -1 -1 φ2 3 -1 0 -1 1 Représentation
L'objectif du paragraphe est la détermination effective des différentes représentations. Pour celle de dimension un, c’est-à-dire t et σ, elles se confondent avec leur caractère, elles sont donc de facto déterminées.
Le groupe S4 est engendré par les transpositions, il n'est donc nécessaire que de déterminer les représentations que pour elles. De plus, on remarque que les transpositions (12), (23), (34) engendrent toutes les transpositions, donc le groupe entier. Dans la suite de paragraphe, les représentations ne sont exprimées que sur ces trois éléments. Les autres se déduisent par produits des automorphismes précédents.
Représentation de θ
Article détaillé : Représentations du groupe symétrique d'ordre trois.Considérons le groupe H formé des quatre éléments 1 et les trois éléments de la classe de conjugaison de la forme (ab)(cd). On vérifie aisément que c'est un sous groupe, de plus comme il est formé par l'union de deux classes de conjugaison, il est distingué. Considérons alors le groupe S4/H. C'est un groupe d'ordre six, isomorphe à S3. Soient s la surjection canonique de S4 dans S4/H et (W, θ2) la représentation irréductible de S3 d'ordre deux (cf Représentations du groupe symétrique d'ordre trois), définissons alors θ comme étant égal à θ2os. La composition de morphismes étant un morphisme, (W, θ) est une représentation. Déterminons son caractère : il existe trois transpositions dans S3 correspondant à douze valeurs dans S4, à savoir les transpositions et les permutations circulaires du type (abcd). Il existe deux éléments d'ordre trois dans S3 correspondant à la classe (abc) dans S4, enfin la classe de l'élément neutre est composé du sous-groupe H. On en déduit que cette représentation possède bien le caractère recherchée et :
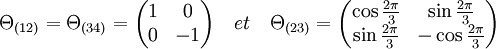
La représentation possède bien le caractère recherché. Elle est de degré deux, le caractère est donc bien égal à deux pour la classe de conjugaison associée à l'identité, composée par le groupe H. Les transpositions représentent trois images par la représentation, chaque classe contient deux transpositions et deux cycles d'ordre quatre, la valeur associée au caractère est égale à zéro. Enfin, les cycles d'ordre trois sont formés par les éléments de la classe (abc), elle engendre deux images par la représentation.
La représentation est alors celle du groupe des isométries du triangle. Elle n'est pas fidèle et chaque automorphisme de la représentation possède quatre antécédents. La figure de droite illustre cette représentation. On a nommé les trois sommets du triangle au moyen des trois étiquettes 1x2 + 3x4, 2x3 + 1x4 et 1x3 + 2x4. Une permutation de S4 agit directement sur les chiffres de chaque étiquette. Ainsi,la transposition (12) laisse le sommet 1x2 + 3x4 invariant mais permute les deux sommets 2x3 + 1x4 et 1x3 + 2x4. On pourra vérifier que l'action de cette transposition est identique à celle de la transposition (34) ou celle des permutations circulaires (1324) ou (1423). Une telle action du groupe S4 est utilisée pour résoudre les équations du quatrième degré.
Représentation de φ
Considérons la représentation naturelle, celle définie par le fait que le groupe S4 opère par permutation sur une base (ei) d'un espace de dimension quatre. Le paragraphe précédent montre qu'une telle représentation possède le caractère de φ1, obtenue en considérant un sous-espace stable par l'action de S4, et supplémentaire de la droite engendrée par la somme des ei.
Si l'on considére la base (ui) définie par la matrice de passage P de (ui) dans (ei), on obtient comme matrice de la représentation φ1 dans la base constituée des trois derniers vecteurs ui :

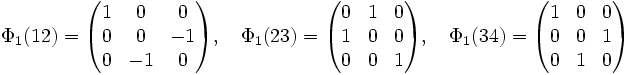
Les images par Φ1 des permutations de S4 sont alors les matrices orthogonales laissant globalement invariant le tétraèdre régulier de sommets M1 = (-1,-1,-1), M2 = (-1,1,1), M3 = (1,-1,1) et M4 = (1,1,-1), et permutant ces quatre sommets. Les transpositions (ab) correspondent à des réflexions, les permutations (ab)(cd) à des demi-tours, les permutations (abc) à des tiers de tour, et les permutations (abcd) aux composées d'un quart de tour et d'une réflexion.
Pour obtenir la représentation φ2, il suffit de multiplier la représentation matricielle de φ1 par le caractère σ. Elle est généralement obtenue avec les générateurs suivant: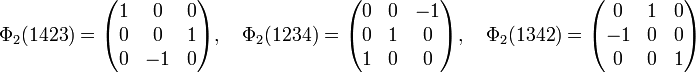
On reconnait trois rotations laissant invariant le cube, la première suivant l'axe des x, la deuxième suivant l'axe des y et la troisième suivant celui des z.
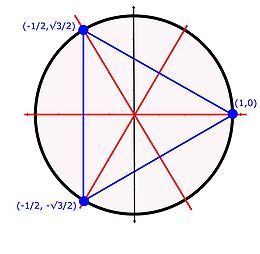
La figure au début du paragraphe illustre l'interprétation géométrique de la représentation φ2, l'image de (1423) est celle représentée par la flèche rouge, celle de (1234) par la bleue et celle de (1342) par la verte. Les rotations du cube permutent alors les quatre diagonales du cube ou, de manière équivalente, les quatre paires de sommets opposés.
On peut également visualiser l'action de ces permutations de la façon suivante. Les rotations laissant invariant le cube laissent également invariant le cuboctaèdre. Les transpositions (ab) correspondent à des demi-tours d'axes passant par deux sommets opposés, les permutations (ab)(cd) à des demi-tours d'axes passant par les centres des carrés, les permutations (abc) à des tiers de tour d'axes passant par les centres des triangles, et les permutations (abcd) à des quarts de tour d'axes passant par les centres des carrés. Les rotations de la représentation permutent alors les quatre paires de triangles opposés.
Notes et références
Notes
- ↑ C. W. Curtis Representation theory of finite groups, from Frobenius to Brauer Math. Intelligencer p 48-57 1992
- ↑ Heinrich Maschke Beweiss des Satzes, dass diejenigen endlichen linearen Substitutionesgruppen, in welchen einige durchgehends verschwindende Coefficienten auftenen intransitiv sind 1899
- ↑ William Burnside Theory of Groups of Finite Order second edition Dover Publications Réédition de 2004
Liens externes
- (fr) Cours de représentation des groupes finis par M. Broué de l'université de Paris VII
- (fr) Représentation linéaire des groupes finis, une introduction par D. Ferrand de l'université de Renne
- (fr) Représentations linéaires des groupes finis Par Gabriel Peyré
Références
- Jean-Pierre Serre, Représentations linéaires des groupes finis [détail des éditions]
- (en) Marshall Hall, The theory of groups [détail des éditions]
- Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808)[détail des éditions]
- N. Bourbaki Algèbre, Chapitre VIII Paris, Hermann 1958
- Portail des mathématiques
Catégorie : Théorie des représentations
Wikimedia Foundation. 2010.