Algebre d'un groupe fini

Algèbre d'un groupe fini

En mathématiques, l' algèbre d'un groupe fini s'inscrit dans le cadre de la théorie des représentations d'un groupe fini.

Une algèbre d'un groupe fini est la donnée d'un groupe fini, d'un espace vectoriel de dimension l'ordre du groupe et d'une base indexée par le groupe. La multiplication des éléments de la base est obtenue par la multiplication des index à l'aide de la loi du groupe, elle est prolongée sur toute la structure par linéarité. Une telle structure est une algèbre semi-simple, elle dispose de toute une théorie dont le théorème d'Artin-Wedderburn est le pilier.

Cette approche apporte un nouvel angle d'analyse pour la représentation des groupes. Elle permet d'établir par exemple, la formule de réciprocité de Frobenius, le théorème d'Artin ou par exemple celui de Brauer.

Sommaire

1 Introduction
- 1.1 Nature de la démarche
- 1.2 Applications
2 Définitions
- 2.1 Algèbre d'un groupe
- 2.2 G-module
3 Propriétés
4 Applications
5 Notes et références
- 5.1 Liens externes
- 5.2 Références

Introduction

Nature de la démarche

L'objectif est l'étude des représentations d'un groupe fini G sous un angle particulier. Dans un premier temps, une unique représentation est étudiée, la représentation régulière. L'ensemble de départ est linéarisé, c’est-à-dire qu'il est identifié à l'espace vectoriel sur le corps K de la représentation, le groupe devenant la base canonique de l'espace. Le morphisme de groupe de G dans le groupe linéaire de l'espace vectoriel est prolongé par linéarité. On obtient une structure d'algèbre associative sur un corps commutatif, noté K[G] (pour les notations, voir l'article polynôme en plusieurs indéterminées). Avec les caractères, cette approche est l'un des deux piliers de la théorie des représentations.

Le théorème de Maschke démontre que si l'ordre du groupe n'est pas un multiple de la caractéristique du corps K, l'algèbre est semi-simple. Cette structure, objet d'une vaste théorie, permet la démonstration de résultats variés grâce à ses nombreux théorèmes. L'un des plus importants est sans doute celui d'Artin-Wedderburn, il indique que, si le corps est algébriquement clos, ou si le polynôme X^g - 1 est scindé, l'algèbre est isomorphe à une somme directe d'algèbres des endomorphismes sur des K-espaces vectoriels de dimension finis. Ici g désigne l'ordre du groupe.

L'algèbre d'un groupe opère sur toutes les représentations, il suffit de prolonger le morphisme de groupe par linéarité. On obtient une structure de module où l'anneau K[G] opère sur l'espace vectoriel de la représentation. Une telle structure se nomme G-module. Il existe une équivalence stricte entre la notion de G-module et celle de représentation de G.

Applications

L'essentiel des premiers résultats de la théorie des représentations est une conséquence directes des propriétés générales des algèbres semi-simples. On peut démontrer le caractère fini du nombre de représentations irréductibles, ou l'égalité entre l'ordre du groupe et la somme des carrés des dimensions des représentations irréductibles. Il est vrai que ces propriétés se démontrent souvent facilement à l'aide des caractères, sans l'adjonction d'une théorie riche mais parfois complexe. En revanche, certains de ces résultats se démontrent de manière plus aisée avec une approche par les algèbres semi-simples, c'est le cas du critère de réciprocité de Frobenius.

Il existe des éléments propres aux algèbres qui sont indispensables à la théorie des représentations. Le centre de l'algèbre K[G] est naturellement une extension abélienne commutative du corps K. Il est possible d'utiliser la notion d'entier algébrique. Cette remarque permet d'introduire une arithmétique, qui s'avère incoutournable. Elle est utilisée dans cet article pour démontrer que toute représentation irréductible possède un degré divisant l'ordre du groupe.

Dans le cas où g est un multiple de la caractéristique du groupe, la propriété fondamentale des caractères, à savoir l'aspect orthonormal des caractères irréductibles disparait. L'algèbre du groupe perd aussi sa semi-simplicité. En revanche la théorie des anneaux semi-simples et particulièrement le concept de radical de Jacobson permet d'élucider la nature des représentations.

Définitions

Algèbre d'un groupe

Article détaillé : Algèbre semi-simple.

Les notations suivantes sont utilisées dans tout l'article. G désigne un groupe fini noté multiplicativement, son élément neutre est noté 1 et son ordre g. K est un corps commutatif de caractéristique soit nulle soit première avec g.

La K-algèbre du groupe G, noté K[G] est l'espace vectoriel des combinaisons linéaires formelles des éléments de G, il est muni de la multiplication suivante :

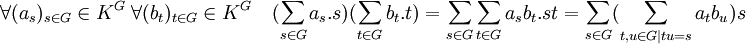
$\forall (a_s)_{s\in G}\in K^G \; \forall (b_t)_{t\in G}\in K^G \quad (\sum_{s\in G} a_s.s)(\sum_{t\in G} b_t.t)= \sum_{s\in G}\sum_{t\in G} a_sb_t.st =\sum_{s\in G} (\sum_{t,u \in G \mid tu=s} a_t b_u ) s$

La construction rigoureuse d'une telle algèbre est présentée dans l'article polynôme en plusieurs indéterminées, dans le paragraphe sur l'algèbre d'un monoïde. Une telle structure bénéficie de la propriété suivante :

La structure K[G] est celle d'une algèbre associative sur un corps.

Quelques définitions sont nécessaires, elle concerne les algèbres en général :

Une algèbre est dite simple si les seuls idéaux bilatères sont {0} et l'algèbre elle-même.
Un idéal est dit facteur direct si et seulement s'il existe un idéal bilatère sous-espace supplémentaire.
Une algèbre est dite semi-simple si et seulement si toute sous-algèbre simple est facteur direct.

Une algèbre de groupe possède la propriété suivante appelée théorème de Maschke :

Si l'ordre du groupe n'est pas un multiple de la caractéristique du corps K, alors l'algèbre du groupe est semi-simple.

Démonstration

La structure K[G] est celle d'une algèbre.

L'associativité de la multiplication interne est la conséquence de celle du groupe et de la multiplication du corps :

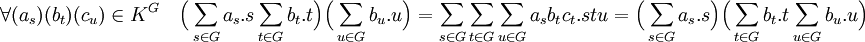
$\forall (a_s)(b_t)(c_u)\in K^G \quad \Big(\sum_{s\in G} a_s.s\sum_{t\in G} b_t.t\Big)\Big(\sum_{u\in G} b_u.u\Big)=\sum_{s\in G}\sum_{t\in G}\sum_{u\in G}a_sb_tc_t.stu= \Big(\sum_{s\in G} a_s.s\Big)\Big(\sum_{t\in G} b_t.t\sum_{u\in G} b_u.u\Big)$

La distributivité de la multiplication interne par rapport à l'addition est la conséquence de celle du corps et de l'espace vectoriel. Le calcul suivant démontre la distributivité à droite, celle de gauche est analogue :

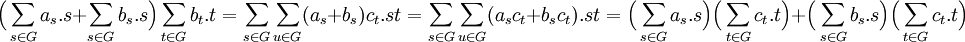
$\Big(\sum_{s\in G} a_s.s + \sum_{s\in G} b_s.s\Big)\sum_{t\in G} b_t.t=\sum_{s\in G}\sum_{u\in G}(a_s+b_s)c_t.st= \sum_{s\in G}\sum_{u\in G}(a_sc_t+b_sc_t).st= \Big(\sum_{s\in G} a_s.s\Big)\Big(\sum_{t\in G} c_t.t\Big) + \Big(\sum_{s\in G} b_s.s\Big)\Big(\sum_{t\in G} c_t.t\Big)$

La compatibilité de la multiplication de l'anneau est de l'espace vectoriel est une conséquence de celle de l'espace vectoriel :

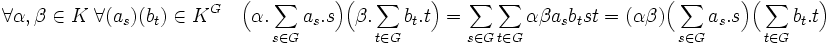
$\forall \alpha,\beta \in K\;\forall (a_s)(b_t)\in K^G \quad \Big(\alpha.\sum_{s\in G} a_s.s\Big)\Big(\beta.\sum_{t\in G} b_t.t\Big)= \sum_{s\in G}\sum_{t\in G}\alpha\beta a_s b_t st =(\alpha\beta)\Big(\sum_{s\in G} a_s.s\Big)\Big(\sum_{t\in G} b_t.t\Big)$

G-module

Article détaillé : Module semi-simple.

Un module sur l'anneau de l'algèbre du groupe K[G] est appelé un G-module.

Le théorème de Maschke démontre qu'un G module est semi-simple. En conséquence il bénéficie de la propriété suivante :

En dimension finie, un module est semi-simple si et seulement si elle est somme directe de sous-module simples.

La démonstration est donnée dans l'article associé. Cette propriété se transpose immédiatement à l'algèbre de groupe.

La structure multiplicative de l'anneau restreint à GxV si V désigne le G module définit une représentation. Réciproquement tout morphisme d'une représentation se prolonge par linéarité sur K[G]. En conséquence, il existe donc une équivalence stricte entre la notion de G-module et celle de représentation.

Soit V₁ et V₂ deux G-modules, la notation hom_K^G(V₁, V₂) désigne la K-algèbre des morphismes de G-module de V₁ dans V₂.

Un tel morphisme φ vérifie les propriétés suivantes:

$\forall \alpha ,\beta \in \mathbb K \quad \forall a,b \in V_1 \quad \forall k \in \mathbb K[G]\quad \varphi (\alpha a + \beta b) = \alpha \varphi (a) + \beta \varphi (b) \quad et \quad \varphi (k.a) = k. \varphi (a) \quad$

Propriétés

Représentation régulière

Article détaillé : Représentation régulière.

On suppose dans ce paragraphe que la caractéristique de K est soit nulle soit première avec g et K est alors algébrique. On suppose de plus que le polynôme X^g - 1 est scindé.

La représentation régulière correspond à celle de l'algèbre de groupe. Par défaut, elle ne dispose pas d'une multiplication interne mais d'un morphisme de groupe de G dans le groupe linéaire de l'espace vectoriel V de dimension g. Une analyse de la représentation apporte un éclairage important sur K[G]. En particulier, on démontre que toutes les représentations irréductibles sont isomorphes à un G-module, et plus précisément :

Soient (V, ρ) la représentation régulière de G et (W, σ) une représentation irréductible de G de degré d, il existe exactement d sous espaces invariants V_i de V, d'intersection nulle deux à deux, tel que la restriction ρ_i de ρ à V_i soit une représentation isomorphe à (W, σ).

La démonstration est donnée dans l'article associé.

L'analyse de l'algèbre du groupe permet de comprendre plus profondément la structure de la représentation régulière. Une définition est néanmoins nécessaire :

Un espace somme directe de copies d'un G-module simple est dit isotypique. La somme directe de toutes les copie d'un G-module simple est appelée composante isotypique du module simple dans le G-module.

La représentation régulière, isomorphe à K[G] est un module semi-simple de longueur fini. K[G] est donc somme directe d'un nombre fini de sous-modules, correspondant à des représentations irréductibles. Soit (S_i) une famille maximale de sous-modules non isomorphes deux à deux. Cette famille est finie et l'on note h son cardinal. La théorie des modules semi-simples indique que la composante isotypique de S_i ne contient que des représentations irréductibles isomorphes à S_i. Si d_i est le nombre de copies de S_i contenues dans une somme directe égal à la composante isotypique, alors celle-ci est notée 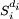$\scriptstyle S_i^{d_i}$ . On dispose de l'isomorphisme suivant :

$\mathbb K[G] \; \simeq \; \bigoplus_{i=1}^h S_i^{d_i}$

La démonstration est donnée dans l'article Module semi-simple.

Théorème d'Artin-Wedderburn

Article détaillé : Théorème d'Artin-Wedderburn.

Avec les notations du paragraphe précédent, le théorème d'Artin-Wedderburn indique que :

Il existe un isomorphisme d'algèbres entre K[G] et la somme directe des h algèbres L_K(S_i) des endomorphismes de V_i en tant qu'espaces vectoriels sur K.

$\mathbb K[G] \; \simeq \; \bigoplus_{i=1}^h \mathcal L_{\mathbb K}(S_i)$

Cet isomorphisme montre par exemple que si (d_i) est la famille du paragraphe précédent, c'est aussi la dimension de S_i, on retrouve l'égalité suivante :

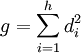
$g=\sum_{i=1}^h d_i^2\;$

Il est toute fois possible de déterminer l'isomorphisme directement, sans utiliser le théorème. La démonstration est donnée dans la boîte déroulante.

Démonstration

Construction de l'isomorphisme :

Soit k un entier entre 1 et h et ψ_k une représentation irréductible de S_k, c’est-à-dire un morphisme de groupe entre G et GL(S_k). Soit φ_k le prolongement de ψ_k par linéarité à K[G] dans L(_k) et enfin φ l'application de K[G] dans la somme directe des L(S_i) qui à x associe le produit des φ_i(x) pour i variant de 1 à h. L'application φ est un morphisme d'algèbre, montrons qu'il est bijectif.

Surjectivité :

Il suffit de montrer que φ_k est surjectif si k est un entier entre 1 et h. Soit (f_nm^k) la matrice de φ_k dans une base quelconque de S_k. Montrer que φ_k est surjectif revient à montrer que si s décrit le groupe G, alors φ_k(s) est une famille génératrice de L(S_k). L'espace généré par les φ_k(s) est de dimension celle de la famille des fonctions de K^G qui à s associe f_nm^k(s) correspondant à d^k au carré coefficients de la représentation matricielle. Or le lemme de Schur (cf corolaire 4) montre la relation suivante :

$\forall n,m,n',m' \in [1,d] \quad \frac{1}{g}\sum_{s\in G} f_{nm}^k(s). f_{n'm'}^k(s^{-1}) = \frac{1}{d}\delta_{nm'}\delta_{n'm}$

Ce qui exprime l'orthogonalité des différents coefficients pour une forme bilinéaire. La famille des coefficients est libre, donc de rang le carré de d _k si ce nombre désigne ici la dimension de S_k. La famille φ_k(s) est donc de rang la dimension de L(S_k), ce qui montre la surjectivité.

Injectivité :

Les dimensions de K[G] et du produits d'algèbres d'endomorphismes sont les mêmes et φ est surjective, ce qui démontre l'injectivité.

Centre de l'algèbre

Article détaillé : Action par conjugaison.

Un anneau important de l'algèbre de groupe est le centre D de K[G], c’est-à-dire l'ensemble des éléments commutant avec tous les éléments de l'algèbre. La théorie des algèbres semi-simples indique que c'est un anneau isomorphe à K^h où h désigne le nombre maximal de représentations irréductibles non isomorphes deux à deux. Cette anneau est composée de la somme directe des homothéties dans L(S_i) si i varie de 1 à h.

$\mathbb K[G] \; \simeq \; \bigoplus_{i=1}^h \mathcal L_{\mathbb K}(S_i)\quad et \quad \mathbb D = \bigoplus_{i=1}^h \{f \in \mathcal L_{\mathbb K}(S_i) \; / \; \exists \lambda_i \in \mathbb K \quad f = \lambda_i.Id\}$

Dans le cas d'une algèbre de groupe, il est possible de déterminer les éléments du centre par leur décomposition dans la base canonique (e_s) où s décrit G. On obtient la proposition suivante :

Soit c une classe de conjugaison et d_c la somme des éléments de la base canonique indexés par les éléments de c. Le centre de K[G] est l'espace vectoriel engendré par les éléments d_c lorsque c parcourt l'ensemble des classes de conjugaison.

Le nombre h de représentations irréductibles différentes est donc égal au nombre de classes de conjugaison. Cette analyse fournit des résultats complémentaires de ceux obtenus par les caractères. Cette théorie indique que les caractères forment une base orthonormale de l'ensemble des fonctions centrales. La relation entre les deux est établie par la proposition suivante, si C désigne l'ensemble des classes de conjugaison :

L'application φ défini ci-dessous, de l'espace des fonctions centrales K^C dans le centre de K[G] est un isomorphisme d'algèbre sur K.

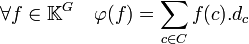
$\forall f \in \mathbb K^G \quad \varphi (f) = \sum_{c \in C} f(c).d_c$

Pour cette raison, on identifie généralement le centre de l'algèbre et l'ensemble des fonctions centrales.

Le centre peut être vu de trois manières différentes, soit comme l'espace des fonctions centrales, soit comme une somme directe S d'algèbres d'endomorphismes d'espaces vectoriels L_K(S_i), soit comme un sous-espace vectoriel de K[G]. Si φ désigne l'isomorphisme de K[G] dans S, la relation entre les trois visions est la suivante, si χ_i est le caractère de S_i et d_i la dimension de S_i :

Soit u un élément du centre de K[G] et u_s ses coordonnées dans la base canonique, l'image de u par φ est une somme directe d'homothéties sur S_i de rapport λ_i avec :

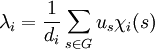$\lambda_i = \frac{1}{d_i}\sum_{s \in G} u_s \chi_i(s)$

Démonstrations

Soit c une classe de conjugaison et d_c la somme des éléments indéxés par c. Le centre de K[G] est l'espace vectoriel engendré par les éléments d_c lorsque c parcourt l'ensemble des classes de conjugaison.

Montrons que d_c est élément du centre :

Tout automorphisme intérieur restreint à c est une permutation et donc laisse d_c invariant. En conséquence, si s est un élément de G, sd_cs^-1 = d_c ou encore sd_c = d_cs, ce qui démontre que l'espace engendré par les d_c est inclus dans le centre.

Réciproquement, montrons que le centre est combinaison linéaire des e_c :

Il suffit de montrer que, si x est un élément du centre de K[G], son écriture comme combinaison linéaire des vecteurs de la base G possède des coefficients égaux pour deux éléments s et t conjugués. Soit Aut_u un automorphisme intérieur tel que son image de s soit égal à t. Soit p la projection sur l'espace vectoriel engendré par s et t parallèlement à l'espace vectoriel engendré par les autres éléments de G. Dire que x est un élément du centre revient à dire qu'il est stable par tous les automorphismes intérieurs, en particulier poAut_u(x)=p(x). Soit λ_a le coefficient de x pour le vecteur a de la base G, alors p(x) est égal à λ_ss + λ_tt, et il existe un élément v de G tel que poAut_u(x) soit égal à λ_vs + λ_st. L'égalité poAut_u(x)=p(x) montre que λ_ss et λ_tt sont égaux, ce qui termine la démonstration.

Soit u un élément du centre de K[G] et u_s ses coordonnées dans la base indicée par G, l'image de u par φ est une somme directe d'homothéties sur S_i de rapport λ_i avec :

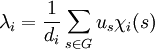
$\lambda_i = \frac{1}{d_i}\sum_{s \in G} u_s \chi_i(s)$

Si φ_i désigne la composante de φ dans L_K(S_i), par linéaité, φ_i(u) s'écrit de la manière suivante :

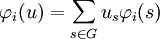
$\varphi_i(u)=\sum_{s \in G} u_s\varphi_i(s)$

La trace de l'application est égale à d_i fois le rapport de l'homothétie, et donc, si Tr(φ_i(u)) désigne la trace de φ_i(u) alors elle est égale à d_i.λ_i et donc :

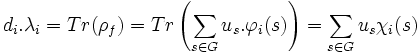
$d_i.\lambda_i= Tr(\rho_f)=Tr\left(\sum_{s \in G} u_s.\varphi_i(s)\right)= \sum_{s \in G} u_s \chi_i(s)$

Orthogonalité

La complémentarité des deux approches, par les caractères et par l'algèbre du groupe s'applique aussi sur les propriétés d'orthogonalité. Soit (V₁, ρ¹) et (V₂, ρ²) deux représentations de G :

Si χ₁ et χ₂ désigne les caractères de ρ¹ et ρ² et si les représentations (V₁, ρ¹) et (V₂, ρ²) sont considérées comme des G-module, alors l'égalité suivante est vérifiée :

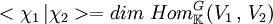
$<\chi_1\, | \chi_2>=dim \; Hom_{\mathbb K}^G (V_1\, ,\, V_2)\;$

En utilisant les notations précédentes, notons :

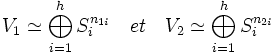
$V_1 \simeq \bigoplus_{i=1}^h S_i^{n_{1i}}\quad et \quad V_2 \simeq \bigoplus_{i=1}^h S_i^{n_{2i}} \;$

Le lemme de Schur démontre que dim Hom_K^G (S_i, S_j) = δ_ij si i et j sont des entiers compris entre 1 et h et δ_ij désigne le symbole de Kronecker. On en déduit :

$dim \; Hom_{\mathbb K}^G (V_1\, ,\, V_2)=dim \; Hom_{\mathbb K}^G \Big(\bigoplus_{i=1}^h S_i^{n_{1i}}\, ,\, \bigoplus_{j=1}^h S_j^{n_{2j}}\Big)=\sum_{ij \in [1,h]} n_{1i}.n_{2j}dim \; Hom_{\mathbb K}^G (S_i\, ,\, S_j)=\sum_{i=1}^h n_{1i}.n_{2i} \;$

La propriété d'orthonormalité des caractères irréductibles permet de conclure.

Applications

Réciprocité de Frobenius

Article détaillé : réciprocité de Frobenius.

Un bon exemple d'utilisation de la structure d'algèbre de groupe est donné par le critère de réciprocité de Frobenius. Il concerne un mode de construction de G-module appelé représentation induite. Soit H un sous-groupe de G et W un K[H]-module. Alors la structure suivante est le G-module induit par W :

$V\simeq K[G]\otimes_{K[H]}W \;$

La représentation induite correspond, à une extension des scalaires K[H] à l'anneau K[G] sur le H-module W. Dans le cas où H est un sous-groupe normal de G, le G-module induit est l'équivalent d'un produit semi-direct.

Le critère de réciprocité de Frobenius est une méthode simple pour calculer le produit hermitien du caractère d'un module induit. Si ψ désigne le caractère de la représentation θ issus du H-module W et χ celui d'une représentation ρ de G, si Ind ψ désigne le caractère d'une représentation induite, c’est-à-dire la représentation associée au module induit et Res χ le caractère de la restriction de ρ à H, alors :

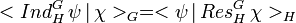
$<Ind_H^G\,\psi\,|\,\chi>_G=<\psi\,|\,Res_H^G\,\chi>_H \;$

Elle se démontre en établissant un isomorphisme entre les deux structures de morphismes de K-algèbre associée, l'égalité des dimensions permet de conclure.

Entier algébrique

Article détaillé : Entier algébrique.

Le centre de K[G] est un anneau commutatif sur le corps K, une extension des rationnels. En conséquence, il est possible de parler d' entier algébrique sur cet ensemble. Cet approche est largement utilisée pour l'analyse de l'algèbre d'un groupe fini, ce paragraphe est un exemple. Notons c les classes de conjugaisons et d_c la somme des éléments de c.

Soit u un élément du centre de K[G] tel que toutes ses coordonnées dans la base (d_c) soit entières (au sens algébrique) sur K, alors u est un entier algébrique.

Comme u est combinaison linéaire à coefficients dans les entiers algébriques des valeurs d_c, il suffit de montrer que ces valeurs sont des entiers algébriques. Soit a et b deux classes de conjugaisons, d_ad_b est combinaison linéaire à coefficients entiers des d_c, en conclusion le Z-module est de type fini, ce qui montre que la famille des d_c est composée d'entiers algébriques. Or, u est combinaison linéaire à coefficients entiers algébriques d'entiers algébriques, ce qui démontre le résultat.

Avec les notations du paragraphe précédent, on dispose de la propriété :

Soit u un élément du centre de K[G] tel que toutes ses coordonnées soit entières (au sens algébrique) sur K, alors le nombre suivant est un entier algébrique.

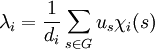
$\lambda_i = \frac{1}{d_i}\sum_{s \in G} u_s \chi_i(s)$

Considérons l'image de u par φ_i, φ_i(u) est un élément du centre de L(S_i), et φ_i est un morphisme d'algèbre. En conséquence φ_i(u) est un entier algébrique du centre de L(S_i), c’est-à-dire de l'espace des homothéties de S_i, isomorphe au corps K. Le rapport de l'homothétie est donc un entier algébrique de K.

On en déduit la propriété suivante :

Le degré d_i d'une représentation irréductible divise l'ordre g du groupe.

Considérons l'élément u égal à la somme si s décrit G des éléments χ_i(s_-1).s, le caractère d'un élément de s est la trace d'un endomorphisme admettant X^g - 1 comme polynôme annulateur. La trace est donc somme de racines g-ième de l'unité est donc à valeur dans les entiers algébriques. La fonction χ_i est un caractère donc une fonction centrale de G, ceci démontre que u est bien un élément du centre de G à coefficients dans la base G donc entiers algébriques. La proposition précédente s'applique et la valeur g/d_i est celle d'un entier algébrique, c'est aussi un nombre rationnel et donc un élément de Z. Ce qui démontre que d_i divise l'ordre du groupe.

Groupe abélien

Article détaillé : Analyse harmonique sur un groupe abélien fini.

Si le groupe est abélien, il est aisé d'établir le groupe dual de G. Il est fini et isomorphe à G. L'algèbre du groupe complexe possède alors tous les outils de l'analyse harmonique. On définit une transformée de Fourier et un produit de convolution, et les théorèmes comme l'égalité de Parseval, le théorème de Plancherel ou la dualité de Pontryagin s'appliquent.

Il existe de nombreuses application à l'analyse harmonique sur un groupe abélien fini, on peut citer en arithmétique la constitution d'outils comme le symbole de Legendre, les sommes de Gauss utilisées pour la démonstration de la loi de réciprocité quadratique ou pour le calcul des périodes de Gauss et la recherche des racines du polynôme cyclotomique.

Notes et références

Articles sur les Représentations d'un groupe d'ordre fini

Liens externes

(fr) Cours de représentation des groupes finis par M. Broué de l'université de Paris VII
(fr) Représentation linéaire des groupes finis, une introduction par D. Ferrand de l'université de Renne
(en) Finite group representations for the pure mathematician par Peter Web

Références

Jean-Pierre Serre, Représentations linéaires des groupes finis [détail des éditions]
(en) Marshall Hall, The theory of groups [détail des éditions]
Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808) [détail des éditions]
N. Bourbaki Algèbre, Chapitre VIII Paris, Hermann 1958

Portail des mathématiques

Ce document provient de « Alg%C3%A8bre d%27un groupe fini ».

Catégorie : Théorie des représentations

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Algebre d'un groupe fini de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Algèbre D'un Groupe Fini — En mathématiques, l algèbre d un groupe fini s inscrit dans le cadre de la théorie des représentations d un groupe fini. Une algèbre d un groupe fini est la donnée d un groupe fini, d un espace vectoriel de dimension l ordre du groupe et d une… … Wikipédia en Français
Algèbre d'un groupe fini — Pour les articles homonymes, voir Algèbre (homonymie). En mathématiques, l algèbre d un groupe fini est un cas particulier d algèbre d un monoïde qui s inscrit dans le cadre de la théorie des représentations d un groupe fini. Une algèbre d un… … Wikipédia en Français
Representations d'un groupe fini — Représentations d un groupe fini En mathématiques, un groupe est une structure algébrique dont la définition est remarquablement simple. Elle consiste en un ensemble muni d une unique opération. Cette opération possède de bonnes propriétés, elle… … Wikipédia en Français
Représentations d'un groupe fini — En mathématiques, un groupe est une structure algébrique qui consiste en un ensemble muni d une unique opération. Cette opération possède de bonnes propriétés, elle est associative, il existe un élément neutre et tout élément admet un inverse. Un … Wikipédia en Français
Caractere d'un groupe fini — Caractère d un groupe fini En mathématiques, un caractère d un groupe fini est une notion associée à la théorie des groupes. Un caractère d un groupe fini G est un morphisme du groupe G dans C* le corps des nombres complexes non nuls. Ce concept… … Wikipédia en Français
Caractère D'un Groupe Fini — En mathématiques, un caractère d un groupe fini est une notion associée à la théorie des groupes. Un caractère d un groupe fini G est un morphisme du groupe G dans C* le corps des nombres complexes non nuls. Ce concept permet de définir le groupe … Wikipédia en Français
Theorie des representations d'un groupe fini — Théorie des représentations d un groupe fini Ferdinand Georg Frobenius, fondateur de la théorie de la représentation des groupes. En mathématiques et plus précisément en théorie des groupes, la théorie des représentations d un groupe fini est un… … Wikipédia en Français
Théorie des représentations d'un groupe fini — Ferdinand Georg Frobenius, fondateur de la théorie de la représentation des groupes. En mathématiques et plus précisément en théorie des groupes, la théorie des représentations d un groupe fini traite des représentations d un groupe G dans le cas … Wikipédia en Français
Fonction Centrale D'un Groupe Fini — En mathématiques et plus précisément en théorie des groupes une fonction centrale est une fonction définie sur un groupe et constante sur chaque classe de conjugaison. Les fonctions centrales possèdent un rôle particulier dans le cadre de la… … Wikipédia en Français
Fonction centrale d'un groupe fini — En mathématiques et plus précisément en théorie des groupes une fonction centrale est une fonction définie sur un groupe et constante sur chaque classe de conjugaison. Les fonctions centrales possèdent un rôle particulier dans le cadre de la… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Algebre d'un groupe fini

Algèbre d'un groupe fini

Sommaire

Introduction

Nature de la démarche

Applications

Définitions

Algèbre d'un groupe

G-module

Propriétés

Représentation régulière

Théorème d'Artin-Wedderburn

Centre de l'algèbre

Orthogonalité

Applications

Réciprocité de Frobenius

Entier algébrique

Groupe abélien

Notes et références

Liens externes

Références

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Algebre d'un groupe fini

Algèbre d'un groupe fini

Sommaire

Introduction

Nature de la démarche

Applications

Définitions

Algèbre d'un groupe

G-module

Propriétés

Représentation régulière

Théorème d'Artin-Wedderburn

Centre de l'algèbre

Orthogonalité

Applications

Réciprocité de Frobenius

Entier algébrique

Groupe abélien

Notes et références

Liens externes

Références

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link