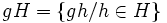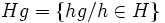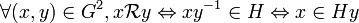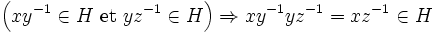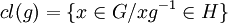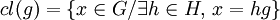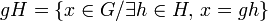Classe Suivant Un Sous-groupe

Classe suivant un sous-groupe

En théorie des groupes, les classes d'un groupe G selon un sous-groupe H sont les orbites de l'action de ce sous-groupe H sur G par translation à gauche ou à droite selon l'usage qui en est fait. Il est aussi possible de définir ces classes comme des classes pour une relation d'équivalence. L'ensemble de ces classes est usuellement noté H\G ou G/H. Ces ensembles sont naturellement munis d'une action transitive à droite ou à gauche de G. Ces ensembles servent de modèles pour les espaces homogènes.

L'utilisation des classes intervient notamment dans l'étude des groupes finis, à travers le théorème de Lagrange, les théorèmes de Sylow. Lorsque le sous-groupe est stable par conjugaison (on parle de sous-groupe normal), l'ensemble des classes G/H est naturellement muni d'une structure de groupes, appelée groupe quotient.

En pratique, hors de la théorie proprement dite des groupes, les classes selon les sous-groupes interviennent pour étudier les orbites d'une action de groupe, et définir notamment le type d'une orbite.

Définitions

Ce paragraphe donne uniquement les définitions ensemblistes des classes à gauche et à droite du sous-groupe $H$ de $G$ . La justification de cette définition et les propriétés qui y sont liées font l'objet des paragraphes suivants.

Soit $g \in G$ .

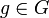On appelle classe à gauche suivant $H$ l'ensemble $g H$ défini par :

$gH=\{g h / h \in H \}$

On appelle classe à droite suivant $H$ l'ensemble $H g$ défini par :

$Hg=\{ h g / h \in H \}$

Relation d'équivalence

On définit une relation 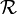$\mathcal{R}$ dans le groupe $G$ par :

$\forall (x,y)\in G^2, x\mathcal{R} y \Leftrightarrow xy^{-1} \in H \Leftrightarrow x \in Hy$

Cette relation 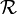$\mathcal{R}$ est alors une relation d'équivalence sur $G$ .

Démonstration que 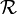$\mathcal{R}$ est bien une relation d'équivalence

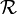$\mathcal{R}$ est réflexive.

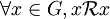$\forall x \in G, x\mathcal{R} x \,$ car :

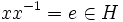
$x x^{-1}=e \in H \,$

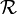$\mathcal{R}$ est symétrique.

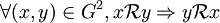$\forall (x,y) \in G^2, x\mathcal{R} y \Rightarrow y\mathcal{R} x \,$ car :

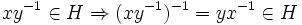
$xy^{-1} \in H \Rightarrow (xy^{-1})^{-1}=yx^{-1} \in H \,$

$R$ est transitive.

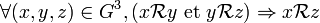$\forall (x,y,z) \in G^3, (x\mathcal{R} y \mbox{ et } y\mathcal{R} z) \Rightarrow x\mathcal{R} z \,$ car :

$\left( xy^{-1} \in H \mbox{ et } yz^{-1} \in H \right) \Rightarrow xy^{-1}yz^{-1}=xz^{-1} \in H \,$

La relation 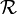$\mathcal{R}$ est réflexive, symétrique, et transitive, donc elle définit une relation d'équivalence sur le groupe $G$ .

Il est intéressant de noter que chacune des propriétés de la relation d'équivalence est directement reliée à une propriété de $H$ en tant que sous-groupe.

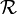$\mathcal{R}$ est réflexive car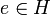 $e \in H$

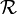$\mathcal{R}$ est transitive car

H

est stable pour la loi de composition.

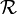$\mathcal{R}$ est symétrique car

H

est stable par inversion.

Classes d'équivalence

La relation 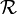$\mathcal{R}$ définie au paragraphe précédent est une relation d'équivalence donc elle donne une partition du groupe G en classes d'équivalence.

Soit 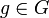$g \in G$ . Si on note $c l (g)$ la classe d'équivalence à laquelle appartient $g$ , alors :

$cl(g)=\{x \in G / xg^{-1} \in H\}$

c'est-à-dire :

$cl(g)=\{x \in G / \exists h \in H, \, x=hg \}$

Cet ensemble est généralement noté $H g$ et appelé classe à droite de $H$ .

On définit de la même façon les classes à gauche de H. Ce sont les ensembles, notés $g H$ , définis par

$gH=\{x \in G /\exists h \in H, \, x=gh\}$

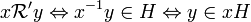Ces ensembles sont les classes d'équivalence de la relation d'équivalence suivante : $x\mathcal{R}'y \Leftrightarrow x^{-1}y \in H\Leftrightarrow y \in xH$ .

Quelques propriétés

On a gH = H si et seulement si g est un élément de H.

Deux quelconques classes à gauche, ou classes à droite, sont égales ou disjointes.

Si H est un sous-groupe fini, alors toutes ses classes à droite et à gauche ont même nombre d'éléments.

De plus, si G est un groupe fini, alors le nombre de classes à gauche (ou à droite) de H est égal au quotient de l'ordre de G par celui de H.

Le sous-groupe H est dit distingué ou normal ou invariant si et seulement si pour tout g dans G, la classe à gauche gH est égale à la classe à droite Hg.

Références

Ouvrages

Liens internes

Notes et références

Portail des mathématiques

Ce document provient de « Classe suivant un sous-groupe ».

Catégorie : Théorie des groupes

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Classe Suivant Un Sous-groupe de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Classe suivant un sous-groupe — En théorie des groupes, les classes à gauche d un groupe G suivant un sous groupe H sont les parties de G de la forme gH avec g élément de G, où gH désigne l ensemble des éléments gh quand h parcourt H. Elles constituent les classes d une… … Wikipédia en Français
Groupe (mathématique) — Groupe (mathématiques) Pour les articles homonymes, voir Groupe. Cet article concerne une introduction au concept de groupe. Pour un approfondissement, voir théorie des groupes … Wikipédia en Français
Groupe (mathématiques) — Pour les articles homonymes, voir Groupe. Les manipulations possibles du cube de Rubik forment un groupe. En mathématiques, un groupe est un ensemble … Wikipédia en Français
Groupe Libre — Le groupe libre sur un ensemble S est le groupe F contenant S et caractérisé par la propriété universelle suivante : pour tout groupe G et toute application ensembliste f de S dans G, il existe un unique morphisme de groupe de F dans G… … Wikipédia en Français
Structure de groupe — Groupe (mathématiques) Pour les articles homonymes, voir Groupe. Cet article concerne une introduction au concept de groupe. Pour un approfondissement, voir théorie des groupes … Wikipédia en Français
Théorie de Groupe — Groupe (mathématiques) Pour les articles homonymes, voir Groupe. Cet article concerne une introduction au concept de groupe. Pour un approfondissement, voir théorie des groupes … Wikipédia en Français
Groupe libre — En théorie des groupes, le groupe libre sur un ensemble S est le groupe F contenant S et caractérisé par la propriété universelle suivante : pour tout groupe G et toute application f : S → G, il existe un unique morphisme de groupes de… … Wikipédia en Français
Groupe Alterné — En mathématiques, et plus précisément en théorie des groupes, le groupe alterné de degré n, souvent noté An, est un sous groupe distingué du groupe symétrique des permutations d un ensemble fini de cardinal n. Ce sous groupe est composé des… … Wikipédia en Français
Groupe alterne — Groupe alterné En mathématiques, et plus précisément en théorie des groupes, le groupe alterné de degré n, souvent noté An, est un sous groupe distingué du groupe symétrique des permutations d un ensemble fini de cardinal n. Ce sous groupe est… … Wikipédia en Français
groupe — [ grup ] n. m. • 1668; it. gruppo « nœud, assemblage », d o. germ. °kruppa « masse arrondie »; cf. croupe 1 ♦ Réunion de plusieurs personnages, formant une unité organique dans une œuvre d art (peinture, sculpture). Le groupe des trois Grâces. 2… … Encyclopédie Universelle

Dictionnaires et Encyclopédies sur 'Academic'

Classe Suivant Un Sous-groupe