Produit tensoriel et representations de groupes finis

Produit tensoriel et représentations de groupes finis

En mathématiques et plus précisément dans le cadre des représentations d'un groupe fini, le produit tensoriel est une technique permettant de construire une représentation à partir de deux autres.

Si un groupe fini G est produit direct de deux groupes, alors toute représentation irréductible de G est isomorphe à un produit tensoriel des deux groupes.

Sommaire

1 Contexte
2 Définitions
3 Propriétés
- 3.1 produit tensoriel et produit direct
4 Caractère
- 4.1 Cas des représentations irréductibles
- 4.2 Cas d'une représentation d'un groupe produit
5 Notes et références
- 5.1 Liens externes
- 5.2 Références

Contexte

Produit tensoriel

Article détaillé : Produit tensoriel.

Produit tensoriel de deux espaces vectoriels

Soient V et W deux espaces vectoriels sur un corps commutatif K de dimensions finies respectives n et m. Le produit tensoriel de V et W, noté V $\otimes$ W correspond à l'espace vectoriel des formes de VxW dans K linéaire en V et en W. C’est-à-dire :

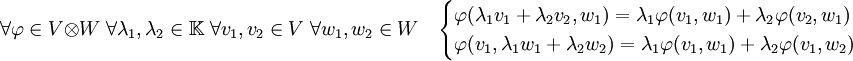
$\forall \varphi \in V\otimes W\; \forall \lambda_1,\lambda_2 \in \mathbb K \; \forall v_1,v_2 \in V \;\forall w_1,w_2 \in W \quad \begin{cases} \varphi(\lambda_1 v_1+\lambda_2 v_2,w_1)=\lambda_1 \varphi(v_1,w_1)+\lambda_2 \varphi(v_2,w_1) \\ \varphi(v_1,\lambda_1 w_1+\lambda_2 w_2)=\lambda_1 \varphi(v_1,w_1)+\lambda_2 \varphi(v_1,w_2) \end{cases}$

Soit (a_i) (resp. (b_j)) une base de V (resp. W), il est alors possible d'identifier V (resp. W) à son espace dual. En effet, soit u (resp. v) un vecteur de V (resp. W) de coordonnées (α_i) (resp. (β_j)) dans la base précédente, alors a_i (resp. b_j) est identifié à la forme linéaire suivante :

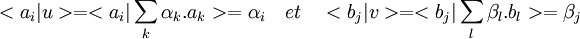
$<a_i|u>=<a_i|\sum_k \alpha_k.a_k>=\alpha_i \quad et \quad <b_j|v>=<b_j|\sum_l \beta_l.b_l>=\beta_j$

Cette identification établit une application canonique $\otimes$ de VxW vers V $\otimes$ W défini, avec les notations précédentes par :

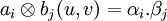
$a_i\otimes b_j (u,v) = \alpha_i.\beta_j$

La famille (a_i $\otimes$ b_j) est alors la base canonique de V $\otimes$ W. En utilisant les trois bases, on obtient l'égalité :

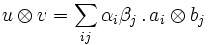
$u\otimes v = \sum_{ij} \alpha_i\beta_j\,.\, a_i\otimes b_j$

Passage aux endomorphismes

L'application précédente $\otimes$ désigne aussi une application de L(V)xL(W) dans L (V $\otimes$ W). Ici L(E) désigne l'espace vectoriel des endomorphismes de E. soit φ (resp. ψ) un endomorphisme L(V) (resp. L(W)), alors, avec les notations précédentes, on obtient :

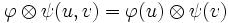
$\varphi\otimes\psi (u,v) =\varphi(u)\otimes\psi(v)$

Si (α_ik) (resp (β_jl)) désigne la matrice de φ (resp. ψ), alors la matrice M de φ $\otimes$ ψ dans la base a_i $\otimes$ b_j est la suivante :

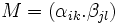
$M=(\alpha_{ik}.\beta_{jl})\;$

Déterminons la trace de φ $\otimes$ ψ. Calculons l'image de a_i $\otimes$ b_j par l'endomorphisme :

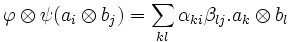
$\varphi\otimes\psi(a_i\otimes b_j) =\sum_{kl}\alpha_{ki}\beta_{lj}.a_k\otimes b_l$

Le terme diagonal correspondant au vecteur a_i $\otimes$ b_j de la base est donc α_ii.β_jj. La somme de tous les termes diagonaux de la matrice M est donc :

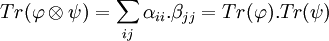
$Tr (\varphi\otimes\psi) = \sum_{ij} \alpha_{ii}.\beta_{jj}=Tr(\varphi).Tr(\psi)$

Ici, Tr désigne l'application qui à un endomorphisme associe sa trace. La trace d'un produit tensoriel de deux endormorphismes est donc égale au produit des traces des endomorphismes.

Cas où W est égal à V

Si W est égal à V, V $\otimes$ V est égal à l'espace de dimension n² des forme bilinéaires de V. Cet espace possède deux supplémentaires S l'espace des formes bilinéaires symétriques de dimension n.(n + 1)/2 et A l'espace vectoriel des formes bilinéaires alternées de dimension n.(n - 1)/2.

Le projecteur sur S parallèlement à A associe à a_i $\otimes$ a_j la forme bilinéaire symétrique : 1/2(a_i $\otimes$ a_j + a_j $\otimes$ a_i).

Produit direct de deux groupes

Article détaillé : Produit direct (groupes).

L'un des objectifs de la représentation des groupes finis est la classification. La théorie classique utilise les techniques de l'extension pour générer des classes de groupes. Le produit direct est une des deux méthodes d'extension, elle correspond à la plus simple.

L'ensemble G, produit cartésien des deux groupes G₁ et G₂ et muni de la loi suivante *, est appelé produit direct des groupes G₁ et G₂ :

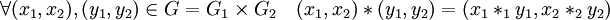
$\forall (x_1,x_2),(y_1, y_2) \in G=G_1\times G_2 \quad (x_1,x_2)*(y_1,y_2) = (x_1*_1y_1,x_2*_2y_2) \;$

Le produit direct permet une classification simple des groupes abéliens finis :

Si l'ordre d'un groupe abélien fini G est différent de un, il existe une et une unique décomposition de G en produit de cycles d'ordre une puissance différente de zéro d'un nombre premier.

Représentations d'un groupe fini

Article détaillé : Représentations d'un groupe fini.

Rappelons la définition d'une représentation et fixons les notations pour le reste de l'article. G désigne ici un groupe fini d'ordre g. Son élément neutre est noté 1, et si s et t sont deux éléments de G la loi de composition interne du groupe sur s et t est noté st. V désigne un espace vectoriel sur un corps noté K de caractéristique première avec g ou nulle.

Une représentation du groupe G est la donnée d'un espace vectoriel V de dimension finie notée n et d'un morphisme de groupe ρ de G vers le groupe linéaire GL(V). Une représentation est notée (V, ρ) ou parfois et abusivement V.

C'est-à-dire que l'application ρ est à valeur dans l'espace des applications linéaires bijectives et préserve la loi du groupe, ce qui est équivalent à :

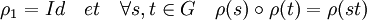
$\rho_1=Id \quad et \quad \forall s, t \in G \quad \rho(s)\circ \rho(t) = \rho(st)$

Définitions

Produit tensoriel de deux représentations d'un même groupe

Le produit tensoriel est compatible avec les représentations, ce qui signifie que l'on peut définir le produit tensoriel de deux représentations. Soit (V₁, ρ¹) et (V₂, ρ²) deux représentations d'un groupe de degré respectif n₁ et n₂, soit (e¹_i) une base de V₁, (e²_j) une base de V₂, on considère la base (e¹_i $\otimes$ e²_j) de V₁ $\otimes$ V₂.

Le produit tensoriel permet d'associer aux deux représentations une représentation ρ sur le produit tensoriel des deux espaces et définie par :

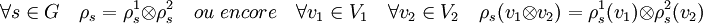
$\forall s \in G \quad \rho_s=\rho^1_s\otimes\rho^2_s \quad ou \; encore\quad \forall v_1 \in V_1 \quad \forall v_2 \in V_2\quad \rho_s (v_1\otimes v_2)=\rho^1_s (v_1)\otimes\rho^2_s (v_2)$

Montrons que (V₁ $\otimes$ V₂, ρ) est une représentation. Il suffit pour cela de montrer que :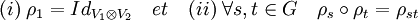

$(i)\;\rho_{1}=Id_{V_1\otimes V_2} \quad et \quad (ii)\; \forall s,t \in G \quad \rho_s\circ\rho_t=\rho_{st}$

Il suffit de montrer les égalités (i) et (ii) sur un élément quelconque de la base (e¹_i $\otimes$ e²_j)

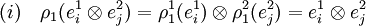
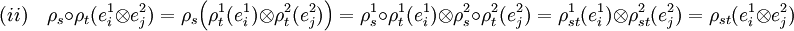
$(i)\quad \rho_{1}(e_i^1\otimes e_j^2)=\rho^1_1 (e_i^1)\otimes\rho^2_1 (e_j^2)=e_i^1\otimes e_j^2$ $(ii)\quad \rho_{s}\circ\rho_{t} (e_i^1\otimes e_j^2)=\rho_{s}\Big(\rho^1_t (e_i^1)\otimes\rho^2_t (e_j^2)\Big)= \rho^1_s\circ\rho^1_t (e_i^1)\otimes\rho^2_s\circ\rho^2_t (e_j^2)=\rho^1_{st} (e_i^1)\otimes\rho^2_{st} (e_j^2)=\rho_{st} (e_i^1\otimes e_j^2)$

Carré symétrique et alterné

Dans le cas général le produit tensoriel de deux représentations irréductibles n'est pas irréductible.

Il existe un cas particulier important, celui où V₁ est égal à V₂, notons alors V ces deux espaces et n leur dimension, et supposons que les deux représentations associées soit identiques. Le produit tensoriel possède deux sous-espaces supplémentaires Sym (V) et Alt(V) correspondant aux formes bilinéaires symétriques et alternées. Ces deux sous-espaces sont stables pour la représentation tensoriel. Démontrons le pour les formes bilinéaires symétriques : soit s une forme bilinéaire symétrique. Alors, l'expression de s dans la base (e_i $\otimes$ e_j) est de la forme suivante :

$\exists s_{ij} \in K \; avec \quad i,j \in [1,n] \; et \; j \ge i\quad s = \sum_{i\le j} s_{ij}(e_i\otimes e_j + e_j\otimes e_i)$

Si u est élément de G alors :

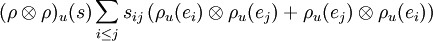
$(\rho\otimes\rho)_u(s)\sum_{i\le j} s_{ij}\left(\rho_u (e_i)\otimes \rho_u (e_j) + \rho_u (e_j)\otimes \rho_u (e_i)\right)$

La dernière expression est bien celle d'une forme bilinéaire symétrique, ce qui montre la stabilité de Sym (V). Un raisonnement analogue montre celle de Alt(V).

Le sous-espace Sym (V) (resp. Alt(V)) est un sous-espace stable de la représentation tensorielle (V $\otimes$ V, ρ $\otimes$ ρ) appelé carré symétrique (resp. carré alterné).

Produit tensoriel de deux groupes

Soit (V₁, ρ¹) une représentation d'un groupe G₁ et (V₂, ρ²) une représentation d'un groupe G₂. Considérons l'application ρ¹ $\otimes$ ρ², c'est une application de G₁ x G₂ dans L(V₁ $\otimes$ V₂). Cette application est un morphisme. En effet, en utilisant les notations précédentes, on obtient :

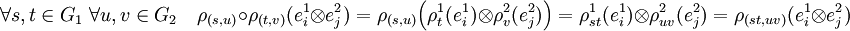
$\forall s,t \in G_1 \; \forall u,v \in G_2\quad \rho_{(s,u)}\circ\rho_{(t,v)}(e_i^1\otimes e_j^2)= \rho_{(s,u)}\Big(\rho_t^1(e_i^1)\otimes\rho_v^2(e_j^2)\Big)=\rho_{st}^1(e_i^1)\otimes\rho_{uv}^2(e_j^2)=\rho_{(st,uv)}(e_i^1\otimes e_j^2)$

Le produit tensoriel de deux représentations de deux groupes correspond donc à une représentation du groupe produit dans le produit tensoriel des deux espaces. Remarque, la notation est ambiguë. En effet, dans le cas où G₁ et G₂ représente le même groupe G, (V₁ $\otimes$ V₂, ρ) désigne à la fois une représentation de G et de GxG. La première représentant la restriction de la deuxième à la diagonale, le contexte nécessite une précision.

Propriétés

produit tensoriel et produit direct

Soit G un groupe contenant deux sous-groupes G₁ et G₂ tel que G soit isomorphe au produit direct de G₁ et de G₂. Il existe deux manières d'obtenir des représentations de G à partir de celles de G₁ et de celles G₂, soit à partir d'une somme directe d'une représentation de G₁ et d'une représentation de G₂ soit à l'aide d'un produit tensoriel.

La somme directe n'est guère efficace, en effet, seules les représentations irréductibles sont véritablement intéressantes, elles forment en effet la base de toutes les autres (cf théorème de Maschke). Or une somme directe ne fournit jamais une représentation irréductible, en effet, V₁ x {0} et {0} x V₂ sont toujours des sous-espaces invariants.

Le produit tensoriel fournit en revanche les représentations irréductibles de G. Toute représentation irréductible est le produit tensoriel de représentations irréductibles de G₁ et de G₂ et le produit tensoriel de deux représentations irréductibles de G₁ et de G₂ est une représentation irréductible de G.

Caractère

Cas des représentations irréductibles

On suppose ici que les caractères irréductibles forment une base orthonormale, par exemple parce que le corps K est celui des nombres complexes.

Le produit tensoriel (V, ρ) de deux représentations irréductibles (V₁, ρ¹) et (V₂, ρ²) de deux groupes G₁ et G₂ est irréductible.

Le caractère de ρ (resp. ρ¹) (resp. ρ²) est noté χ (resp. χ₁) (resp. χ₂). Pour démontrer que ρ est irréductible, il suffit de vérifier que <χ|χ> est égal à un. La trace d'un produit tensoriel de deux endormorphismes est égale au produit des traces des deux endomorphismes. Dans le cas des représentations, on obtient la formule :

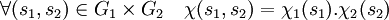
$\forall (s_1,s_2) \in G_1\times G_2 \quad \chi (s_1,s_2)=\chi_1(s_1).\chi_2(s_2)$

De plus, <χ₁|χ₁> et <χ₂|χ₂> sont égaux à un car les deux représentations associées sont irréductibles, on en déduit si g_i désigne l'ordre de G_i :

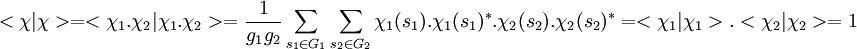
$<\chi|\chi>=<\chi_1.\chi_2|\chi_1.\chi_2>=\frac{1}{g_1g_2}\sum_{s_1\in G_1} \sum_{s_2 \in G_2}\chi_1(s_1).\chi_1(s_1)^*.\chi_2(s_2).\chi_2(s_2)^*=<\chi_1|\chi_1>.<\chi_2|\chi_2>=1 \;$

Ce qui termine la démonstration.

Cas d'une représentation d'un groupe produit

On suppose ici que G contient deux sous-groupes G₁ et G₂ tel que G soit isomorphe au produit direct G₁ x G₂. Il existe une bijection entre le produit cartésien des représentations irréductibles de G₁ et G₂ et celles de G données par le produit tensoriel des représentations. Le paragraphe précédent montre que le produit tensoriel des représentations irréductibles est bien à valeur dans les représentations irréductibles de G.

Montrons que l'application est surjective. Soit (V, ρ) une représentation irréductible de G.

Il existe une représentation irréductible (V₁, ρ¹) de G₁ et une (V₂, ρ²) de G₂ tel que (V, ρ) est isomorphe au produit tensoriel des deux représentations précédentes.

Pour cela, il suffit de montrer que l'ensemble des produits tensoriels de représentations irréductibles de G₁ et G₂ forment une base orthonormale des fonctions centrales de G. Soit f est une fonction centrale de G orthogonale à tout produit tensoriel de caractères irréductibles. Montrer que f est la fonction nulle démontre la proposition. On a, avec les notations précédentes :

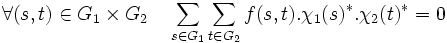
$\forall (s,t) \in G_1\times G_2 \quad \sum_{s\in G_1} \sum_{t \in G_2} f(s,t).\chi_1(s)^*.\chi_2(t)^*=0$

Notons f_s la fonction de G₂ dans K qui à t associe f(s,t)χ₁(s). f_s est une fonction centrale orthogonale à tout caractère irréductible de G₂, f_s est donc la fonction nulle. En conséquence :

$\forall (s,t) \in G_1\times G_2 \quad f(s,t).\chi_1(s)^*=0$

Soit t un élément quelconque de G₂, la fonction de G₁ dans K, qui à s associe f(s,t) est orthogonale à tout caractère irréductible de G₁, c'est donc aussi la fonction nulle. La proposition est alors démontrée.

Pour montrer que l'application des couples de représentations irréductibles de G₁ x G₂ dans celle de G donnée par le produit tensoriel est injectif, deux remarques suffisent. Le nombre de représentations irréductibles d'un groupe fini est égal au nombre de classes de conjugaison du groupe. Comme le nombre de classes de conjugaison de G est égal au produit des nombres de classes de conjugaison de G₁ et G₂, le nombre de caractères irréductibles de G est égal au produit du nombre de caractères irréductibles de G₁ et G₂. L'égalité des cardinaux de l'ensemble de départ et d'arrivé ainsi que la surjectivité démontre l'injectivité.

Notes et références

Liens externes

(fr) Cours de représentation des groupes finis par M. Broué de l'université de Paris VII
(fr) Représentation linéaire des groupes finis, une introduction par D. Ferrand de l'université de Renne

Références

Jean-Pierre Serre, Représentations linéaires des groupes finis [détail des éditions]
(en) Marshall Hall, The theory of groups [détail des éditions]
Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808) [détail des éditions]
N. Bourbaki Algèbre, Chapitre VIII Paris, Hermann 1958

Articles sur les Représentations d'un groupe d'ordre fini

Ce document provient de « Produit tensoriel et repr%C3%A9sentations de groupes finis ».

Catégorie : Théorie des représentations

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Produit tensoriel et representations de groupes finis de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Produit tensoriel et représentations de groupes finis — En mathématiques et plus précisément dans le cadre de la théorie des représentations d un groupe fini, le produit tensoriel est une technique permettant de construire une représentation d un groupe fini à partir de deux autres. Une représentation … Wikipédia en Français
Représentations des groupes finis — Représentations d un groupe fini En mathématiques, un groupe est une structure algébrique dont la définition est remarquablement simple. Elle consiste en un ensemble muni d une unique opération. Cette opération possède de bonnes propriétés, elle… … Wikipédia en Français
Representations du groupe des quaternions — Représentations du groupe des quaternions En mathématiques les représentations du groupe des quaternions sont un exemple d application de la théorie des représentations d un groupe fini. Il illustre le théorème d Artin Wedderburn et met en… … Wikipédia en Français
Représentation des groupes finis — Représentations d un groupe fini En mathématiques, un groupe est une structure algébrique dont la définition est remarquablement simple. Elle consiste en un ensemble muni d une unique opération. Cette opération possède de bonnes propriétés, elle… … Wikipédia en Français
Représentations du groupe des quaternions — En mathématiques les représentations du groupe des quaternions sont un exemple d application de la théorie des représentations d un groupe fini. Il illustre le théorème d Artin Wedderburn et met en évidence un corps gauche (c est à dire non… … Wikipédia en Français
Theorie des representations d'un groupe fini — Théorie des représentations d un groupe fini Ferdinand Georg Frobenius, fondateur de la théorie de la représentation des groupes. En mathématiques et plus précisément en théorie des groupes, la théorie des représentations d un groupe fini est un… … Wikipédia en Français
Théorie des représentations d'un groupe fini — Ferdinand Georg Frobenius, fondateur de la théorie de la représentation des groupes. En mathématiques et plus précisément en théorie des groupes, la théorie des représentations d un groupe fini traite des représentations d un groupe G dans le cas … Wikipédia en Français
Representations d'un groupe fini — Représentations d un groupe fini En mathématiques, un groupe est une structure algébrique dont la définition est remarquablement simple. Elle consiste en un ensemble muni d une unique opération. Cette opération possède de bonnes propriétés, elle… … Wikipédia en Français
Representations du groupe symetrique d'indice quatre — Représentations du groupe symétrique d indice quatre Graphe de Cayley du groupe symétrique d indice quatre en tant que groupe de rotations d un dé standard. En mathématiques les représentations du groupe symétrique d indice quatre noté S4 sont un … Wikipédia en Français
Représentations du groupe symétrique d'ordre quatre — Représentations du groupe symétrique d indice quatre Graphe de Cayley du groupe symétrique d indice quatre en tant que groupe de rotations d un dé standard. En mathématiques les représentations du groupe symétrique d indice quatre noté S4 sont un … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Produit tensoriel et representations de groupes finis

Produit tensoriel et représentations de groupes finis

Sommaire

Contexte

Produit tensoriel

Produit tensoriel de deux espaces vectoriels

Passage aux endomorphismes

Cas où W est égal à V

Produit direct de deux groupes

Représentations d'un groupe fini

Définitions

Produit tensoriel de deux représentations d'un même groupe

Carré symétrique et alterné

Produit tensoriel de deux groupes

Propriétés

produit tensoriel et produit direct

Caractère

Cas des représentations irréductibles

Cas d'une représentation d'un groupe produit

Notes et références

Liens externes

Références

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Produit tensoriel et representations de groupes finis

Produit tensoriel et représentations de groupes finis

Sommaire

Contexte

Produit tensoriel

Produit tensoriel de deux espaces vectoriels

Passage aux endomorphismes

Cas où W est égal à V

Produit direct de deux groupes

Représentations d'un groupe fini

Définitions

Produit tensoriel de deux représentations d'un même groupe

Carré symétrique et alterné

Produit tensoriel de deux groupes

Propriétés

produit tensoriel et produit direct

Caractère

Cas des représentations irréductibles

Cas d'une représentation d'un groupe produit

Notes et références

Liens externes

Références

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link