- Caractere d'un groupe topologique compact
-
Caractère d'un groupe topologique compact
Dans l'étude des représentations d'un groupe topologique compact, les caractères sont des fonctions centrales (id est constantes sur les classes de conjugaison) associées aux représentations et permettant de caractériser les classes d'équivalence des représentations irréductibles de dimension finie. En particulier, on démontre qu'il existe un nombre au plus dénombrable de classes d'équivalence de représentations irréductibles d'un groupe compact. Par ailleurs, la décomposition d'une représentation en somme orthogonale de représentations irréductibles se comprend en termes de décomposition en séries du caractère associé dans l'algèbre hilbertienne associée au groupe.
Sommaire
Définition
G désigne un groupe topologique compact. Une représentation complexe de G de dimension finie est une application continue
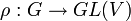. On appelle caractère associé à ρ l'application χρ définie par :![\forall s\in G, \, \chi_{\rho}(s)=Tr\left[\rho(s)\right]](/pictures/frwiki/50/2ca15573d76523fc85e37086a8900ba7.png)
.où Tr désigne la trace. On parle simplement de caractère ou de caractère irréductible pour désigner le caractère associé à une représentation ou une représentation irréductible.
Deux représentations
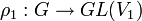et 
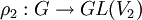sont équivalentes s'il existe un isomorphisme linéaire 
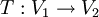tel que pour tout 
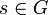on a : 
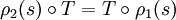. De manière évidente, les caractères associés à des représentations équivalentes sont égaux.Pour un groupe compact, toute représentation est équivalente à une représentation unitaire. Certains auteurs ne parlent donc dans ce cadre que de représentations unitaires.
Sommes et produits tensoriels
Article détaillé : Construction de représentations.Le caractère associé à une représentation unitaire est égal au conjugué du caractère associé à sa représentation duale :
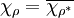.Le caractère associé à la somme directe de deux représentations unitaires est égal à la somme des caractères qui leur sont associées :
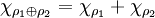.Le caractère associé au produit tensoriel de deux représentations unitaires est égal au produit des caractères qui leur sont associées :
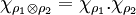.Propriétés élémentaires
- Un caractère est une fonction continue de carré intégrable contre la mesure de Haar.
La composition d'applications continues est continue. Le caractère associé à une représentation de dimension finie ρ est la composée de la trace et de ρ, donc est continu. De plus, pour tout opérateur A sur un espace vectoriel complexe de dimension finie n, on dispose de l'inégalité
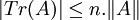. En supposant la représentation unitaire, le caractère est une fonction continue bornée, a fortiori de carré intégrable, car λ est une mesure finie.- Les caractères sont des fonctions centrales : ils sont constants sur les classes de conjugaison de G.
En effet, pour tous s et t dans G, on a :
![\chi_{\rho}(sts^{-1})=Tr\left[\rho(sts^{-1})\right]=Tr\left[\rho(s)\rho(t)\rho(s)^{-1})\right]=Tr\left[\rho(t)\right]=\chi_{\rho}(t)](/pictures/frwiki/54/6bb2e0c11932bc8bed5b2d3c73517b18.png)
.- Pour deux représentations irréductibles non équivalentes ρ et σ, les caractères associés sont orthogonaux au sens où
.
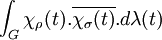Soient
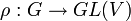et 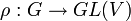deux représentations de G de dimensions finies respectives m et n et non équivalentes. Pour toute application linéaire 
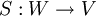, on pose :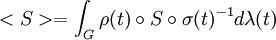
On vérifie sans difficulté :
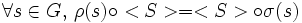.Comme ρ et σ ne sont pas équivalentes, < S > n'est pas un isomorphisme linéaire. Par le lemme de Schur, < S > est nul. Quitte à choisir des bases arbitraires, on peut supposer
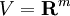et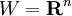 
et on note ![\rho(t)=\left[\rho_{ij}(t)\right]](/pictures/frwiki/97/a8aa12d0f95a7d1404e0004345012525.png)
et ![\sigma(t)^{-1}=\left[\sigma_{ij}(t)\right]](/pictures/frwiki/54/651f8884f55d8390ffddbb08bb531302.png)
. La nullité de < S > s'écrit :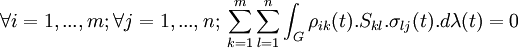
.D'où :
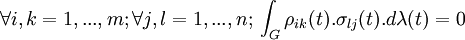.En particulier, un calcul donne :
![0=\sum_{i=1}^m\sum_{j=1}^n \int_G\rho_{ii}(t).\sigma_{jj}(t).d\lambda(t)=\int_G\left[\sum_{i=1}^m\rho_{ii}(t)\right].\left[\sum_{j=1}^n\sigma_{jj}(t)\right].d\lambda(t)=\int_G\chi_{\rho}(t).\overline{\chi_{\sigma}(t)}.d\lambda(t)](/pictures/frwiki/99/ce9d7c28a597583fc96e6e339a743c9c.png)
.Algèbre hilbertienne de G
Article détaillé : Algèbre hilbertienne d'un groupe topologique compact.Si G est un groupe compact, de mesure de Haar λ, l'espace de Banach L2(G) peut être muni du produit de convolution défini par :
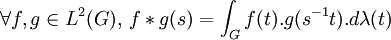
L2(G) est une algèbre de Banach. Son centre est le sous-espace fermé des fonctions centrales mesurables sur G de carré mesurable.
Les caractères forment une base hilbertienne du centre de l'algèbre L2(G).
Portail des mathématiques
Catégorie : Théorie des représentations des groupes topologiques
Wikimedia Foundation. 2010.
