Extension Séparable

Extension Séparable

Extension séparable

Une extension algébrique L d'un corps K est dite séparable si et seulement si le polynôme minimal de tout élément de L n'admet que des racines simples.

Ce critère est une hypothèse nécessaire pour établir un théorème important de la théorie de Galois: Le théorème de l'élément primitif. La séparabilité est aussi utilisée dans la définition d'une extension de Galois.

Les corps dont toutes les extensions algébriques sont séparables sont nombreux. On y trouve par exemple les corps de caractéristique nulle, ce qui recouvre les nombres rationnels, les nombres réels et les nombres complexes.

Sommaire

Motivation

Le groupe des automorphismes de corps est un puissant outil d'analyse d'une extension algébrique. Il est particulièrement efficace si le nombre de racines du polynôme minimal est toujours égal à son degré. Cette propriété est toujours vérifiée si le corps initial est de caractéristique nulle ou si le corps est fini. On parle alors du Groupe de Galois. En revanche, cette propriété n'est pas vraie sur tous les corps, la théorie de Galois qui est l'étude des extensions algébriques demande pour la démonstration de l'essentiel des théorèmes la séparabilité.

La première conséquence de la séparabilité est le théorème de l'élément primitif. Si une extension finie L sur un corps K est séparable alors il existe un élément l de L de polynôme minimal P(X) sur K tel que L soit le plus petit corps de rupture de P(X). Cela signifie que L est égal à K(l) ou encore que L est une extension simple.

Dans le cas ou l'extension est finie et séparable, alors il existe autant d'automorphismes que la dimension de l'extension. Si ses automorphismes laissent stable l'extension, on parle alors d'Extension de Galois. C'est le contexte initial et le la théorie de Galois. Il existe alors une bijection entre les sous-corps de l'extension et les sous-groupes du groupe de Galois. L'étude de ces sous-groupes permet par exemple de déterminer une condition nécessaire et suffisante pour la résolubilité par radicaux d'une équation polynomiale.

Définitions et premiers exemples

Dans la suite de l'article, K désigne un corps, L une extension algébrique, P(X) un polynôme formel à coefficients dans K et scindé sur L et l un élément de L. Ω désigne la clôture algébrique de K, dans cet article, toute extension est identifiée à un sous-corps de Ω. Cette identification est licite, d'après le paragraphe sur la clôture algébrique.

  • P(X) est séparable dans L si et seulement s'il possède autant de racines distinctes que son degré. Le polynôme est donc scindé sans racine multiple.
  • l est séparable dans K si et seulement si son polynôme minimal est séparable.
  • L est séparable dans K si et seulement si tous ses éléments le sont.
  • K est un corps parfait si et seulement si toutes ses extensions algébriques sont séparables.

Le polynôme X3-2 sur le corps des nombres rationnels est séparable. En effet, il possède trois racines, une réelle : la racine cubique de deux et deux complexes conjuguées entre elles. les trois racines sont distinctes. De manière générale sur les nombres rationnels, tout polynôme irréductible est séparable.

Cependant, tous les polynômes irréductibles ne sont pas séparables. Considérons Fp(X) le corps des fractions rationnelles sur le corps fini de cardinal p, où p est premier, et Ω sa clôture algébrique. Si K est choisi comme étant égal à l'ensemble des fractions de Fp(Xp), alors K contient un polynôme non séparable. Considérons le polynôme P(X) de K[Y] égal à Yp-Xp. Ce polynôme possède une unique racine X qui est donc un élément algébrique de degré p. De plus ce polynôme est irréductible. On en déduit que Fp(X) est le corps de décomposition du polynôme P(X). Comme X est sa seule racine, P(X) n'est pas séparable.

Critères de séparabilité

Cas des polynômes

L'analyse de la séparabilité d'une extension revient à l'analyse des propriétés des polynômes sur K. En effet, pour qu'une extension soit séparable il faut et il suffit que ses éléments le soit, ce qui signifie que leurs polynômes minimaux le soient aussi. Il apparaît alors nécessaire d'établir des critères de séparabilité d'un polynôme. Il en existe un particulièrement simple.

  • Un polynôme est séparable si et seulement si lui et sa dérivée formelle sont premiers entre eux.

Dans le cas d'un polynôme irréductible, car particulièrement intéressant dans le cadre de la théorie de Galois, cette proposition implique le corollaire suivant:

  • Un polynôme irréductible est séparable si et seulement si sa dérivé formelle n'est pas nulle.

Ce corollaire permet de résoudre simplement le cas des corps de caractéristique nulle.En particulier, les trois corps les plus usuels, les nombres rationnels, les nombres réels et les nombres complexes sont des corps parfaits. Il existe néanmoins un critère de séparabilité d'un polynôme irréductible.

  • Supposons K de caractéristique p et P(X) un polynôme irréductible. Il est séparable si et seulement s'il n'existe pas de polynôme Q[X] dans K[X] tel que l'on ait l'égalité P(X)=Q(Xp).


Démonstrations
  • Un polynôme P(X) élément de K[X] est séparable si et seulement si lui et sa dérivée formelle sont premiers entre eux.

Dire de P(X) n'est pas séparable revient à dire que ce polynôme s'écrit dans Ω[X] de la manière suivante (X-a)nQ[X], ou a est un élément de Ω et n un entier supérieur ou égal à deux. Alors la dérivée formelle de P(X) vérifie l'égalité suivante:

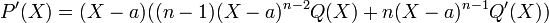
P'(X)=(X-a)((n-1)(X-a)^{n-2}Q(X)+n(X-a)^{n-1}Q'(X))\;

P(X) et P'(X) sont deux polynômes de K[X] qui ne sont pas premiers entre eux dans Ω[X], ils ne sont donc pas premiers entre eux dans K[X]. Et la proposition est démontrée.

  • Un polynôme irréductible est séparable si et seulement si sa dérivée formelle n'est pas nulle.

C'est un corollaire direct de la proposition précédente. Le seul polynôme de degré strictement inférieur à P(X) annulant a, une racine dans Ω de P(X) est le polynôme nul.

  • Supposons K de caractéristique p et P(X) un polynôme irréductible. Il est séparable si et seulement s'il n'existe pas de polynôme Q(X) dans K[X] tel que l'on ait l'égalité P(X)=Q(Xp).

Si le polynôme Q(X) existe avec la propriété de l'énoncée, alors la dérivée de P(X) vérifie l'égalité suivante:

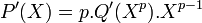
P'(X)=p.Q'(X^p).X^{p-1}\;

Comme le K est de caractéristique p, le polynôme dérivé est nul et la proposition précédente permet de conclure. Réciproquement si un tel polynôme n'existe pas, notons alors ai les coefficients du polynôme P(X). Alors la dérivée vérifie l'égalité suivante:

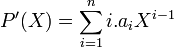
P'(X)=\sum_{i=1}^n i.a_i X^{i-1}\;

Comme P(X) n'est pas un polynôme en Xp il existe un coefficient ai qui n'est pas multiple de p avec i non plus car p est premier puisque K est un corps. Ce qui montre que la dérivée formelle de P(X) n'est pas nulle.

Cas des extensions et des corps

Article détaillé : Corps parfait.

Ce paragraphe précédent permet de résoudre simplement le cas des corps de caractéristique nulle.En particulier, les trois corps les plus usuels, les nombres rationnels, les nombres réels et les nombres complexes sont des corps parfaits.

  • Si un corps est de caractéristique nulle, alors il est parfait.

Ce ne sont néanmoins pas les uniques cas où une extension est séparable. La proposition suivante donne un exemple de séparabilité indépendamment de la caractéristique:

  • Soit L une extension de K et M une extension de L. Alors si M est une extension séparable de K, alors M est séparable sur L et L est séparable sur K.

Dans le cas où la caractéristique de K est égale à p, alors K est parfait si et seulement si tout élément de K possède une racine pième. On en déduit que:

  • Tout corps fini est parfait.

Ces propriétés sont démontrées dans l'article détaillé.

Propriétés

Morphisme dans la clôture algébrique

L'une des raisons essentielles de l'intérêt de la notion de séparabilité provient du nombre de morphisme de corps de L dans Ω laissant invariant K. Cette propriété est utilisée pour le théorème de l'élément primitif et pour de nombreuses propriétés des extensions galoisiennes. L'unique cas traité ici est celui ou L est une extension finie. Dans la suite de l'article, L est toujours supposé finie de dimension n. Le cas ou il existe un élément l générateur de l'extension est traité par la proposition suivante:

  • S'il existe un élément l tel que K(l) est égal à L alors il existe au plus n morphismes de L dans Ω. Si l est séparable, alors il existe exactement n morphismes.

Dans le cas général, c’est-à-dire sans hypothèse de séparabilité ni de simplicité de l'extension, une propriété analogue est toujours vraie.

  • Le nombre de morphismes de L dans Ω laissant invariant K est inférieur ou égal à n.s

Elle se démontre à l'aide de la propriété suivante:

  • Soit une famille finie de m morphismes de L dans Ω. Si les morphismes sont distincts deux à deux, alors la famille est libre.

Dans le cas particulier où l'extension est engendrée par des éléments séparables, l'hypothèse de simplicité de l'extension n'est pas nécessaire pour obtenir un résultat analogue à la première proposition:

  • Si L est engendré par des éléments séparables alors il existe exactement n morphismes de corps de L à valeur dans Ω laissant invariant K.

Pour la démonstration, les propositions suivantes sont utilisées :

  • Si L est une extension finie de K1 et K1 une extension de K, alors un morphisme de K1 dans Ω laissant invariant K se prolonge en un morphisme de L dans Ω laissant invariant K.
  • Si L est une extension de K1 contenant n1 morphismes de L dans Ω laissant invariant K1 et K1 une extension de K contenant n2 morphismes de K1 dans Ω laissant invariant K, alors il existe au moins n1.n2 morphismes de L dans Ω laissant invariant K.


Démonstrations
  • S'il existe un élément l tel que K(l) est égal à L alors il existe au plus n morphismes de L dans Ω laissant invariant K. Si l est séparable, alors il existe exactement n morphismes.

Soit P(X) le polynôme minimal de l dans K. La première proposition du paragraphe Extension algébrique et sur-corps indique, pour toute racine xi de P(X) dans Ω, l'existence d'un morphisme de L dans Ω qui à l associe xi. Il existe donc au moins autant de morphismes que de racines de P(X).

Réciproquement, si f est un morphisme de L dans Ω, alors P(f(l))=f(P(l)))=0. Donc l a pour image par f une racine.

En conclusion, il existe exactement autant de morphismes que de racines de P(X) dans Ω. Dans le cas général il n'existe donc jamais plus de morphismes que le degré de P(X), lequel est égal à la dimension de L. En effet, la famille (1, l, l2, ... , ln-1) est une base de L. Une condition nécessaire et suffisante d'égalité entre le nombre de morphismes et la dimension de L est la séparabilité de l.

  • Soit une famille finie de m morphismes de L dans Ω. Si les morphismes sont distincts deux à deux, alors la famille est libre en tant que partie d'un espace vectoriel de corps Ω.

Raisonnons par contraposée. Soit (fi) une famille linéairement dépendante de m morphisme, à une permutation près, on peut supposer que l'élément d'indice p est non nul, et combinaison linéaire des précédents qui forment une famille libre. l'égalité suivante est donc vérifiée:

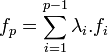
f_p=\sum_{i=1}^{p-1}\lambda_i.f_i\;

Si l et l' sont deux éléments de L tel que l' soit choisi non nul, alors fi(l.l')=fi(l)fi(l'). Comme fi(l') est non nul, l'égalité suivante est vérifiée:

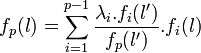
f_p(l)=\sum_{i=1}^{p-1}\frac{\lambda_i.f_i(l')}{f_p(l')}.f_i(l)\;

La famille des p-1 premiers éléments est choisie libre. La combinaison linéaire est unique, on en déduit les p-1 égalités suivantes.

\forall i \in [1, p-1]\quad \lambda_i.f_i(l')=\lambda_i.f_p(l')\;

Cette égalité est vrai pour tout l' d'où l'égalité entre fi et c si le scalaire associé est non nul. Il existe au moins un scalaire associé non nul car fp est non nul. Nous avons démontré que la famille n'est pas distincte deux à deux. La contraposée permet de terminer la démonstration.

  • Le nombre de morphismes de L dans Ω est inférieur ou égal à n.

Considérons E l'espace des applications K linéaires de L dans Ω. E est un espace vectoriel de dimension n sur le corps Ω. En effet, si (li) est une base de L l'application φ de E dans Ωn qui à une application linéaire m associe ((m(li)) est un isomorphisme d'espace vectoriel.

Considérons alors la famille de tous les morphismes de corps de L dans Ω. C'est une famille de E d'éléments distincts deux à deux. C'est donc une famille libre qui ne peut comporter plus d'éléments que la dimension de l'espace E. Et la proposition est démontrée.

  • Si L est une extension finie de K1 et K1 une extension de K. Alors un morphisme f de K1 dans Ω laissant invariant K se prolonge en un morphisme de L dans Ω laissant invariant K.

L est un espace vectoriel sur K1 il existe donc une base (l1, l2, ...,lm) où l1 = 1 de L sur K1.

Considérons alors l'application g de L dans Ω défini par l'application définie par:

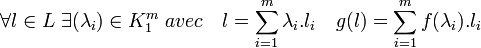
\forall l \in L \; \exist (\lambda_i) \in K_1^m \; avec \quad l=\sum_{i=1}^m \lambda_i.l_i \quad g(l)=\sum_{i=1}^m f(\lambda_i).l_i\;

Montrons alors que g est un morphisme de L dans Ω. Pour cela considérons un deuxième élément l' de coordonnées λi' dans la base considérée:

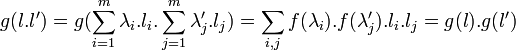
g(l.l')=g(\sum_{i=1}^m \lambda_i.l_i.\sum_{j=1}^m \lambda_j'.l_j)=\sum_{i,j}f(\lambda_i).f(\lambda_j').l_i.l_j=g(l).g(l') \;

Les égalités précédentes montrent que g est le morphisme cherché et la proposition est démontrée car le corps K est manifestement invariant.

  • Si L est une extension de K1 contenant n1 morphismes de L dans Ω laissant invariant K1 et K1 une extension de K contenant n2 morphismes de K1 dans Ω laissant invariant K. Alors il existe au moins n1.n2 morphismes de L dans Ω laissant invariant K.

La proposition précédente montre qu'il est possible d'étendre les morphismes de K1 à L. Il existe n1.n2 compositions différentes de morphismes. Il ne reste donc qu'à vérifier que ces morphismes sont tous distincts. Soit (mi) les n1 prolongements dans L des morphismes de K1 et (m'j) les n2 morphismes de L. Si mi est différent de mi' alors leurs composées avec des morphismes de la deuxième famille sont distinctes car elles sont distinctes sur K1.

Il suffit alors de montrer que les composés de mi avec deux morphismes différents m'j et m'j' sont distinctes. Si leurs images sont différentes, alors les composées sont distinctes car elles n'ont pas le même ensemble d'arrivée. Considérons le cas ou les images sont les mêmes. Alors la base de L de la proposition précédente a pour image par m'j une base B' de l'ensemble d'arrivée de m'j et m'j'. Soit l un élément de L ayant deux images différentes par m'j et m'j'. Il existe alors un élément de la base B' tel que les coefficients a et a' des images par les deux morphismes sont différents. D'après la construction de l'extension décrite durant la démonstration précédente, les coefficients des composées sont alors mi(a) et mi(a') qui sont différents car mi est injectif comme tous les morphismes de corps. Et la proposition est démontrée.

  • Si L est engendré par des éléments séparables alors il existe exactement n morphismes de corps de L à valeur dans Ω laissant invariant K.

Montrons la proposition suivante par récurrence sur m:

Si une extension finie L d'un corps Ki est générée par m éléments de L, alors le nombres de morphismes de L dans Ω laissant invariant Ki au moins égal à la dimension de L sur Ki.

Si m est égal à 0, la proposition est trivialement vraie. Supposons le résultat vrai pour m est supposons que L est généré par une famille (li) de m+1 éléments. Notons alors K1 l'extension de K K(lm+1). L est alors une extension de K(lm+1) générée par m éléments séparables. L est une extension de K(lm+1) générée par m éléments, l'hypothèse de récurrence montre qu'il existe au moins la dimension de L sur K(lm+1) (que l'on note [L:K(lm+1)]) morphismes de L dans Ω laissant invariant K(lm+1). Nous avons démontré qu'il existe [K(lm+1):K] morphismes de K(lm+1) dans Ω laissant invariant K. La proposition précédente montre donc qu'ils existes au moins [L:K(lm+1)].[K(lm+1):K] morphismes de L dans Ω laissant invariant K. Or ce produit est égal à la [L:K] d'après une proposition élémentaire démontrée dans l'article Extension algébrique.

Donc si L est séparable, il existe au moins n morphismes. Or une proposition précédente montre qu'il en existe dans le cas général au plus n. La démonstration est donc terminée.

Théorème de l'élément primitif

Article détaillé : Théorème de l'élément primitif.

Toutes les propriétés du paragraphe précédent peuvent se résumer par le fait que, dans le contexte des extensions finies L sur K, la séparabilité implique que le nombre de morphismes est égal à la dimension de L sur K. Une analyse plus fine montre que les deux propriétés sont équivalentes. Ces deux propriétés sont aussi équivalente à une troisième: l'extension est engendrée par un unique élément séparable. Ainsi, pour une famille importante de corps, celle des corps parfaits contenant non seulement les corps usuels mais aussi tous les corps finis, toute extension finie est non seulement séparable, mais il existe autant de morphismes que la dimension de l'extension et l'extension est simple. Ce résultat se résume dans par un théorème fondamental pour la théorie de Galois, connu sous le nom de l'élément primitif.

  • Les quatre conditions suivantes sont équivalentes:
  1. L'extension L est séparable sur K.
  2. L'extension est engendrée par des éléments séparables.
  3. Il existe exactement n morphismes de L dans Ω laissant invariant K.
  4. L est une extension simple générée par un élément séparable.

La démonstration est donnée dans l'article détaillé.

Forme trace

Article détaillé : forme trace.

Il existe un critère nécessaire et suffisant pour qu'une extension finie soit séparable, elle utilise la forme trace, une forme bilinéaire de L. Soit φ l'application qui à a associe l'endomorphisme φa défini par :

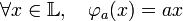
\forall x \in \mathbb L,\quad \varphi_a(x) = ax \;

La forme trace associe à deux éléments a et b de L la trace de l'endomorphisme φab.

  • L'extension L est séparable sur K si et seulement si la forme trace est non dégénérée.

La démonstration est donnée dans l'article détaillé.

Voir aussi

Liens externes

Références

R. et A. Douady Algèbre et théories galoisiennes Cedic/Fernand Nathan 1978
S. Lang Algebre Dunod 2004
P. Samuel Théorie algébrique des nombres Hermann Paris 1971
Articles de mathématiques en rapport avec la théorie de Galois
Corps Corps fini · Corps parfait · Corps de rupture · Corps de décomposition
Extension de corps Extension algébrique · Extension quadratique · Extension simple · Extension normale · Extension séparable · Extension de Galois · Groupe de Galois · Clôture algébrique
Articles associés Caractéristique · Polynôme formel · Polynôme cyclotomique · Théorie de Galois · Théorème fondamental de la théorie de Galois · Théorème de l'élément primitif · Théorie d'Iwasawa
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Extension s%C3%A9parable ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Extension Séparable de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Extension separable — Extension séparable Une extension algébrique L d un corps K est dite séparable si et seulement si le polynôme minimal de tout élément de L n admet que des racines simples. Ce critère est une hypothèse nécessaire pour établir un théorème important …   Wikipédia en Français

  • Extensión separable — Saltar a navegación, búsqueda En matemáticas, una extensión separable de un cuerpo K es un cuerpo L que contiene a K y que puede ser generado adjuntando a K un conjunto de elementos α, tales que son raíces de polinomios separables sobre K. En… …   Wikipedia Español

  • Extension séparable — Une extension algébrique L d un corps K est dite séparable si le polynôme minimal de tout élément de L n admet que des racines simples (dans une clôture algébrique de K). La séparabilité est une des propriétés des extensions de Galois. Toute… …   Wikipédia en Français

  • Extension De Galois — En mathématiques, une extension de Galois (parfois nommée extension galoisienne) est une extension de corps finie normale séparable. L ensemble des automorphismes de l extension possède une structure de groupe appelé groupe de Galois. Cette… …   Wikipédia en Français

  • Extension de galois — En mathématiques, une extension de Galois (parfois nommée extension galoisienne) est une extension de corps finie normale séparable. L ensemble des automorphismes de l extension possède une structure de groupe appelé groupe de Galois. Cette… …   Wikipédia en Français

  • Extension galoisienne — Extension de Galois En mathématiques, une extension de Galois (parfois nommée extension galoisienne) est une extension de corps finie normale séparable. L ensemble des automorphismes de l extension possède une structure de groupe appelé groupe de …   Wikipédia en Français

  • Extension Simple — En mathématiques et plus précisément en algèbre dans le cas de la théorie de Galois, une extension de corps L d un corps K est dite simple si et seulement s il existe un élément l de L tel que L est égal à K[l]. Une extension simple est finie si… …   Wikipédia en Français

  • Extension Quadratique — En mathématiques, et plus précisément en algèbre dans le cadre de la théorie de Galois, une extension quadratique est une extension de corps de dimension deux. Si K est un corps commutatif, souvent celui des nombres rationnels, alors une… …   Wikipédia en Français

  • Extension Normale — En mathématiques, une extension normale L de K est un cas particulier d extension de corps. Une extension est dite normale si et seulement si tout morphisme de corps laissant invariant K est un automorphisme de L. Cette propriété est utilisée… …   Wikipédia en Français

  • Extension De Corps — En mathématiques, plus particulièrement en algèbre, l extension d un corps K est un corps L qui contient K comme sous corps. Par exemple, , le corps des nombres complexes, est une extension de , le corps des nombres réels, lequel est lui même un… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”