Transposition (algèbre)
- Transposition (algèbre)
-
Matrice transposée
La matrice transposée (on dit aussi la transposée) d'une matrice 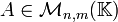 est la matrice notée
est la matrice notée 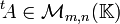 (parfois aussi notée AT,
(parfois aussi notée AT, 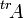 ou A * ), obtenue en échangeant les lignes et les colonnes de A.
ou A * ), obtenue en échangeant les lignes et les colonnes de A.
La première notation, avec le t avant le nom de la matrice, est la notation utilisée en France, celle où le t se situe après le nom de la matrice à transposer est une notation américaine. Il est donc préférable de savoir d'où proviennent les exercices !
Si 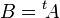 , alors
, alors ![\forall {(i,j) \in [\![1;m]\!]\times[\![1;n]\!]}, b_{i,j} = a_{j,i}\,](/pictures/frwiki/99/ca56778bfdba016086ffa96eb0ecf591.png) .
.
Exemple : 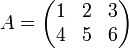 alors
alors 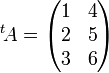
Propriétés
Démonstration
t est linéaire (revenir à la définition). De plus, 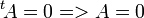 , donc t est injective. Les espaces de départ et d'arrivée sont les mêmes (et ont la même dimension nm), donc c'est un isomorphisme.
, donc t est injective. Les espaces de départ et d'arrivée sont les mêmes (et ont la même dimension nm), donc c'est un isomorphisme.
- La transposée de la somme de deux matrices est égale à la somme des transposées de ces deux matrices :
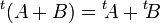
- La transposée du produit de deux matrices est égale au produit inversé des transposées de ces deux matrices :
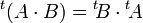
- La transposée de l'inverse d'une matrice carrée est égale à l'inverse de la transposée de cette même matrice :
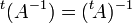
- Si A désigne une matrice carrée de dimension n et B sa transposée, alors
![\forall {i \in [\![1;n]\!]}, b_{i,i} = a_{i,i}\,](/pictures/frwiki/101/e0fc654894c73ff284640d3d2de453f3.png) .
.
- Une matrice égale à sa transposée est appelée matrice symétrique.
Interprétation : dualité
Si A représente une application linéaire par rapport à deux bases, alors sa transposée 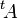 représente la matrice de la transposée de l'application par rapport aux bases duales (voir espace dual).
représente la matrice de la transposée de l'application par rapport aux bases duales (voir espace dual).
Dans le cadre des espaces euclidiens, si A représente une application linéaire par rapport à deux bases orthonormales, alors sa transposée 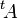 représente la matrice de l'application adjointe.
représente la matrice de l'application adjointe.
Voir aussi
|
Articles en rapport avec les matrices |
| Par forme |
|
| Transformée |
|
| En relation |
|
| Par propriété |
|
| Par famille |
|
| Particulière |
|
| Associée |
|
| Résultats |
|
| Voir aussi |
|
 Portail des mathématiques
Portail des mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Transposition (algèbre) de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Algebre de Clifford — Algèbre de Clifford En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l une des… … Wikipédia en Français
Algèbre De Clifford — En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l une des généralisations possibles des… … Wikipédia en Français
Algèbre de Clifford du plan euclidien) — Algèbre de Clifford En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l une des… … Wikipédia en Français
Algèbre de clifford — En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l une des généralisations possibles des… … Wikipédia en Français
Algèbre de Clifford — Pour les articles homonymes, voir Algèbre (homonymie). En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être… … Wikipédia en Français
Transposition — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « transposition », sur le Wiktionnaire (dictionnaire universel) « transposer », sur le… … Wikipédia en Français
transposition — (tran spô zi sion ; en vers, de cinq syllabes) s. f. 1° Action de transposer ; résultat de cette action. • Ces transpositions d épîtres [d un Mécène à un autre] sont arrivées plus d une fois ; et un homme du Dauphiné ayant fait le panégyrique … Dictionnaire de la Langue Française d'Émile Littré
Transposition (mathématiques) — Matrice transposée La matrice transposée (on dit aussi la transposée) d une matrice est la matrice notée (parfois aussi notée AT, ou A * ), obtenue en échangeant les lignes et les colonnes de A. La première notation, avec le t avant le nom de la… … Wikipédia en Français
Transposition matricielle — Matrice transposée La matrice transposée (on dit aussi la transposée) d une matrice est la matrice notée (parfois aussi notée AT, ou A * ), obtenue en échangeant les lignes et les colonnes de A. La première notation, avec le t avant le nom de la… … Wikipédia en Français
LINÉAIRE ET MULTILINÉAIRE (ALGÈBRE) — LINЙAIRE ET MULTILINЙAIRE (ALGИBRE) L’algèbre linéaire sur un corps commutatif, telle qu’on la trouvera présentée ici, s’est progressivement dégagée, au cours du XIXe siècle et au début du XXe, de la théorie des équations linéaires (systèmes de n … Encyclopédie Universelle
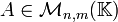 est la matrice notée
est la matrice notée 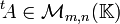 (parfois aussi notée AT,
(parfois aussi notée AT, 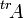 ou A * ), obtenue en échangeant les lignes et les colonnes de A.
ou A * ), obtenue en échangeant les lignes et les colonnes de A.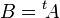 , alors
, alors ![\forall {(i,j) \in [\![1;m]\!]\times[\![1;n]\!]}, b_{i,j} = a_{j,i}\,](/pictures/frwiki/99/ca56778bfdba016086ffa96eb0ecf591.png) .
.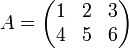 alors
alors 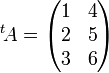
 est un isomorphisme ( application bijective )
est un isomorphisme ( application bijective )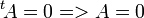 , donc t est injective. Les espaces de départ et d'arrivée sont les mêmes (et ont la même dimension nm), donc c'est un isomorphisme.
, donc t est injective. Les espaces de départ et d'arrivée sont les mêmes (et ont la même dimension nm), donc c'est un isomorphisme.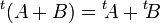
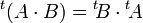
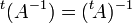
![\forall {i \in [\![1;n]\!]}, b_{i,i} = a_{i,i}\,](/pictures/frwiki/101/e0fc654894c73ff284640d3d2de453f3.png) .
.
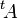 représente la matrice de la transposée de l'application par rapport aux bases duales (voir espace dual).
représente la matrice de la transposée de l'application par rapport aux bases duales (voir espace dual).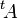 représente la matrice de l'application adjointe.
représente la matrice de l'application adjointe.