Transposition (mathématiques)
- Transposition (mathématiques)
-
Matrice transposée
La matrice transposée (on dit aussi la transposée) d'une matrice 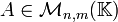 est la matrice notée
est la matrice notée 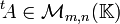 (parfois aussi notée AT,
(parfois aussi notée AT, 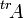 ou A * ), obtenue en échangeant les lignes et les colonnes de A.
ou A * ), obtenue en échangeant les lignes et les colonnes de A.
La première notation, avec le t avant le nom de la matrice, est la notation utilisée en France, celle où le t se situe après le nom de la matrice à transposer est une notation américaine. Il est donc préférable de savoir d'où proviennent les exercices !
Si 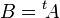 , alors
, alors ![\forall {(i,j) \in [\![1;m]\!]\times[\![1;n]\!]}, b_{i,j} = a_{j,i}\,](/pictures/frwiki/99/ca56778bfdba016086ffa96eb0ecf591.png) .
.
Exemple : 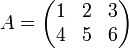 alors
alors 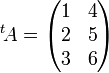
Propriétés
Démonstration
t est linéaire (revenir à la définition). De plus, 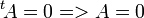 , donc t est injective. Les espaces de départ et d'arrivée sont les mêmes (et ont la même dimension nm), donc c'est un isomorphisme.
, donc t est injective. Les espaces de départ et d'arrivée sont les mêmes (et ont la même dimension nm), donc c'est un isomorphisme.
- La transposée de la somme de deux matrices est égale à la somme des transposées de ces deux matrices :
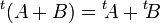
- La transposée du produit de deux matrices est égale au produit inversé des transposées de ces deux matrices :
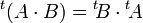
- La transposée de l'inverse d'une matrice carrée est égale à l'inverse de la transposée de cette même matrice :
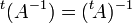
- Si A désigne une matrice carrée de dimension n et B sa transposée, alors
![\forall {i \in [\![1;n]\!]}, b_{i,i} = a_{i,i}\,](/pictures/frwiki/101/e0fc654894c73ff284640d3d2de453f3.png) .
.
- Une matrice égale à sa transposée est appelée matrice symétrique.
Interprétation : dualité
Si A représente une application linéaire par rapport à deux bases, alors sa transposée 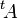 représente la matrice de la transposée de l'application par rapport aux bases duales (voir espace dual).
représente la matrice de la transposée de l'application par rapport aux bases duales (voir espace dual).
Dans le cadre des espaces euclidiens, si A représente une application linéaire par rapport à deux bases orthonormales, alors sa transposée 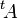 représente la matrice de l'application adjointe.
représente la matrice de l'application adjointe.
Voir aussi
|
Articles en rapport avec les matrices |
| Par forme |
|
| Transformée |
|
| En relation |
|
| Par propriété |
|
| Par famille |
|
| Particulière |
|
| Associée |
|
| Résultats |
|
| Voir aussi |
|
 Portail des mathématiques
Portail des mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Transposition (mathématiques) de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
MATHÉMATIQUES (DIDACTIQUE DES) — Les problèmes posés par l’enseignement des mathématiques ne sont pas nouveaux. Au début du siècle, Henri Lebesgue était préoccupé par les conditions de l’enseignement et de la formation des professeurs. Des efforts plus récents se sont déployés… … Encyclopédie Universelle
Mathematiques du Sudoku — Mathématiques du Sudoku Grille de Sudoku classique … Wikipédia en Français
Mathématiques Du Sudoku — Grille de Sudoku classique … Wikipédia en Français
Mathématiques du sudoku — Grille de Sudoku classique … Wikipédia en Français
transposition — [ trɑ̃spozisjɔ̃ ] n. f. • v. 1370; de transposer 1 ♦ Changement de place, et spécialt(XVIe) Interversion. « Par une transposition de sens, M. de Cambremer vous regardait avec son nez » (Proust). Pathol. Transposition vasculaire : anomalie… … Encyclopédie Universelle
Mathématiques du Sudoku — Grille de Sudoku classique Variante du Sudoku basée sur des comparaisons entre les cases … Wikipédia en Français
Transposition — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « transposition », sur le Wiktionnaire (dictionnaire universel) « transposer », sur le… … Wikipédia en Français
Transposition (algèbre) — Matrice transposée La matrice transposée (on dit aussi la transposée) d une matrice est la matrice notée (parfois aussi notée AT, ou A * ), obtenue en échangeant les lignes et les colonnes de A. La première notation, avec le t avant le nom de la… … Wikipédia en Français
Transposition matricielle — Matrice transposée La matrice transposée (on dit aussi la transposée) d une matrice est la matrice notée (parfois aussi notée AT, ou A * ), obtenue en échangeant les lignes et les colonnes de A. La première notation, avec le t avant le nom de la… … Wikipédia en Français
Tenseur (mathématiques) — Pour l’article homonyme, voir Tenseur. Les tenseurs sont des objets mathématiques issus de l algèbre multilinéaire permettant de généraliser les scalaires et les vecteurs. On les rencontre notamment en analyse vectorielle et en… … Wikipédia en Français
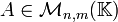 est la matrice notée
est la matrice notée 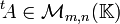 (parfois aussi notée AT,
(parfois aussi notée AT, 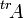 ou A * ), obtenue en échangeant les lignes et les colonnes de A.
ou A * ), obtenue en échangeant les lignes et les colonnes de A.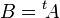 , alors
, alors ![\forall {(i,j) \in [\![1;m]\!]\times[\![1;n]\!]}, b_{i,j} = a_{j,i}\,](/pictures/frwiki/99/ca56778bfdba016086ffa96eb0ecf591.png) .
.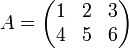 alors
alors 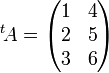
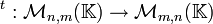 est un isomorphisme ( application bijective )
est un isomorphisme ( application bijective )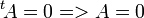 , donc t est injective. Les espaces de départ et d'arrivée sont les mêmes (et ont la même dimension nm), donc c'est un isomorphisme.
, donc t est injective. Les espaces de départ et d'arrivée sont les mêmes (et ont la même dimension nm), donc c'est un isomorphisme.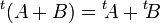
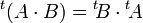
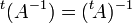
![\forall {i \in [\![1;n]\!]}, b_{i,i} = a_{i,i}\,](/pictures/frwiki/101/e0fc654894c73ff284640d3d2de453f3.png) .
.
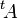 représente la matrice de la transposée de l'application par rapport aux bases duales (voir espace dual).
représente la matrice de la transposée de l'application par rapport aux bases duales (voir espace dual).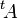 représente la matrice de l'application adjointe.
représente la matrice de l'application adjointe.