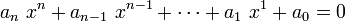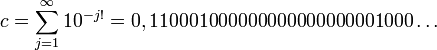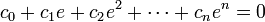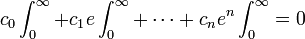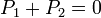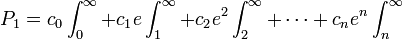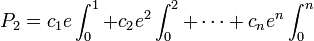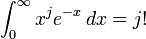Transcendance mathématique

Nombre transcendant

En mathématiques, un nombre transcendant est un nombre réel ou complexe qui n'est racine d'aucune équation polynomiale :

$a_n~x^n + a_{n-1}~x^{n-1} + \cdots + a_1~x^1 + a_0 = 0\,$

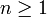où $n \ge 1\,$ et les coefficients 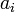$a_i\,$ sont des nombres entiers (donc des rationnels), dont au moins l'un $a n$ est non nul. Un nombre réel ou complexe est donc transcendant si et seulement s’il n'est pas algébrique.

Les nombres transcendants ne sont jamais rationnels. Néanmoins, tous les nombres irrationnels ne sont pas transcendants : la racine carrée de 2 est irrationnelle, mais est une solution de l'équation polynomiale $x^2 - 2 = 0\,$ .

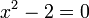L'ensemble de tous les nombres transcendants est non dénombrable. La preuve est simple : puisque les polynômes à coefficients entiers sont dénombrables, et puisque chacun de ces polynômes possède un nombre fini de zéros, l'ensemble des nombres algébriques est dénombrable. Mais l'argument de la diagonale de Cantor établit que les nombres réels (et par conséquent les nombres complexes aussi) sont non dénombrables, donc l'ensemble de tous les nombres transcendants doit être non dénombrable. En d'autres termes, il y a beaucoup plus de nombres transcendants que de nombres algébriques. Néanmoins, seules peu de classes de nombres transcendants sont connues et prouver qu'un nombre donné est transcendant peut être extrêmement difficile.

Résultats : considérons l'ensemble A des nombres algébriques réels. Alors :

A est un sous-corps de 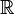$\mathbb{R}\,$ . En particulier, A est stable par addition et multiplication.
A est dénombrable, ce qui montre que A est différent de l'ensemble 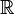$\mathbb{R}\,$ (les nombres transcendants existent bien).

Sommaire

1 Histoire
2 Quelques nombres transcendants connus
3 Problèmes ouverts
4 Esquisse de démonstration de la transcendance de e
5 Voir aussi
6 Références
7 Liens externes

Histoire

Leibniz fut probablement la première personne à croire en l'existence des nombres qui ne satisfont pas les polynômes à coefficients rationnels. Le nom « transcendants » vient de Leibniz dans sa publication de 1682 où il démontra que sin(x) n'est pas une fonction algébrique de x. L'existence des nombres transcendants fut prouvée pour la première fois en 1844 par Joseph Liouville, qui montra des exemples, incluant la constante de Liouville :

$c = \sum_{j=1}^\infty 10^{-j!} = 0,110001000000000000000001000\ldots$

dans lequel le n-ième chiffre après la virgule est 1 si n est une factorielle (l'un des nombres 1, 2, 6, 24, 120, 720, etc.) et 0 sinon ; ce nombre est particulièrement bien approché par les nombres rationnels. Joseph Liouville montra que les nombres ayant cette propriété (que nous nommons maintenant nombres de Liouville) sont tous transcendants ; on trouvera cette démonstration à l'article consacré à ces nombres.

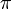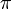Johann Heinrich Lambert, dans son article prouvant l'irrationalité de $\pi\,$ conjectura que $e\,$ et $\pi\,$ étaient des nombres transcendants. Le premier nombre à avoir été démontré transcendant sans avoir été construit spécialement pour cela fut e, par Charles Hermite en 1873. En 1874, Georg Cantor trouva l'argument décrit ci-dessus établissant l'ubiquité des nombres transcendants.

En 1882, Ferdinand von Lindemann publia une démonstration de la transcendance de 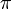$\pi\,$ . Il montra d'abord que $e$ à n'importe quelle puissance algébrique non nulle est transcendant, et puisque 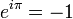$e^{i\pi} = -1\,$ est algébrique (voir identité d'Euler), 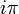$i\pi\,$ et par conséquent 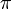$\pi\,$ doit être transcendant. Cette approche fut généralisée par Karl Weierstrass avec le théorème de Lindemann-Weierstrass. La transcendance de 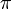$\pi\,$ a permis la démonstration de l'impossibilité de plusieurs constructions géométriques anciennes avec le compas et la règle, incluant le plus célèbre d'entre eux, la quadrature du cercle.

En 1900, David Hilbert a posé une importante question à propos des nombres transcendants, connue sous le nom de septième problème de Hilbert : « Si a est un nombre algébrique non nul et différent de 1 et si b est un nombre algébrique irrationnel, alors le nombre 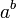$a^b\,$ est-il nécessairement transcendant ? » La réponse, affirmative, fut donnée en 1934 par le théorème de Gelfond-Schneider. 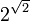On peut obtenir facilement des nombres transcendants grâce à lui, par exemple $2^{\sqrt{2}}\,$ .

Ce travail fut étendu par Alan Baker dans les années 1960.

Quelques nombres transcendants connus

Le nombre 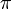$\pi\,$ (voir l'article pi).
Le nombre e (base des logarithmes néperiens)
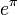$e^{\pi}\,$ constante de Gelfond
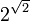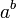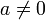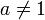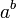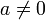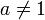$2^{\sqrt{2}}\,$ (constante de Gelfond-Schneider) ou plus généralement $a^b\,$ (voir le théorème de Gelfond-Schneider) où $a \ne 0\,$ et $a\ne 1\,$ est algébrique et b est algébrique mais non rationnel. Le cas général du septième problème de Hilbert, c’est-à-dire déterminer si $a^b\,$ est transcendant lorsque $a \ne 0\,$ et $a\ne 1\,$ est algébrique et b est irrationnel, reste non résolu.
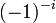$(-1)^{-i}\,$ (qui est le nombre réel $e π$ ) pour la raison exposée ci-dessus.
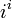$i^i\,$ qui est le nombre réel $e - π / 2$ .
La valeur de la fonction trigonométrique $\sin(1)\,$
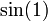
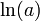$\ln(a)\,$ si a est un rationnel strictement positif et différent de 1.
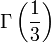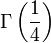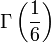$\Gamma\left(\frac{1}{3}\right)\,$ , $\Gamma\left(\frac{1}{4}\right)\,$ et $\Gamma\left(\frac{1}{6}\right)\,$ (voir fonction Gamma d'Euler).
Le nombre de Champernowne 0,12345678910111213… obtenu en écrivant à la suite les nombres entiers en base dix (théorème de Mahler, 1961)
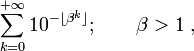
$\sum_{k=0}^{+\infty} 10^{-\lfloor \beta^{k} \rfloor};\qquad \beta > 1\; ,$

où 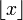$\ \lfloor x \rfloor$ est la partie entière de 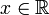$\ x \in \mathbb{R}$ . Par exemple, si 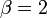$\beta = 2\,$ , ce nombre est 0,11010001000000010000000000000001000…

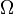$\Omega\,$ , constante de Chaitin, et plus généralement : chaque nombre non-calculable est transcendant (puisque tous les nombres algébriques sont calculables).

constante de Prouhet-Thue-Morse

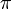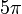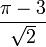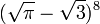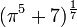Toute fonction algébrique non constante à une variable donne une valeur transcendante lorsqu'on lui applique une valeur transcendante. Donc, par exemple, en sachant que $\pi\,$ est transcendant, nous pouvons immédiatement déduire que $5\pi\,$ , $\frac{\pi-3}{\sqrt{2}}\,$ , $(\sqrt{\pi}-\sqrt{3})^8\,$ et $(\pi^{5}+7)^{\frac{1}{7}}\,$ sont aussi transcendants.

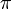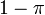Néanmoins, une fonction algébrique à plusieurs variables peut donner un nombre algébrique lorsqu'elle est appliquée aux nombres transcendants si ces nombres ne sont pas algébriquement indépendants. Par exemple, $\pi\,$ et $1-\pi\,$ sont tous les deux transcendants, mais 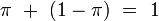$\pi~+~(1-\pi)~=~1\,$ ne l'est évidemment pas. 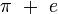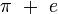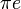On ignore si $\pi~+~e\,$ , par exemple est transcendant, mais au moins l'un des deux nombres $\pi~+~e\,$ et $\pi e\,$ doit être transcendant. Plus généralement, pour deux nombres transcendants a et b, au moins l'un de a+b et a b doit être transcendant. Pour voir cela, considérons le polynôme 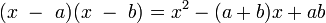$(x~-~a) (x~-~b) = x^2 - (a+b) x + a b\,$ ; si (a+b) et a b étaient tous deux algébriques, alors ce polynôme serait à coefficients algébriques. Comme les nombres algébriques forment un corps algébriquement clos, ceci impliquerait que les racines du polynôme, a et b soient algébriques. Mais ceci est une contradiction et ainsi, au moins un des deux coefficients est transcendant.

Problèmes ouverts

Les nombres dont on ignore s'ils sont transcendants ou non incluent :

$(\pi~+~e)\,$ , $(\pi~-~e)\,$ , $(\pi e)\,$ , $\left(\frac{e}{\pi}\right)\,$ , $(\pi^{\pi})\,$ , $(e^e)\,$ , $(\pi^e)\,$

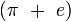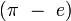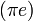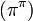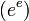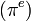
La constante d'Euler-Mascheroni 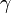$\gamma\,$ (dont on ignore même si elle est irrationnelle)

La constante de Catalan (dont on ignore aussi si elle est irrationnelle)

La constante d'Apéry 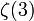$\zeta(3)\,$ (dont on sait qu'elle est irrationnelle)

Tous les nombres de Liouville sont transcendants, néanmoins les nombres transcendants ne sont pas tous des nombres de Liouville. Tout nombre de Liouville doit avoir des termes non bornés dans son développement en fraction continue, donc en utilisant un argument de dénombrement, on peut montrer qu'il existe des nombres transcendants qui ne sont pas des nombres de Liouville. En utilisant le développement explicite en fraction continue de e, on peut montrer que e n'est pas un nombre de Liouville. Kurt Mahler montra en 1953 que 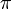$\pi\,$ n'est pas non plus un nombre de Liouville. Il a été conjecturé que toutes les fractions continues à termes bornés qui ne sont pas périodiques à partir d'un certain rang sont transcendantes (les fractions continues périodiques à partir d'un certain rang correspondent aux irrationnels quadratiques).

Esquisse de démonstration de la transcendance de $e$

La première démonstration que $e$ est transcendant date de 1873. Nous suivrons maintenant la stratégie de David Hilbert (1862 - 1943) qui donna une simplification de la démonstration originale de Charles Hermite. L'idée est la suivante :

Supposons, dans le but de trouver une contradiction, que $e$ est algébrique. Alors, il existe un ensemble fini de coefficients entiers 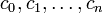$c_{0},c_{1},\ldots,c_{n}\,$ satisfaisant l'équation :

$c_{0}+c_{1}e+c_{2}e^{2}+\cdots+c_{n}e^{n}=0\,$

et $c 0$ et $c n$ sont tous deux différents de zéro.

Dépendant de la valeur de n, nous précisons un entier positif suffisamment grand k (pour nos besoin ultérieurs) et multiplions les deux cotés de l'équation ci-dessus par 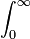$\int^{\infty}_{0}\,$ , où la notation 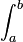$\int^{b}_{a}\,$ sera utilisé dans cette démonstration comme abréviation de l'intégrale :

$\int^{b}_{a}:=\int^{b}_{a}x^{k}[(x-1)(x-2)\cdots(x-n)]^{k+1}e^{-x}\,dx\,$ .

Nous arrivons à l'équation :

$c_{0}\int^{\infty}_{0}+c_{1}e\int^{\infty}_{0}+\cdots+c_{n}e^{n}\int^{\infty}_{0} = 0\,$

qui peut maintenant être écrite sous la forme

$P_{1}+P_{2}=0\,$

où

$P_{1}=c_{0}\int^{\infty}_{0}+c_{1}e\int^{\infty}_{1}+c_{2}e^{2}\int^{\infty}_{2}+\cdots+c_{n}e^{n}\int^{\infty}_{n}\,$

$P_{2}=c_{1}e\int^{1}_{0}+c_{2}e^{2}\int^{2}_{0}+\cdots+c_{n}e^{n}\int^{n}_{0}\,$

Le plan d'attaque maintenant est de montrer que pour un k suffisamment grand, les relations ci-dessus sont impossible à satisfaire parce que

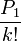$\frac{P_{1}}{k!}\,$ est un entier différent de zéro et 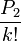$\frac{P_{2}}{k!}\,$ ne l'est pas.

Le fait que 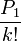$\frac{P_{1}}{k!}\,$ soit un entier différent de zéro résulte de la relation

$\int^{\infty}_{0}x^{j}e^{-x}\,dx=j!\,$

qui est valide pour tout entier positif j et peut être prouvé par récurrence au moyen d'une intégration par parties.

Pour montrer que

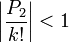$\left|\frac{P_{2}}{k!}\right|<1\,$ pour un k suffisamment grand

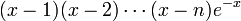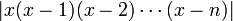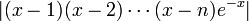nous noterons d'abord que $x^{k}[(x-1)(x-2)\cdots(x-n)]^{k+1}e^{-x}\,$ est le produit des fonctions $[x(x-1)(x-2)\cdots(x-n)]^{k}\,$ et $(x-1)(x-2)\cdots(x-n)e^{-x}\,$ . En utilisant la borne supérieure pour $|x(x-1)(x-2)\cdots(x-n)|\,$ et $|(x-1)(x-2)\cdots(x-n)e^{-x}|\,$ sur l'intervalle [0,n] et en employant le fait que

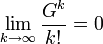$\lim_{k\to\infty}\frac{G^k}{k!}=0\,$ pour chaque nombre réel G

est alors suffisant pour achever la démonstration.

Une stratégie similaire, différente de l'approche originale de Lindemann, peut être utilisée pour montrer que le nombre 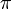$\pi\,$ est transcendant. En outre, la fonction gamma, certaines estimations pour $e$ et des faits à propos des polynômes symétriques jouent un rôle vital dans la démonstration.

Pour des informations détaillées concernant les démonstrations de transcendances de 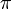$\pi\,$ et $e\,$ , voir les références et les liens externes.

Voir aussi

théorie de la transcendance, l'étude des questions relatives aux nombres transcendants

Références

(de) David Hilbert, « Über die Transcendenz der Zahlen $e$ und $π$ », Mathematische Annalen 43:216–219 (1893).
(en) Alan Baker, Transcendental Number Theory, Cambridge University Press, 1975 (ISBN 0-521-39791-X).

Liens externes

(fr) Article du 13 mai 1844 de Liouville sur les nombres transcendants (avec une analyse de M. Mendès-France, mathématicien) (site BibNum)
(fr) Démonstration d'Hermite de la transcendance de e (1873), présentée et analysée sur le site BibNum.
(en) Démonstration que $e$ est transcendant
[pdf] (de) Démonstration que $e$ est transcendant
[pdf] (de) Démonstration que $π$ est transcendant
[pdf] (fr) Démonstration de la transcendance de e et $π$
[pdf] (fr) Démonstration de la transcendance de e et $π$

Notion de nombre
Ensembles usuels	$\mathbb{N}$ Entier naturel • $\mathbb{Z}$ Entier relatif • $\mathbb{D}$ Nombre décimal • $\mathbb{Q}$ Nombre rationnel • $\mathbb{R}$ Nombre réel • $\mathbb{C}$ Nombre complexe
Extensions	$\mathbb{H}$ Quaternion • $\mathbb{O}$ Octonion • $\mathbb{S}$ Sédénion • Nombre complexe fendu • Tessarine • Nombre bicomplexe • Nombre multicomplexe • Biquaternion • Coquaternion • Octonion fendu • Nombre hypercomplexe • $\mathbb{Q}_p$ Nombre p-adique • Nombre hyperréel • Nombre superréel • Nombre dual • Droite réelle achevée • Nombre cardinal • Nombre ordinal • Nombre surréel et pseudo-réel
Propriétés particulières	Parité • Nombre premier • Nombre composé • Carré parfait • Nombre parfait • Nombre positif • Nombre négatif • Fraction dyadique • Nombre irrationnel • Nombre algébrique • Nombre transcendant • Nombre imaginaire pur • Nombre de Liouville • Nombre normal • Nombre univers • Nombre constructible • Nombre réel calculable • Nombre transfini • Infiniment petit • Infiniment grand
Exemples d’importance historique	π Pi • √2 Racine carrée de deux • φ Nombre d’or • 0 Zéro • $i$ Unité imaginaire • $e$ Constante de Neper • ℵ₀ Aleph-zéro • Table de constantes mathématiques
Notions connexes	Chiffre • Numération • Fraction • Opération • Calcul • Algèbre • Arithmétique • Suite d’entiers • ∞ Infini • Chiffre significatif

Portail des mathématiques

Ce document provient de « Nombre transcendant ».

Catégorie : Nombre transcendant

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Transcendance mathématique de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Constante mathématique e — e (nombre) Article d une série sur la constante mathématique e … Wikipédia en Français
FORME — L’histoire du concept de forme et des théories de la forme est des plus singulières. Nous vivons dans un monde constitué de formes naturelles. Celles ci sont omniprésentes dans notre environnement et dans les représentations que nous nous en… … Encyclopédie Universelle
HILBERT (PROBLÈMES DE) — «Qui ne se réjouirait de pouvoir soulever le voile qui cache le futur, de jeter un regard sur le développement des mathématiques, ses progrès ultérieurs, les secrets des découvertes des siècles à venir?...» Prévoir le futur des mathématiques: qui … Encyclopédie Universelle
ONTOLOGIE — «Ontologie» veut dire: doctrine ou théorie de l’être. Cette simple définition, toute nominale d’ailleurs, propose une petite énigme de lexique: le mot «ontologie» est considérablement plus récent que la discipline qu’il désigne; ce sont les Grecs … Encyclopédie Universelle
ARISTOTE — n’est sans doute pas le philosophe le plus séduisant de l’Antiquité, celui auquel on se reporte le plus volontiers quand on veut remonter aux sources de ce que les Grecs ont nommé la «sagesse». Mais nul n’a marqué autant que lui la philosophie et … Encyclopédie Universelle
Pi — Pour les articles homonymes, voir Pi (homonymie). Si le diamètre du cercle est 1, sa circonférence est π. Pi[1 … Wikipédia en Français
Histoire Des Mathématiques — Article de la série Histoire des sciences Chronologie Chronologie des sciences Chronologie de l astronomie … Wikipédia en Français
Histoire des mathematiques — Histoire des mathématiques Article de la série Histoire des sciences Chronologie Chronologie des sciences Chronologie de l astronomie … Wikipédia en Français
Histoire des mathématiques — L’histoire des mathématiques s étend sur plusieurs millénaires et dans de nombreuses régions du globe allant de la Chine à l’Amérique centrale. Jusqu au XVIIe siècle, le développement des connaissances mathématiques s’effectue… … Wikipédia en Français
Equation — Équation (mathématiques) Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires). … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Transcendance mathématique

Nombre transcendant

Sommaire

Histoire

Quelques nombres transcendants connus

Problèmes ouverts

Esquisse de démonstration de la transcendance de $e$

Voir aussi

Références

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Transcendance mathématique

Nombre transcendant

Sommaire

Histoire

Quelques nombres transcendants connus

Problèmes ouverts

Esquisse de démonstration de la transcendance de e

Voir aussi

Références

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link

Esquisse de démonstration de la transcendance de $e$