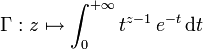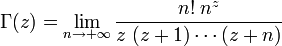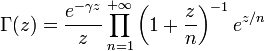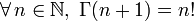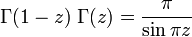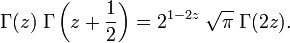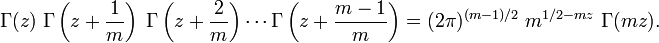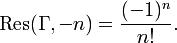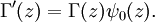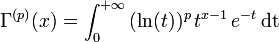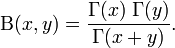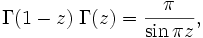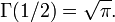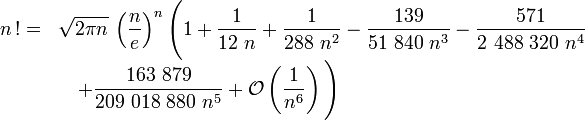- Fonction Gamma d'Euler
-
Fonction gamma
 Pour les articles homonymes, voir gamma (homonymie).
Pour les articles homonymes, voir gamma (homonymie).En mathématiques, la fonction gamma (ou fonction Gamma) est une fonction complexe, considérée également comme une fonction spéciale. Elle prolonge la fonction factorielle à l'ensemble des nombres complexes (excepté en certains points).
Sommaire
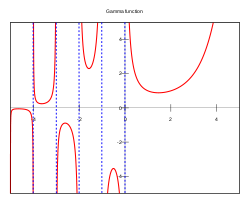
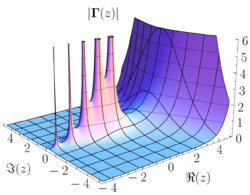
Définition
Pour
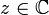 tel que
tel que 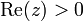 , on définit la fonction suivante, appelée fonction gamma, et notée par la lettre grecque Γ (gamma majuscule)
, on définit la fonction suivante, appelée fonction gamma, et notée par la lettre grecque Γ (gamma majuscule)Cette intégrale converge absolument sur le demi-plan complexe où la partie réelle est strictement positive.
En intégrant par parties, on montre que :
Cette fonction peut être prolongée analytiquement en une fonction méromorphe sur l'ensemble des nombres complexes, excepté pour z = 0, −1, −2, −3, ... qui sont des pôles. C'est ce prolongement qu'on appelle généralement "fonction gamma". Utilisant l'unicité du prolongement analytique, on montre que la fonction prolongée vérifie encore l'équation fonctionnelle précédente, ce qui permet une définition plus simple, à partir de l'intégrale et en calculant de proche en proche Γ pour z − 1, z − 2, etc.
Autres définitions
Les définitions suivantes de la fonction gamma par produits infinis, dues respectivement à Euler et Weierstrass, ont un sens pour les nombres complexes z qui ne sont pas des entiers négatifs ou nuls :
où γ est la constante d'Euler-Mascheroni.
Propriétés
Lien avec la factorielle
La fonction gamma vérifie l'identité :
Comme en particulier Γ(1) = 1, on en déduit :
La fonction gamma est donc généralement perçue comme un prolongement de la factorielle à l'ensemble des nombres complexes (excepté les entiers négatifs ou nuls).
Une notation alternative est la fonction pi, introduite par Gauss :
de telle façon que :
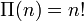 .
.
Caractérisations
sur l'ensemble des réels
La fonction gamma est entièrement caractérisée sur
 par les trois propriétés suivantes (théorème de Bohr-Mollerup):
par les trois propriétés suivantes (théorème de Bohr-Mollerup):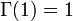
- la fonction composée
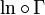 est convexe sur
est convexe sur 
- Pour tout
 , on a :
, on a : 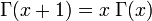
sur le demi-plan complexe Re(z)>0
La fonction gamma est entièrement caractérisée parmi les fonctions holomorphes du demi-plan complexe Re(z)>0 par les trois propriétés suivantes (théorème de Wielandt):
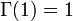
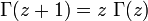
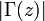 est bornée dans la bande
est bornée dans la bande 
Autres propriétés
La fonction gamma vérifie la formule de réflexion d'Euler, ou formule des compléments :
et la formule de duplication :
La formule de duplication est un cas particulier du théorème de multiplication :
Cette fonction apparaît également dans des formules incluant la fonction zêta de Riemann.
La fonction gamma possède un pôle d'ordre 1 en z = −n pour tout entier naturel n. Le résidu de la fonction en ce pôle est donné par :
La fonction gamma est indéfiniment dérivable sur
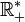 . Sa dérivée est exprimée à l'aide de la fonction polygamma :
. Sa dérivée est exprimée à l'aide de la fonction polygamma :Plus généralement, sa dérivée p-ième possède l'expression intégrale suivante:
Lien avec les sommes de Gauss
La définition de la fonction gamma sous forme d'intégrale la fait apparaître comme une convolution entre un caractère additif (l'exponentielle) et un caractère multiplicatif (
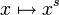 ).
).Lien avec d'autres fonctions
Dans la définition de la fonction gamma sous forme d'intégrale, les bornes de l'intégrale sont fixées ; la fonction gamma incomplète est la fonction obtenue en en modifiant la borne inférieure ou la borne supérieure.
La fonction gamma est reliée à la fonction bêta par la formule :
Le logarithme de la fonction gamma est parfois appelé lngamma. Il intervient notamment dans la résolution des problèmes de propagation d’ondes[1] : l'équation fonctionnelle de la fonction lngamma est :
- lnΓ(z) = lnΓ(z + 1) − ln(z).
Si l’on connaît les valeurs de la fonction sur une bande de largeur 1 en Re(z), on obtient par cette relation les valeurs dans une bande voisine de même largeur, et l’on peut répéter ce procédé. Partant d’un z avec Re(z) >> 1 pour lequel on connaît une bonne approximation, on peut ainsi atteindre la valeur pour un z quelconque.
Rocktaeschel (1922, suivant une indication de Gauss) propose[2] :
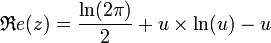 ,
,
avec
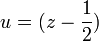 , comme approximation (très bonne malgré sa singularité en ½,0). Appliquant m fois le transfert, on obtient[3] :
, comme approximation (très bonne malgré sa singularité en ½,0). Appliquant m fois le transfert, on obtient[3] : 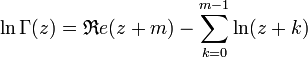
La dérivée du logarithme de la fonction gamma est appelée fonction digamma. Les dérivées d'ordre supérieur sont les fonctions polygamma.
Un analogue de la fonction gamma sur un corps fini ou un anneau fini est fourni par les sommes de Gauss.
L'inverse de la fonction gamma est une fonction entière.
Valeurs particulières
Cette section indique quelques valeurs particulières de la fonction gamma et de ses dérivées. La valeur de Γ(1 / 2) peut être déduite de la formule des compléments :
ce qui implique :
Cette valeur permet de déterminer les autres valeurs de la fonction gamma pour les demi-entiers.
-
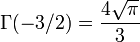
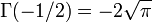
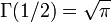
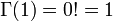
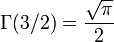
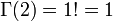
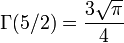
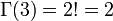
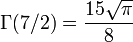

et dans le cas général : 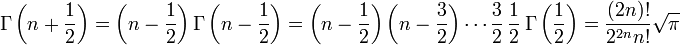
En ce qui concerne ses dérivées, avec γ la constante d'Euler-Mascheroni: 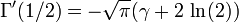
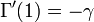

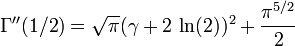
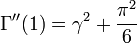
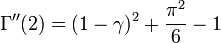
Formule asymptotique de Stirling
La formule de Stirling donne un équivalent de la fonction Gamma, et par conséquent de la factorielle, au voisinage de l'infini.
Pour la factorielle, elle s'écrit :
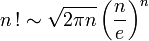 ,
,
ou, pour une meilleure précision :
Annexes
Bibliographie
- Jean Dieudonné, Calcul infinitésimal [détail des éditions], pp.292-296 (1968), éd. Hermann
- E. T. Witthaker, G. N. Watson, A course of modern analysis, Cambridge University Press, coll. « Cambridge Mathematrical Library », 1927 (4e éd.) (réimpr. 1996), 608 p. (ISBN 0-521-58807-3), « XII - The Gamma function », p. 235-364
Notes et références
- ↑ K. Rawer, Wave Propagation in the Ionosphere, Kluwer Academic Publishers, Dordrecht, 1993
- ↑ D'après O.R. Rocktäschel, Methoden zur Berechnung der Gammafunktion für komplexes Argument, Université de Dresde, Dresde, 1922, thèse de doctorat.
- ↑ P.E.Böhmer, Differenzengleichungen und bestimmte Integrale, Köhler Verlag, Leipzig, 1939.
Voir aussi
Articles connexes
- Constante de Gauss
- Distribution gamma
- Fonction bêta
- Fonction digamma
- Fonction gamma elliptique
- Fonction gamma incomplète
- Fonction gamma multivariable
- Fonction polygamma
- Fonction trigamma
- Formule de Chowla-Selberg
- Formule de Stirling
- Théorème de Bohr-Mollerup
- Fonctions spéciales
- Portail des mathématiques
Catégories : Fonction gamma ou associée | Fonction hypergéométrique | Fonctions spéciales
Wikimedia Foundation. 2010.