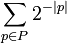Constante de Chaitin

Dans le sous-domaine de l’informatique qu’est la théorie algorithmique de l’information, une constante Oméga de Chaitin est un nombre réel, associé à un modèle de calcul ou à un langage de programmation donné, défini comme étant la probabilité qu’un programme informatique de ce modèle, généré aléatoirement, finira par s'arrêter. Il existe donc une infinité dénombrable de constantes de Chaitin, chacune associée à un modèle de calcul donné.

Ces nombres ont été définis et étudiés par Grégory Chaitin. Il est démontré qu'un Oméga est un nombre normal qui n'est pas calculable au sens de Turing : un algorithme donné ne permet de calculer qu'un nombre fini de ses décimales.

Les constantes Oméga sont d'une grande importance en théorie algorithmique de l'information car elles sont un exemple de nombre disposant d'une définition précise et univoque et qui est cependant fondamentalement non calculable.

Il est également possible de choisir arbitrairement un nombre fini de décimales comme de nouveaux axiomes : on sait alors caractériser le modèle de calcul (spécialement conçu) correspondant^[1].

Sommaire 1 Contexte 2 Définition de la probabilité d'arrêt 3 Interprétation comme probabilité 4 Représentation de l'expérience 5 Constante de Chaitin et théorie des nombres 6 Propriétés des nombres Ω 7 Notes et références 8 Voir aussi

Contexte

La définition d'une probabilité d'arrêt suppose qu'aucun programme ne résulte de l'extension d'un autre.

On considère une fonction F à deux arguments. F est dite universelle si pour toute fonction calculable f d'une seule variable x il y a une constante p telle que pour tout x, F(p,x) = f(x) ; en d'autres mots, F peut être utilisée pour simuler n'importe quelle fonction calculable d'une seule variable. p représente un "programme" pour f, et F représente un émulateur qui exécute ce programme ; pour chaque p, f(x) = F(p,x) est calculable.

Le domaine de F est l'ensemble de tous les programmes p tels que F(p,x) soit définie pour au moins une valeur de x. Selon la convention ci-dessus, il n'existe pas dans le domaine deux programmes différents p₁ et p₂ tels que l'un d'eux soit une extension de l'autre : on dit que F est sans préfixe.

Ceci revient à parler de la machine universelle (machine de Turing) correspondant à F dont les programmes ont une séquence de fin.

Définition de la probabilité d'arrêt

Soit 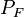le domaine d'une fonction universelle 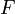répondant aux conditions ci-dessus. Alors :

,

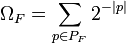où | p | est la longueur de p.

Bien qu'il y ait plusieurs probabilités d'arrêt dépendant du code utilisé pour générer les programmes, on a l'habitude d'utiliser la lettre Ω pour désigner cette probabilité, comme si elle était unique. Quand aucun code particulier n'est spécifié, on parle plutôt de construction de Chaitin.

Interprétation comme probabilité

On considère l'espace de Cantor formé de toutes les suites infinies de 0 et de 1. Une probabilité d'arrêt peut être interprétée comme la mesure d'un certain sous-ensemble de cet espace.

La mesure probabiliste dans cet espace est définie de façon à ce que pour toute chaîne x l'ensemble des suites qui commencent par x mesure 2^-|x|. Ceci entraîne que pour tout entier naturel n l'ensemble des suites f de l'espace de Cantor telles que f(n) = 1 mesure 0,5 et que l'ensemble des suites dont le n^ième élément est 0 mesure aussi 0,5.

Soit 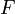une fonction universelle calculable sans préfixe telle que décrite plus haut. Le domain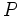e de 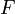est un ensemble infini de chaînes :

.

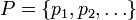Chaque 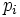détermine un sous-ensemble S_i de l'espace de Cantor, ce sous-ensemble contient toutes les suites qui commencent par 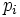. Les S_i étant disjoints - puisque par hypothèse aucun des 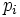n'est inclus dans un autre - la somme :

représente la mesure de .

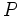De cette façon, Ω_F est la probabilité qu'une suite de l'espace de Cantor choisie au hasard commence par une chaîne qui soit un élément du domaine de 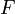. C'est pour cette raison que Ω_F s'appelle la "probabilité d'arrêt".

Représentation de l'expérience

La constante Ω est définie à partir de la probabilité d'arrêt d'un programme de la façon suivante : on effectue une série de tirages aléatoires (de 0 ou de 1 si on écrit en binaire) jusqu'à obtenir la séquence de fin correspondant à la machine universelle considérée ; on teste alors le programme obtenu. On considère qu'il y a échec quand on n'obtient jamais la séquence de fin dans les tirages aléatoires ou quand le programme ne s'arrête jamais.

Constante de Chaitin et théorie des nombres

La détermination d'une constante de Chaitin permettrait, en théorie, de résoudre certains problèmes en théorie des nombres, dont la conjecture de Goldbach et l' hypothèse de Riemann.^[2] La conjecture de Goldbach dit que tout nombre pair plus grand que 2 est la somme de deux nombres premiers. Il s'agirait, étant donné un nombre pair donné, de lancer une recherche par ordinateur pour trouver les deux nombres premiers correspondants. Si la conjecture de Goldbach est vraie, le programme incrémente au nombre pair suivant et poursuit la recherche. S'il n'y a pas de tels nombres premiers, le programme s'arrête, un contre-exemple a été trouvé et la conjecture de Goldbach a été réfutée. Si la longueur du programme p est de N bits, Oméga peut théoriquement être mise à contribution comme suit :

On exécute en parallèle tous les programmes longs de N+1 bits ou moins. Si p s'arrête, la conjecture de Goldbach est réfutée ; si par contre, il ne s'arrête pas alors que suffisamment d'autres programmes se sont arrêtés pour que la constante de Chaitin soit atteinte, alors il ne stoppera jamais et la conjecture de Goldbach est prouvée.

Cela suppose évidemment que l'expérimentateur ne soit pas limité en ressources et en temps, mais ce n'est pas l'objection principale. Ce qui se passe, c'est que la constante fonctionne en fait comme un oracle compressé, et qui contient une réponse au problème de l'arrêt pour toutes les machines de Turing ; on voit donc que cette constante est par essence non calculable...

Propriétés des nombres Ω

Les nombres Ω présentent maintes propriétés intéressantes et surprenantes.

• Un nombres Ω n'est pas calculable au sens de Turing : s'il l'était, on pourrait déterminer le problème de l'arrêt.
• Un nombre Ω est irrationnel, puisqu'il n'est pas calculable, et son développement binaire, décimal ou dans n'importe quelle base, est donc infini.
• Pour la même raison un nombre Ω est transcendant (il n'est pas solution d'une équation polynomiale à coefficients entiers).
• Le produit de deux nombres Ω est un autre nombre Ω (associé à une autre machine universelle), de même que la somme de deux nombres Ω si elle est strictement comprise entre 0 et 1, et toute suite extraite des décimales d'un nombre Ω (comme une décimale sur deux, ou celles de rang premier) est un autre nombre Ω.
• Un nombre Ω est un nombre normal et un nombre univers en toute base : dans toute base de numération, ses décimales sont équiréparties, et toute suite finie de chiffres se trouve quelque part dans son expression dans cette base (dans tout nombre Ω écrit en binaire, il y a par exemple une suite d'un milliard de 0 successifs)^[3].
• Pour une théorie axiomatique récursivement axiomatisable qui permet d'interpréter l'arithmétique, par exemple l'arithmétique de Peano ou la théorie des ensembles, et sous une hypothèse de cohérence plus forte que la cohérence simple^[4], il existe un rang à partir duquel, bien qu'un des énoncés "le bit suivant du développement binaire est 0" ou "le bit suivant du développement binaire est 1" (en binaire) soit vrai, il est impossible de démontrer lequel des deux l'est, c'est-à-dire qu'ils sont indécidables dans la théorie en question. Solovay a renforcé ce résultat, en modifiant astucieusement une fonction universelle de Chaitin, en fonction d'une théorie donnée (vérifiant les mêmes hypothèses), pour exhiber un nombre Ω, qui dépend donc de cette théorie, et dont il est impossible de décider un seul chiffre dans celle-ci.^[5]

Notes et références

Voir aussi

• Problème de l'arrêt
• Nombre définissable
• Complexité de Kolmogorov

• Portail de l’informatique
• Portail des mathématiques