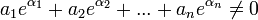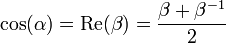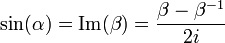Theoreme de Lindemann-Weierstrass

Article d'une série sur
la constante mathématique e
Logarithme naturel
Applications
Intérêts composés · Identité d'Euler et Formule d'Euler · Demi-vie et Croissance exponentielle/Décroissance exponentielle
Définitions
Démonstration de l'irrationalité de e · Représentations de e · Théorème de Lindemann-Weierstrass
Personnes
John Napier · Jacques Bernoulli · Leonhard Euler
Conjecture de Schanuel

En mathématiques, le théorème de Lindemann-Weierstrass établit que si 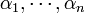sont des nombres algébriques qui sont linéairement indépendants sur les nombres rationnels, alors 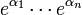sont algébriquement indépendants sur les nombres algébriques.

En d'autres termes, l'ensemble 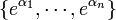possède le degré de transcendance n sur . Une formulation équivalente du théorème est la suivante : si 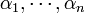sont des nombres algébriques distincts alors les sont linéairement indépendants sur les nombres algébriques, c’est-à-dire:

avec les a_i algébriques non tous nuls.

Le théorème fut nommé ainsi en l'honneur de Ferdinand von Lindemann, qui prouva le cas particulier de la transcendance de π, et Karl Weierstrass.

Transcendance de e et π

La transcendance de e et celle de pi sont des corollaires immédiats de ce théorème. Supposons que α soit un nombre algébrique différent de zéro ; alors {α} est un ensemble linéairement indépendant sur les nombres rationnels, et par conséquent {e^α} possède un degré de transcendance égal à un sur les nombres rationnels ; en d'autres termes e^α est transcendant.

En utilisant l'autre formulation, nous pouvons argumenter que si {0,α} est un ensemble de nombres algébriques distincts, alors l'ensemble {e⁰,e^α}} = {1,e^α}} est linéairement indépendant sur les nombres algébriques, et ainsi e^α est immédiatement vu comme étant transcendant. En particulier, e¹ = e est transcendant. Donc, si β = e^iα est transcendant, alors sa partie réelle et sa partie imaginaire :

et

le sont aussi. Car sinon on aura:

2cos(α)e^iα − e^2iα − 1 = 0

et

2isin(α)e^iα − e^2iα + 1 = 0

ce qui est absurde.

Par conséquent, si π était algébrique, cos(π) = − 1 et sin(π) = 0 seraient transcendants, ce qui prouve par l'absurde que π n'est pas algébrique, autrement dit qu'il est transcendant.

Conjecture p-adique

La conjecture p-adique de Lindemann-Weierstrass affirme que ce résultat est vrai pour les nombres p-adique : si 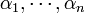sont un ensemble de nombres algébriques linéairement indépendants sur les nombres rationnels tels que | α_i | _p < 1 / p pour un certain nombre premier p, alors les exponentielles p-adiques sont transcendantes algébriquement indépendantes.

L'impossible quadrature du cercle

Lindemann montre que le problème de la quadrature du cercle se résume à la transcendance de la racine du nombre π. En prouvant que ce nombre n'est pas transcendant, il parvient à montrer qu'il est impossible de fabriquer un carré dont le centre gravité serait confondu avec l'origine d'un disque et qui aurait même aire que celui-ci, résolvant ainsi par la négative l'un des plus anciens problèmes de mathématiques depuis l'Antiquité.

• Portail des mathématiques