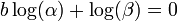Septieme probleme de Hilbert
- Septieme probleme de Hilbert
-
Septième problème de Hilbert
Le septième problème de Hilbert concerne l'irrationalité et la transcendance de certains nombres (Irrationalität und Transzendenz bestimmter Zahlen). Dans sa formulation géométrique, il demande quand l'assertion suivante est démontrable :
- Dans un triangle isocèle, si le rapport de l'angle de la base à l'angle du sommet est algébrique mais non rationnel, alors le rapport entre la base et le côté est toujours transcendant.
Un cas particulier de ce problème demande :
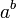 est-il un transcendant, pour
est-il un transcendant, pour 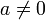 et
et 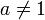 algébrique et b algébrique irrationnel ?
algébrique et b algébrique irrationnel ?
Lorsque b est rationnel, 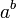 sera algébrique.
sera algébrique.
Le problème particulier fut résolu par Aleksandr Gelfond en 1934, et raffiné par Theodor Schneider en 1935. Ils ont démontré que 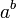 est transcendant lorsque b est algébrique et irrationnel. Ce résultat est connu sous le nom de théorème de Gelfond ou de Gelfond-Schneider.
est transcendant lorsque b est algébrique et irrationnel. Ce résultat est connu sous le nom de théorème de Gelfond ou de Gelfond-Schneider.
À partir du point de vue des généralisations, ceci est le cas
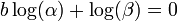
de la forme linéaire générale en logarithmes.
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégories : Théorie des nombres | Problème de Hilbert
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Septieme probleme de Hilbert de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Septième problème de hilbert — Le septième problème de Hilbert concerne l irrationalité et la transcendance de certains nombres (Irrationalität und Transzendenz bestimmter Zahlen). Dans sa formulation géométrique, il demande quand l assertion suivante est démontrable :… … Wikipédia en Français
Septième problème de Hilbert — Le septième problème de Hilbert concerne l irrationalité et la transcendance de certains nombres (Irrationalität und Transzendenz bestimmter Zahlen). Il pose deux questions, dont la première est énoncée géométriquement mais peut se reformuler… … Wikipédia en Français
Dixième problème de Hilbert — Le dixième problème de Hilbert demande de trouver une méthode algorithmique générale pour la recherche des solutions entières des équations diophantiennes à plusieurs inconnues, c est à dire des équations polynômiales à coefficients entiers. Il… … Wikipédia en Français
Troisieme probleme de Hilbert — Troisième problème de Hilbert Le troisième problème de Hilbert est l un des 23 problèmes de Hilbert. Considéré comme le plus facile, il traite de la géométrie des polyèdres. Étant donnés deux polyèdres d égal volume, est il possible de découper… … Wikipédia en Français
Troisième problème de Hilbert — Le troisième problème de Hilbert est l un des 23 problèmes de Hilbert. Considéré comme le plus facile, il traite de la géométrie des polyèdres. Étant donnés deux polyèdres d égal volume, est il possible de découper le premier polyèdre en des… … Wikipédia en Français
Troisième problème de hilbert — Le troisième problème de Hilbert est l un des 23 problèmes de Hilbert. Considéré comme le plus facile, il traite de la géométrie des polyèdres. Étant donnés deux polyèdres d égal volume, est il possible de découper le premier polyèdre en des… … Wikipédia en Français
Neuvieme probleme de Hilbert — Neuvième problème de Hilbert Le neuvième problème de Hilbert est l un des vingt trois problèmes ouverts proposés comme défis du XXe siècle par David Hilbert au second congrès international de mathématiques en 1900. Il consiste à généraliser… … Wikipédia en Français
Neuvième Problème De Hilbert — Le neuvième problème de Hilbert est l un des vingt trois problèmes ouverts proposés comme défis du XXe siècle par David Hilbert au second congrès international de mathématiques en 1900. Il consiste à généraliser la loi de réciprocité… … Wikipédia en Français
Neuvième problème de hilbert — Le neuvième problème de Hilbert est l un des vingt trois problèmes ouverts proposés comme défis du XXe siècle par David Hilbert au second congrès international de mathématiques en 1900. Il consiste à généraliser la loi de réciprocité… … Wikipédia en Français
Seizième problème de Hilbert — Le seizième problème de Hilbert est l un des 23 problèmes de Hilbert. Il comporte deux parties. La première concerne le nombre de branches réelles (ovales) d une courbe algébrique, et leur disposition ; de nombreux résultats modernes… … Wikipédia en Français
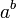 est-il un transcendant, pour
est-il un transcendant, pour 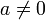 et
et 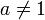 algébrique et b algébrique irrationnel ?
algébrique et b algébrique irrationnel ?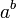 sera algébrique.
sera algébrique.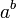 est transcendant lorsque b est algébrique et irrationnel. Ce résultat est connu sous le nom de théorème de Gelfond ou de Gelfond-Schneider.
est transcendant lorsque b est algébrique et irrationnel. Ce résultat est connu sous le nom de théorème de Gelfond ou de Gelfond-Schneider.