Théorème de Cauchy-Lipschitz

Pour les articles homonymes, voir Cauchy.

Cauchy développe une première version du théorème de l'article.

En mathématiques, et plus précisément en analyse, le théorème dit de Cauchy-Lipschitz, (ou de Picard–Lindelöf chez les anglophones) concerne les équations différentielles. Sous des conditions de régularité^{[Note 1]} d'une fonction définissant une équation, il garantit l'unicité d'une solution répondant à une condition initiale dite de Cauchy et l'existence d'une solution maximale.

Selon les auteurs, ce théorème s'exprime de manière plus ou moins forte. Sous une forme plus élaborée, ce théorème assure que la solution varie continûment si la condition initiale est modifiée, et il en est de même si la fonction définissant l'équation dépend continûment d'un paramètre. Si l'équation est définie par une fonction de classe C^p, la solution est de classe C^{p+1[Note 2]}. Ce théorème peut encore être généralisé au cas où l'équation différentielle n'est plus à valeurs dans un espace vectoriel, mais dans une variété différentielle^{[Note 3]}.

Certaines lois physiques, comme le principe fondamental de la dynamique, se traduisent par des équations différentielles vérifiant les hypothèses du théorème. Il assure alors le caractère déterministe du mécanisme décrit par la loi. Ce déterminisme ne se traduit pas toujours par une possibilité de prédiction, la théorie du chaos montre l'existence de possibles phénomènes fortuits^{[Note 4]}.

Une première version est démontrée par Augustin-Louis Cauchy durant la première moitié du XIX^e siècle, à l'aide d'une technique d'approximation découverte par Leonhard Euler au siècle précédent. Rudolf Lipschitz généralise l'énoncé en élargissant un peu la classe des équations qui s'y rapportent. Le théorème n'en reste pas moins uniquement un résultat d'existence locale. C'est à la fin de ce siècle que les techniques de démonstration, ainsi que l'énoncé du théorème, sont profondément modifiés. À la suite des travaux de Lazarus Fuchs, les mathématiciens Émile Picard, Paul Painlevé et Henri Poincaré développent une version moderne de l'analyse des équations différentielles. Cette vision permet d'apporter des éléments de réponse sur les solutions maximales, l'unicité et la régularité de la solution. Une version relativement moderne est publiée en 1894 par Ernst Lindelöf. Le théorème se démontre maintenant généralement à l'aide d'un théorème du point fixe et d'une approche topologique, classique en analyse fonctionnelle.

Préambule

Énoncés

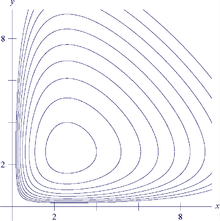
Les graphes des fonctions d'évolution des populations pour les équations de Lotka-Volterra forment une partition de R₊².

Dans tout le reste de l'article, E désigne un espace de Banach, Ω un ouvert de RxE et f une fonction continue de Ω dans E. L'objectif est d'étudier l'équation différentielle du premier ordre suivante :

Avec la condition de Cauchy C : x(t₀) = x₀, où le couple (t₀, x₀) est un élément de Ω.

Il existe plusieurs manières d'exprimer le théorème de Cauchy-Lipschitz, dont la forme suivante :

• Si la fonction f est localement lipschitzienne par rapport à la deuxième variable, il existe une et une seule solution maximale à l'équation (1) respectant la condition de Cauchy C. Son intervalle de définition est ouvert^[1].

Ce théorème dispose des corollaires suivants^[2] :

• Sous les mêmes conditions que le théorème, si σ est une solution de l'équation différentielle (1) respectant la condition C et définie sur un intervalle, cet intervalle est inclus dans celui de la solution maximale et la restriction de la solution maximale à cet intervalle est confondue avec σ.
• Les graphes des solutions maximales forment une partition de Ω.
• Si f est une fonction de classe C^p, les solutions sont de classe C^p+1.

L'expression théorème de Cauchy-Lipschitz est aussi utilisée pour désigner d'autres résultats plus évolués. Il est possible de considérer non pas seulement la fonction solution s mais aussi la fonction qui au couple (x, t) associe l'image de t par la solution égale à x à un instant initial t₀. On obtient une fonction appelée flot. Si la fonction f est de classe C^p, le flot l'est aussi. Il est aussi possible d'étudier la régularité des solutions si la fonction f dépend d'un paramètre. Ces résultats sont esquissés dans le paragraphe Généralisations et traités plus en profondeur dans l'article Flot (mathématiques).

D'autres résultats, qui ne portent pas le nom de théorème de Cauchy-Lipschitz sont présentés dans le paragraphe : Généralisations.

Déterminisme et chaos

Henri Poincaré montre que le caractère déterministe d'une équation différentielle vérifiant le théorème de Cauchy-Lipschitz n'empêche pas l'impossibilité de certaines prédictions.

Pour le mathématicien Vladimir Arnold « Les équations différentielles sont le pivot de la conception scientifique du monde »^[3]. En physique, les équations différentielles vérifient de manière très générale les hypothèses du théorème de l'article^{[Note 5]}, il en est ainsi de celle qui régit la loi de la gravitation universelle ou l'interaction électromagnétique. Ces équations sont intrinsèquement déterministes et c'est l'une des conséquences du théorème de l'article^[4]. Ce déterminisme, c'est-à-dire la capacité de la physique à prévoir, par exemple la trajectoire des planètes, était connu bien avant le théorème. La célèbre citation de Voltaire l'atteste « En apercevant l’ordre, l'artifice prodigieux, les lois mécaniques et géométriques qui règnent dans l’univers, ... je suis saisi d’admiration et de respect. »^[5]. Il en déduisait « le chaos est précisément à l'opposé de toutes les lois de la nature. »^[5]. Curieusement, les analyses fines de la fin du XIX^e siècle démontrent à la fois la pertinence du caractère déterministe de ces lois physiques et réduisent cette idée de Voltaire à l'état de chimère.

Les travaux mathématiques de cette époque montrent effectivement qu'une trajectoire, suivant une loi physique de cette nature, est unique et parfaitement déterminée^{[Note 6]}. En revanche, les études de Poincaré sur la stabilité du système solaire mettent en évidence la faute de raisonnement. Ce mathématicien précise : « Une cause très petite, qui nous échappe, détermine un effet considérable que nous ne pouvons pas ne pas voir, et alors nous disons que cet effet est dû au hasard. Si nous connaissions exactement les lois de la nature et la situation de l'univers à l'instant initial, nous pourrions prédire exactement la situation de ce même univers à un instant ultérieur. Mais, lors même que les lois naturelles n'auraient plus de secret pour nous, nous ne pourrions connaître la situation qu'approximativement. Si cela nous permet de prévoir la situation ultérieure avec la même approximation, c'est tout ce qu'il nous faut, nous disons que le phénomène a été prévu, qu'il est régi par des lois ; mais il n'en est pas toujours ainsi, il peut arriver que de petites différences dans les conditions initiales en engendrent de très grandes dans les phénomènes finals ; une petite erreur sur les premières produirait une erreur énorme sur les derniers. La prédiction devient impossible et nous avons le phénomène fortuit. »^[6]

Le théorème de Cauchy-Lipschitz indique bien qu'une prévision parfaite est possible, mais uniquement sous réserve de connaître parfaitement la condition initiale. Certains systèmes dynamiques sont rapidement imprévisibles pour la raison qu'indique Poincaré. On utilise maintenant le terme de chaos pour décrire cette situation. Il ne se produit pas systématiquement, le théorème de Poincaré-Bendixson précise un contexte où il ne peut avoir lieu, mais les hypothèses sont restrictives et le résultat peu généralisable^{[Note 7]}.

Vocabulaire

Plusieurs termes ne sont pas nécessairement intuitifs, ce paragraphe en propose les définitions^{[Note 8]}.

Vocabulaire générique aux équations différentielles

Une partie du vocabulaire utilisée pour exprimer le théorème est générique aux équations différentielles ou fonctionnelles. Le terme espace de Banach désigne un espace vectoriel normé et complet, c'est-à-dire que pour la métrique associée à la norme, toute suite de Cauchy converge. Un exemple simple est un espace vectoriel réel normé de dimension finie. Pour une compréhension plus facile, le lecteur peut imaginer que E désigne l'ensemble des nombres réels. Dans l'article, tous les espaces de Banach considérés sont des espaces réels.

Une solution de l'équation est parfois désignée à l'aide de l'expression suivante, que l'on trouve fréquemment dans la littérature traitant du sujet de l'article :

• Une courbe intégrale^[7] de l'équation (1) est une fonction d'un intervalle de R dans E dont le graphe est inclus dans Ω, et qui est solution de l'équation (1).

D'une équation différentielle d'ordre n (n > 1) à une équation d'ordre 1

L'équation (1) est dite du premier ordre^[8]. Dans le cas général, une équation différentielle d'ordre n est du type^[9], si g désigne une fonction définie sur un ouvert de RxEⁿ :

Il peut sembler étonnant de restreindre le théorème uniquement aux équations du premier ordre. En fait, le théorème se généralise aisément à une équation d'ordre n. L'équation (2) peut se lire^[10] aussi comme une équation du premier ordre à valeur dans Eⁿ de variable y(t) = (x₁(t),...,x_n(t)). L'équation (2) s'écrit encore :

La solution x(t) est alors la première coordonnée de la solution y(t), la k^ième coordonnée de y(t) correspond à la dérivée (k - 1)^ième de la fonction x(t), où k est un entier variant entre 1 et n.

Équation différentielle autonome du premier ordre

Il existe un cas particulier, celui où la fonction f est définie sur un ouvert de E et non pas sur un ouvert de RxE. L'équation (1) s'écrit alors

Ω désigne un ouvert de E et l'équation est dite autonome. Ce cas particulier est étudié pour les démonstrations.

Vocabulaire spécifique

D'autres termes sont plus spécifiquement utilisés dans le contexte du théorème de l'article. L'équation différentielle (1) possède généralement plusieurs solutions. Pour cette raison, on ajoute parfois une condition particulière :

• Une condition de Cauchy C est un couple (t₀, x₀) élément de Ω. Une fonction s définie sur un intervalle de R et à valeurs dans E solution de l'équation (1) vérifie la condition de Cauchy C si, et seulement si, l'intervalle de définition de s contient t₀ et s(t₀) = x₀.

Résoudre le problème de Cauchy^[11] consiste à trouver une solution de l'équation (1) vérifiant la condition de Cauchy C. Cette définition est un peu intuitive. Si l'équation différentielle modélise un courant parcourant une étendue d'eau, c'est-à-dire qu'à l'instant t et au point x le courant est égal à f(t,p), il est possible de poser dans l'eau un bouchon à l'instant t₀ au point x₀, la trajectoire du bouchon est la solution de l'équation. Il existe bien une solution pour chaque couple (t₀, x₀) (qui peuvent d'ailleurs être confondues).

Une condition de Cauchy ne suffit pas à rendre la solution unique. Considérons l'ensemble S des solutions de l'équation (1) vérifiant la condition de Cauchy C et définies sur un intervalle. Cet ensemble est muni d'une relation d'ordre. Une solution s₁ de S est plus petite qu'une solution s₂ de S lorsque le domaine de définition de s₁ est inclus dans celui de s₂.

• Une courbe intégrale de S, satisfaisant la condition de Cauchy C, est dite maximale si, et seulement si, elle est définie sur un intervalle et qu'elle est maximale pour la relation d'ordre définie dans ce paragraphe.

Remarque : À la place de l'expression condition de Cauchy, on parle parfois de condition initiale^[7]. Les deux expressions sont synonymes.

Le théorème de Cauchy-Peano-Arzelà montre que l'unicité de la solution maximale vérifiant une condition de Cauchy donnée n'est généralement pas garantie. Pour que les hypothèses du théorème soient vérifiées, la fonction f doit aussi posséder une propriété de régularité. Si P(Ω) est la projection canonique sur E de Ω :

• La fonction f est dite localement lipschitzienne par rapport à la deuxième variable si, et seulement si, pour tout x de P(Ω), il existe un réel k strictement positif et un voisinage V de x dans P(Ω) tel que :

Exemples et usages

Champ constant

Dans cet exemple^[12] E est égal à R² le plan réel. L'équation différentielle est autonome, elle s'écrit x' = f(x) où f est la fonction constante de valeur le vecteur v de coordonnées (1, 0). Le domaine Ω de la fonction f est l'ensemble des points de R² est composé des points dont chaque coordonnée est, en valeur absolue, strictement plus petite que 3. Ce domaine est représenté par le carré bleu de la figure de droite. Une méthode de représentation de la fonction f consiste à dessiner les vecteurs f(x), où x est un point du domaine, en plaçant leurs origines au point x.

On recherche les solutions vérifiant la condition de Cauchy (0, x₀), ici les coordonnées de x₀ sont (-2, 2). Une solution s est de la forme :

La solution ne peut quitter le domaine Ω, en conséquence, la variable t prend nécessairement ses valeurs dans ]-1, 5[. La fonction f est bien continue et k-lipschitzienne en x, avec dans ce cas particulier k = 0. Le théorème de Cauchy-Lipschitz garantit qu'il n'existe qu'une unique courbe intégrale vérifiant une condition de Cauchy précise, comme ici celle donnée par le couple (0, x₀). Le graphe de cette solution est représentée en vert sur la figure.

Équation linéaire à coefficients constants

On considère encore une équation autonome, dont le domaine est cette fois R tout entier :

Une première difficulté apparaît. Le théorème de Cauchy-Lipschitz ne traite que des équations du premier ordre, c'est-à-dire ne faisant intervenir que la dérivée première et pas la dérivée seconde. En modifiant l'ensemble d'arrivée, il devient possible de transformer cette équation en équation du premier ordre. On considère maintenant l'endomorphisme f de R², qui à la base canonique (e₁, e₂) associe (e₂, e₁). Si v désigne la variable de la nouvelle équation différentielle, elle désigne une fonction de R dans R² et l'équation s'écrit :

Si l'on note (x(t), y(t)) la fonction variable v(t) la nouvelle équation différentielle s'écrit :

Autrement dit, la dérivée de la fonction x est égale à y et la dérivée de y est égal à x, ce qui signifie que la dérivée seconde de x est égal à x. La nouvelle équation est bien équivalente à l'ancienne. Sous cette nouvelle forme il est possible d'appliquer directement le théorème de l'article. Il indique que la condition de Cauchy s'exprime sous la forme de la valeur de x et de y (autrement dit la dérivée de x) en un point particulier. Le théorème de Cauchy indique qu'il existe une unique solution maximale à l'équation, si l'on fixe une valeur de la fonction x ainsi que sa dérivée. Par exemple, si l'on choisit x(0) = 0 et x' (0) = 2, on trouve l'unique courbe intégrale maximale s définie sur R par :

Étude d'une courbe intégrale

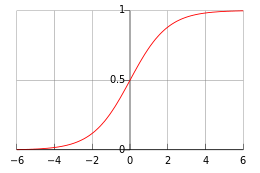
Graphe de la fonction logistique

Le théorème de Cauchy-Lipschitz peut être vu comme un outil permettant l'étude d'une courbe intégrale. Illustrons le par l'exemple d'une fonction logistique, définie par l'équation différentielle suivante :

L'équation s'écrit aussi x' = f(x) avec f(x) = x(1 - x). Soit s la solution maximale. La fonction f est une fonction polynomiale de degré 2 (parabole) de zéros 0 et 1 et positive entre ses racines. Le théorème de l'article s'applique car f est dérivable donc localement lipschitzienne. On suppose que l'image par la fonction s n'est pas incluse dans l'intervalle ]0, 1[. Toute fonction ayant pour image 1/2 et dépassant 1, passe nécessairement par la valeur 1, d'après le théorème des valeurs intermédiaires. Si une telle fonction était une solution, le point 1 contiendrait deux courbes intégrales : celle-là et la fonction constante égale à 1. L'unicité de la solution serait contredite. On peut appliquer le même raisonnement en 0. Le fait que s(t) prenne ses valeurs entre 0 et 1 montre que sa dérivée est strictement positive, la solution s(t) est strictement croissante.

Son domaine de définition est égale à R. En effet, la fonction s est uniformément continue car sa dérivée est bornée, elle peut être prolongée par continuité à l'adhérence de son domaine de définition. Cette prolongation est aussi une solution de l'équation, donc le domaine de définition est un fermé. Le théorème de l'article nous apprend qu'il contient la valeur 0 et qu'il est ouvert. Comme R est connexe et que le seul ouvert fermé non vide d'un connexe est l'ensemble entier, le domaine de définition est égal à R

La fonction s est strictement croissante est bornée, elle admet une limite en plus l'infini, et donc sa dérivée aussi. La seule valeur limite possible de la dérivée est 0, ce qui montre que la seule limite possible de s(t) est 1. Le même raisonnement montre que la limite en moins l'infini est 0. Enfin, on remarque que la fonction qui à t associe 1 - s(-t) est une solution vérifiant la condition de Cauchy x(0) = 1/2. Le théorème de l'article permet d'en déduire que les deux fonctions sont égales, ce qui signifie que la fonction s(t) - 1/2 est impaire et que la valeur 0 est l'abscisse de l'unique point d'inflexion de la courbe. L'équation montre que la dérivée en 0 est égale à 1/4, ce qui permet d'établir son graphe, représenté à droite.

Dans le cas de l'exemple choisi, on peut résoudre l'équation différentielle^{[Note 9]} et utiliser les méthodes classiques pour l'étude de la courbe intégrale, mais ce n'est pas toujours possible. Une équation différentielle n'a pas nécessairement des solutions s'exprimant sous la forme d'une expression algébrique construite à l'aide des fonctions élémentaires.

Théorème de Poincaré-Bendixson

Dans le plan, une équation différentielle autonome du premier ordre converge vers un point ou un cycle limite, à l'image de l'exemple illustré ici.

L'usage du théorème de l'article ne se limite pas à la résolution pratique des équations. Il sert aussi d'outil théorique, par exemple pour mieux comprendre le comportement quantitatif d'une équation différentielle. On peut considérer le cas d'une équation différentielle autonome dans R² ayant une solution p périodique. La courbe intégrale est un lacet simple, c'est-à-dire que son graphe forme une boucle sans point double. Soit maintenant une condition de Cauchy C correspondant à un point à l'intérieur de la boucle. Le théorème de l'article indique que la courbe intégrale maximale s vérifiant C ne pourra jamais traverser la boucle, si la fonction f définissant l'équation est localement lipschitzienne. La courbe s est donc bornée et si l'on suppose que le domaine de f contient l'intérieur de la boucle, la courbe s ne s'approche jamais trop du bord du domaine. Ceci suffit à démontrer que le domaine de définition de s est R tout entier.

Le théorème de Poincaré-Bendixson permet d'aller plus loin. Il indique que la courbe s est, soit convergente, soit sont comportement s'approche de plus en plus d'une fonction périodique. Cette configuration interdit la théorie du chaos^[13].

L'usage fait ici du théorème permet de comprendre qualitativement le comportement d'une courbe intégrale. Pour l'étude d'équation différentielle plus complexe, par exemple certains systèmes dynamiques, cette approche est indispensable. Il n'est en effet plus toujours possible de résoudre explicitement l'équation, ni même d'approximer la solution sur des longues périodes de temps.

Fragments d'histoire

Origines

Après avoir étudié de nombreux cas particuliers, Euler étudie sous sa forme générale, l'équation différentielle du premier ordre.

L'origine de la question traitée par le théorème est ancienne, elle porte initialement le nom de « problème inverse des tangentes »^[14]. À chaque point de l'espace, une droite est associée, le problème à résoudre est de trouver la courbe ayant, comme tangente en chaque point, une de ces droites, ce qui correspond en terme moderne à une équation différentielle autonome, de la forme x' = f(x). Kepler est un initiateur de cette question dans une étude sur la contenance d'un tonneau de vin en 1615^[15]. Si cette question est abordée par des mathématiciens comme Descartes, Fermat ou Roberval, qui développent cette approche dans des cas particuliers durant le XVII^e siècle, le progrès essentiel est l'œuvre de Newton et Leibnitz avec la découverte du calcul infinitésimal^[16]. Newton cherche surtout à obtenir un résultat à l'aide d'une série, Leibnitz recherche aussi des solutions exactes, sous forme de primitives de fonctions connues^[17].

Le siècle suivant est l'objet d'une systématisation de l'étude. Dans un premier temps « Des trésors d'ingéniosité ont été dépensés pour ramener à des quadratures d'innombrables équations différentielles particulières et comme l'écrit Paul Painlevé : la vague s'arrêta quand tout ce qui était intégrable, dans les problèmes naturels fût intégré. »^[17]. Euler, en 1768 étudie la manière d'approximer une solution^[18]. Il étudie le cas particulier x'(t) = f(t) et cherche une solution sur un intervalle [a, b]. Pour se faire, il partitionne l'intervalle à l'aide d'une suite a₀ = a, a₁, ..., a_n = b et, si c est élément de l'intervalle [a_i, a_i+1] il propose l'approximation suivante :

Dans le cas plus général de l'équation x'(t) = f(t, x(t)), il utilise la même méthode, qui donne :

Euler ne se pose pas la question de la convergence si le découpage est de plus en plus fin.

Les apports de Cauchy et de Lipschitz

Rudolf Lipschitz généralise le résultat de Cauchy.

Augustin Louis Cauchy (1789 - 1857) établit les premiers résultats généraux. Dans un premier temps, il précise sa méthode « Dans mes leçons données à l'École Polytechnique, comme dans la plupart des ouvrages ou mémoires que j'ai publié sur le calcul intégral, j'ai cru devoir renverser cet ordre et placer en premier lieu la recherche, non pas des intégrales générales, mais des particulières; en sorte que la détermination des constantes ou des fonctions arbitraires [pour l'équation aux dérivées partielles] ne fût plus séparée de la recherche des intégrales. »^[19]. Ce que Cauchy décrit ici est la démarche formalisée par le problème de Cauchy.

À l'aide de la formalisation de la notion de limite par Bolzano, son approche lui permet d'aller plus loin. La question x' = f(x) sur l'intervalle [a, b], si on lui ajoute la condition de Cauchy x(a) = x₀, change de nature. Ce n'est plus la recherche d'une primitive de f, mais le calcul d'une intégrale. Il montre que, avec les notations du paragraphe précédent, si a_i+1 - a_i tend vers 0 et que f est continue, la limite converge. Cette démarche est appliquée à l'équation x'(t) = f(t, x(t)) dans le cas où f, ainsi que sa différentielle, sont continues et bornées, avec les mêmes conditions, on obtient encore une convergence. C'est la première version du théorème de l'article^[20]. En 1835, sa méthode est généralisée aux fonctions holomorphes^[21].

Rudolf Lipschitz (1832 - 1903) reprend la même direction que son prédécesseur Cauchy, sans manifestement connaître la teneur de ses travaux. Il ne suppose plus que f possède une différentielle continue et bornée mais uniquement qu'elle vérifie la condition qui porte maintenant son nom^[22]. Cauchy utilise dans sa démonstration originale cette même propriété, mais la déduit à l'aide de l'une de ses découvertes, qu'il affectionne particulièrement : le théorème des accroissements finis^{[23],[Note 10]}.

Le formalisme moderne

La fin du XIX^e siècle voit une profonde mutation du théorème, tant dans la manière de le démontrer que dans l'enrichissement de son contenu, nécessaire pour mieux comprendre l'équation différentielle.

À la suite des travaux de Fuchs^[24], les objectifs deviennent plus ambitieux. Paul Painlevé et Emile Picard s'intéressent au cas général des équations différentielles de premier et second ordre et donc à leurs singularités^[25],[26]. Les objectifs d'Henri Poincaré sont encore plus généraux, à la suite d'une étude sur la stabilité du système solaire, il cherche à établir une théorie générale qui prendra le nom de système dynamique. Devant l'impossibilité d'établir des solutions explicites, Poincaré fonde les bases d'une théorie qualitative^[27]. Les objectifs sont, dans un premier temps l'étude des singularités, puis le comportement asymptotique (c'est-à-dire l'étude du comportement une fois le système stabilisé) et la sensibilité à la condition initiale.

Pour atteindre ces nouveaux objectifs, la formulation par Cauchy ou Lipschitz du théorème devient insuffisante. On cherche maintenant des éléments de réponse globaux sur les courbes intégrales et non plus uniquement un résultat local. Les questions sur la régularité de la solution deviennent essentielles. Enfin, on cherche à déterminer la nature de la modification de la courbe intégrale en fonction d'une modification de la condition initiale ou d'un paramètre de l'équation^[28]. Les méthodes pour y arriver diffèrent radicalement de l'approche de Cauchy qui étudiaient le comportement limite de la fonction polygonale imaginée par Euler. Elles se rapprochent de l'analyse fonctionnelle, le contexte de l'étude est maintenant un espace de fonctions disposant de propriétés géométriques. Le théorème à la source de la démonstration est celui du point fixe, sa forme initiale est l'œuvre de Picard^[29], ce théorème est maintenant vu comme une propriété générale d'espaces vectoriels particuliers, formalisés par Stefan Banach. Son application au théorème de l'article est l'œuvre du mathématicien finlandais Ernst Lindelöf^[30] en 1894. Pour cette raison, le théorème nommé en France d'après Cauchy et Lipschitz prend le nom, en langue anglaise de Picard–Lindelöf theorem^[31].

Généralisations

Il existe de nombreuses généralisations du théorème de Cauchy-Lipschitz. Les techniques utilisées pour sa démonstration permettent d'aller plus loin dans l'analyse des solutions d'une équation différentielle. Une rapide analyse montre qu'une solution est continument dérivable, mais rien n'indique ce qui se produit si la fonction f est plus régulière. On démontre^[32] que si f est de classe C^p, les solutions maximales le sont aussi. La branche des mathématiques étudiant un système dynamique se pose deux questions essentielles : quel est le comportement d'une courbe intégrale si t s'approche des bornes du domaine de définition ? Et quelle est la sensibilité à la condition initiale ? c'est-à-dire que se passe-t-il si x₀ subit une petite modification.

Enfin, l'article suppose que l'ensemble E est un espace de Banach, ce qui n'est pas l'unique cas étudié. Dans certaines situations, il est utile de considérer E comme une variété différentielle. Les théorèmes se transposent aisément dans ce nouvel univers^[33].

Flot

Pour l'étude de la sensibilité initiale, on étudie le flot qui permet d'énoncer une version plus forte du théorème de l'article.

L'un des objectifs de l'étude des systèmes dynamiques est celle de la sensibilité à la condition de Cauchy. Le vocabulaire et la représentation géométrique sont un peu différents de ce qui a été utilisé jusqu'à présent. Pour en comprendre l'origine, le plus simple est d'imaginer que Ω est un plan d'eau et que R représente le temps. Le plan d'eau est agité par un courant, représenté par la fonction f, appelé champ de vecteurs. En dimension 2, on représente ce champ de vecteurs en associant à certains points x de E une représentation graphique du vecteur f(x) (si le champ de vecteurs ne dépend pas du temps t), à l'image de la figure de droite. Une courbe intégrale satisfaisant à la condition de Cauchy C peut s'imaginer comme la trajectoire d'un bouchon placé dans l'eau à l'instant t₀ à la position x₀. Pour connaître d'un seul coup toutes les solutions de l'équation différentielle, il suffit de connaître le mouvement de la surface de l'eau, appelé flot, coulée ou encore courant^[34].

Avec ce concept, le théorème de l'article prend une nouvelle forme :

• Si f est continue et localement lipschitzienne par rapport à la deuxième variable, le flot est continu, dérivable par rapport à la première variable et localement lipschitzien par rapport à la deuxième.

Il est possible d'aller plus loin si f est plus régulière.

• Si f est de classe C^p, le flot l'est aussi.

Cette forme du théorème est plus forte que la précédente. Elle montre la régularité des solutions sous l'action d'une petite modification de la condition de Cauchy. Cet énoncé garantit l'absence d'une certaine forme de chaos. Les bifurcations sont impossibles et, sous réserve que t ne grandisse pas trop, les trajectoires restent proches si la condition de Cauchy est peu modifiée. Néanmoins, si le champ de vecteurs évolue avec le temps ou si E est de dimension strictement supérieure à deux, une autre forme de chaos peut s'installer.

Les formes précises des théorèmes et les démonstrations sont données dans l'article détaillé.

Théorème de Cauchy-Peano-Arzelà

Une bille roulant sur un demi-cylindre.

À la fin du XIX^e siècle, Giuseppe Peano, un mathématicien italien, s'interroge sur la pertinence des hypothèses du théorème de Cauchy-Lipschitz^[35] : que se passe-t-il si la fonction f, définissant l'équation (1), reste continue mais n'est pas localement-lipschitzienne par rapport à la deuxième variable ?

Une situation physique correspondant à ce cas est une bille roulant sans frottement sur l'arête d'un toit en V inversé aux branches de pente constante. Notons x la coordonnée transversale (perpendiculairement à l'arête) et y la coordonnée longitudinale (parallèlement à l'arête). En appliquant les lois de la mécanique, on obtient une équation différentielle autonome du premier ordre dans R², si on ne considère que les solutions qui penchent vers les valeurs positives de x :

Si t₀ désigne un réel positif, toutes les solutions suivantes vérifient l'équation précédente, pour la même condition de Cauchy, à savoir que le solide est à l'instant 0, à la position (0,0) :

D'autres exemples sont donnés dans l'article détaillé.

Ici, on remarque que si l'unicité n'est plus valable, l'existence reste vraie. De manière plus générale, si la fonction f de l'équation (1) est continue et bornée et si E est de dimension finie, l'existence d'une solution est garantie. Ce résultat est appelé théorème de Cauchy-Peano-Arzelà.

Extension aux équations aux dérivées partielles

La généralisation du théorème pour les équations aux dérivées partielles suppose des hypothèses plus fortes pour un résultat plus faible. La fonction f définissant l'équation doit être analytique ainsi que les conditions aux limites qui remplacent celle de Cauchy. Aucune information n'est fournie dans le cas d'une modification des conditions aux limites ou d'un paramètre. Ce théorème est appelé : théorème de Cauchy-Kowalevski.

Démonstrations

Préambule

La suite (u _n) converge uniformément sur un intervalle contenant [-5/2, 5/2]. La limite est illustrée en rouge.

Pour comprendre le mécanisme de la preuve, illustrons le sur un cas particulier d'équation différentielle définissant la courbe logistique, avec la condition de Cauchy C :

On définit une suite de fonctions polynomiales (u_n) par récurrence :

Sur l'intervalle [-5/2, 5/2], la suite (u_n) converge uniformément. Sa limite est un point fixe de la fonction φ qui à une fonction continue f de [-5/2, 5/2] dans R associe la fonction φ_f :

En réitérant la même méthode, on finit par obtenir une solution maximale.

En dérivant l'égalité φ_u = u, on vérifie que u est bien une solution de l'équation différentielle étudiée et par construction u(0) = 1/2. Cette démarche est celle de la démonstration de Lindelöf. Il constate que si l'intervalle est bien choisi, la fonction φ vérifie la condition de Lipschitz avec un coefficient strictement plus petit que 1, elle est donc contractante, ce qui permet de faire usage du théorème du point fixe. Comme une application contractante n'admet qu'un unique point fixe, l'unicité d'une solution locale est démontrée.

Cette méthode permet de trouver localement une solution. En revanche, pour la valeur 3, la suite (u_n) diverge. Cependant rien n'empêche de répéter la même démarche avec les deux conditions de Cauchy (5/2, u(5/2)) et (-5/2, u(-5/2)), il devient ainsi possible de prolonger la solution. Quitte à réitérer la démarche une infinité de fois, on finit par obtenir une solution maximale.

L'intérêt de la démarche est surtout théorique. Dans le cas particulier de l'exemple, il est aisé d'intégrer directement l'équation différentielle^{[Note 11]}. Dans le cas général, il existe des méthodes plus rapides pour obtenir une approximation de la solution, comme celle d'Euler décrite dans la partie histoire ou encore celle de Runge-Kutta. En revanche, il est possible de démontrer dans le cadre général du théorème de l'article qu'une fonction construite de la même manière que φ est contractante, ce qui montre l'existence et l'unicité d'un point fixe, solution de l'équation différentielle. Cette démarche, caractéristique de l'analyse fonctionnelle, permet de démontrer un résultat plus fort que celui qu'avait démontré Cauchy.

Solution locale d'une équation différentielle autonome

Au lieu d'attaquer directement le cas général, il est plus simple de considérer uniquement une équation différentielle autonome sans paramètre^[36]. Les formulations plus générales du théorème se déduisent de ce cas particulier. Dans ce paragraphe, la fonction f ne dépend pas de la variable t, autrement dit, l'équation (1) s'écrit : x'(t) = f(x(t)) et Ω désigne maintenant un ouvert de E. Si s(t) est une solution, on remarque que l'application qui à t associe s(t + t₀) est aussi une solution, si t₀ est un réel quelconque. Pour cette raison on peut sans perte de généralité supposer que t₀ = 0, ce qui revient à choisir la condition de Cauchy C : x(0) = x₀.

L'objectif de ce paragraphe est de montrer que l'équation (1) admet localement une unique solution satisfaisant la condition de Cauchy C. On suppose que f est localement lipschitzienne . Comme Ω est un ouvert, il existe un réel strictement positif a tel que la boule, noté B, fermée de centre x₀ et de rayon a soit inclus dans Ω et telle que la restriction à cette boule de la fonction f soit k-lipschitzienne avec k strictement supérieur à 0^{[Note 12]}. Soit m un majorant strictement positif de la norme de f sur B, qui existe car f est k-lipschitzienne sur B. Soit enfin b un réel positif, strictement plus petit que a/m et que 1/k. Ce réel b permet de définir un espace de fonctions sur lequel on construit une application Φ satisfaisant au théorème du point fixe.

Soit F_x0 l'ensemble des fonctions de [-b, b] à valeurs dans B, m-lipschitziennes et dont l'image de 0 soit égale à x₀.

• Lemme 1 : Munis de la norme de la convergence uniforme, F_x0 est un espace complet.

Il devient maintenant possible de définir de manière générale la fonction Φ. C'est une fonction définie sur F_x0, qui à la fonction u associe la fonction Φ_u définie par :

Deux lemmes sont nécessaires pour pouvoir appliquer le théorème du point fixe :

• Lemme 2 : La fonction Φ est à valeurs dans F_x0.

Une application est dite contractante lorsqu'elle est α-lipschitzienne avec α strictement plus petit que 1.

• Lemme 3 : La fonction Φ est contractante.

Les hypothèses du théorème du point fixe sont réunies, on en déduit que Φ admet un unique point fixe s dans F_x0. En remarquant que la fonction qui à τ associe f(s(τ)) est continue on en déduit que s est une application continument dérivable et de dérivée égale à f(s(τ)). En dérivant l'égalité définissant Φ_s, on en déduit l'existence et l'unicité d'une fonction de F_x0 qui vérifie :

Ce qui se résume en un premier théorème :

• Théorème : Il existe une unique fonction définie sur ]-b, b[ solution de l'équation (1) et vérifiant la condition de Cauchy C.^{[Note 13]}

Si f est de classe C^p, alors la dérivée de s est la composée de deux applications dérivables et elle est dérivable. De proche en proche, on déduit que la dérivée de s est dérivable p fois car composée de deux applications dérivables p fois. Ceci montre que s est de classe C^p.

Une méthode pratique pour trouver le point fixe est de construire une suite (u_n) qui vérifie la relation de récurrence : u_n+1 = Φ_un, la suite converge nécessairement vers le point fixe. Cette technique est celle utilisée dans le préambule.

Démonstrations des lemmes

• Munis de la norme de la convergence uniforme, F_x0 est un espace complet :

Pour montrer ce lemme, il suffit de montrer qu'une suite de Cauchy (u_n) de F_x0 converge vers un élément de F_x0. L'espace des fonctions continues définie sur [-b, b] et à valeurs B est complet car B l'est. La suite (u_n) admet donc une limite u à valeurs dans B. Comme l'image par u de 0 est égal à x₀, car la suite (u_n(0)) est constante, il suffit de montrer que cette limite est m-Lipschitzienne. Le fait que la suite (u_n) converge uniformément vers u montre que si ε est un réel strictement positif :

Le fait que toutes les fonctions de F_x0 soient m-lipschitziennes, montre que :

On en déduit, si n est un entier plus grand que N :

La dernière majoration est vraie pour tout ε strictement positif, ce qui montre que la fonction u est bien m-lipschitzienne.

• La fonction Φ est à valeurs dans F_x0 :

Soit u une fonction de F_x0, Φ_u est une fonction à valeurs dans E dont l'image de 0 est égale à x₀. Il suffit de montrer qu'elle prend ses valeurs dans B et qu'elle est m-lipschitzienne. Montrons dans un premier temps qu'elle est m-lipschitzienne. Soient t₁ et t₂ deux éléments de [-b, b], on a :

La dernière majoration montre que Φ_u est m-lipschitzienne, il reste à montrer qu'elle est à valeurs dans B. Soit t un élément de [-b, b], il faut montrer que Φ_u(t) est à une distance inférieure ou égale à a de x₀ :

Cette dernière majoration montre que Φ_u est à valeurs dans B et termine la démonstration du lemme.

• La fonction Φ est contractante :

Soit u et v deux fonctions de F_x0, déterminons la distance entre leurs deux images par Φ. Soit t un élément de [-b, b] :

Par définition de b, le réel bk est strictement plus petit que 1, ce qui montre le caractère contractant de Φ.

 

Solution maximale d'une équation différentielle autonome

À l'exception de l'unicité de la solution locale, le paragraphe précédent résume le résultat démontré à l'époque de Cauchy^{[Note 14]}. Il n'offre aucune information sur l'existence ou l'unicité d'une solution globale vérifiant la condition de Cauchy C. Ces résultats, plus tardifs, sont presque une conséquence directe du paragraphe précédent. On peut les résumer de la manière suivante^[37], si f est autonome et que t₀ = 0 :

• Théorème : Il existe une unique solution de l'équation (1), vérifiant la condition C et maximale. Tout autre solution, définie sur un intervalle J, est confondue avec la restriction de la solution maximale sur J et J est inclus dans l'intervalle de définition de la solution maximale.

• Proposition : L'intervalle de définition d'une solution maximale est ouvert.

Équation différentielle non autonome

À l'aide d'un habile jeu d'écriture^[38], il est possible de généraliser le cas particulier précédent aux équations dépendantes du temps. On considère maintenant l'équation (1) du théorème, associée à la condition de Cauchy C. Soit g, la fonction de Ω dans l'espace de Banach RxE, définie par :

Si y₀ désigne le point de Ω égal à (t₀, x₀), on considère l'équation différentielle et la condition de Cauchy suivante :

La fonction g est localement lipschitzienne si f l'est. En effet, si y est un élément de Ω, il existe un voisinage V de y et le réel k strictement positif associée à f (qui est localement lipschitzienne par rapport à la deuxième variable) est tel que, si les coordonnées d'un point y₁ (resp. y₂) de V, sont notées ((t₁, x₂) (resp. (t₂, x₂)), on a :

L'énoncé du théorème de l'article ne se déduit pas immédiatement de ce calcul. Le théorème général ne suppose pas que f est localement lipschitzienne, mais uniquement que f continue et localement lipschitzien par rapport à la deuxième variable^[39]. En fait, pour se rendre compte que ces hypothèses suffisent, il suffit de remarquer que le caractère lipschitzien n'intervient qu'à deux endroits, dans la démonstration.

Dans un premier temps, il apparaît nécessaire que l'image par g de la boule B soit majorée. Remarquons tout d'abord, avec les notations des paragraphes précédents, que la fonction de [-b, b] dans Ω, qui à t associe ||f(t, x₀)|| est continue définie sur un compact et à valeurs dans R⁺, elle est donc majorée. Soit m₁ un tel majorant. Montrons maintenant que g est borné sur B. Soit y égal à (t,x) un point de B :

On dispose donc d'un majorant de la norme de g(y) indépendant de y si y est un élément de B.

Le deuxième endroit de la démonstration où le caractère lipschitzien apparait est celui qui prouve que la fonction φ (maintenant définie à l'aide de la fonction g) est bien contractante. Cette fois ci, F_x0 est l'ensemble des fonctions u₁(t) de [-b + t₀, b + t₀] dans B, qui à t associe (t, u(t)) où u(t) est une fonction m-lipschitzienne, à valeurs dans E et qui vaut x₀ en t₀. Les mêmes calculs montrent que F_x0 est stable par φ et que φ est bien contractant. Pour montrer que φ est contractant, on considère encore deux fonctions u₁ et v₁ de F_x0 :

Annexes

Voir aussi

• Théorème de Cauchy-Peano-Arzelà
• Critère de Nagumo

Bibliographie

• J. M. Arnaudiès, Équations différentielles de fonctions de variable réelle ou complexe, Ellipse, 2000 (ISBN 9782729800451)
  Ce livre présente une première approche du théorème. Il correspond à un contenu général sur les équations différentielles, commun à tous les cours de licences sur cette question.

• Marcel Berger et Bernard Gostiaux, Géométrie différentielle : variétés, courbes et surfaces [détail des éditions] 
  Ce livre présente une approche un peu plus complète. Elle se limite au cas où E est un espace vectoriel de dimension finie, mais va plus loin que la présentation générale car traite aussi de l'équation sous forme de flot et montre la continuité du flot. Cette référence a guidé la construction de la partie démonstrations de l'article.

• Jean-Pierre Demailly, Analyse numérique et équations différentielles [détail des éditions]

• S. Lang, Analyse Réelle, InterEditions, Paris, 1977 (ISBN 2729600595)
  Ce livre est plus complet puisque le cas général des espaces de Banach est traité, ainsi que le caractère C^p du flot.

• P. Malliavin, Géométrie différentielle intrinsèque, Hermann, 1972 (ISBN 978-2705656966)
  Cette référence est encore plus complète, mais plus ardue que la précédente. On y trouve les démonstrations associées au cas où le champ de vecteurs est infiniment différentiable.

• (en) S. Lang, Analysis II, Addison-Wesley Chap, 1969
  Cette référence est relativement complète, et d'orientation moins géométrique que la précédente.

• D. Leborgne, Calcul différentiel et géométrie, Puf, 1982 (ISBN 2130374956)
  Ce livre suppose déjà connu le théorème dans le cas des espaces de Banach ; il le généralise aux variétés différentielles.

• Lev Pontriaguine, Équations différentielles ordinaires, Moscou, Éditions Mir, 1969; (un des meilleurs livres, en français, sur le sujet avec un exposé très clair sur l'application de Poincaré utilisée dans la théorie du chaos).

Liens externes

Histoire

• A. L. Cauchy, Leçons de calcul différentiel et intégral, 26^e leçon, pp 385-396

Mathématiques

• F. Paulin, Théorie de Cauchy-Lipschitz, École Normale Supérieure, p. 228-244
  Ce site propose une vision complète de la théorie. Elle est plus générale que l'article car elle traite aussi de l'équation différentielle linéaire et du flot.

• A. Popier, O. Wintenberger, Équations différentielle, École Polytechnique
  Ce site propose une vision plus partielle de la théorie que le site précédent. Seule la régularité de la courbe intégrale est étudiée, celle du flot n'est pas abordée. En revanche, l'hypothèse de la seule continuité de f est étudié, la version de Peano-Arzelà est démontrée.

• N. Petit, P. Rouchon, Théorème de Cauchy, École des Mines de Paris, p. 203
  Ce site présente une vision plus simple. La méthode de l'approximation d'Euler est utilisée au détriment de celle du point fixe. Seuls les théorèmes d'existence de solutions intégrales sont traités.

Notes

Références

Cet article est reconnu comme « bon article » depuis sa version du 20 avril 2009 (comparer avec la version actuelle). Pour toute information complémentaire, consulter sa page de discussion et le vote l’ayant promu. La version du 20 avril 2009 de cet article a été reconnue comme « bon article », c'est-à-dire qu'elle répond à des critères de qualité concernant le style, la clarté, la pertinence, la citation des sources et l'illustration.

• Portail de l'analyse