Théorème de Cauchy-Kovalevskaïa

Théorème de Cauchy-Kovalevskaïa

Théorème de Cauchy-Kowalevski

Page d'aide sur l'homonymie Pour les articles homonymes, voir Cauchy.

Le théorème de Cauchy-Kowalevski est un théorème d'analyse à plusieurs variables stipulant qu'une équation aux dérivées partielles du type équation de Klein-Gordon est bien posée, c'est-à-dire que cette équation admet une solution unique si les conditions initiales sur les fonctions concernées sont bien posées. Il est l'œuvre du mathématicien français Augustin Cauchy pour un cas particulier, et de Sofia Kovalevskaïa pour le cas général.

Plus précisément, ce théorème peut s'énoncer ainsi :

Théorème — Soient t, x1, x2,... xn − 1 des coordonnées de Rn. Si l'on considère un système de m équations aux dérivées partielles portant sur des fonctions φi, de la forme

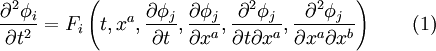\frac{\partial^2 \phi_i}{\partial t^2} = F_i\left(t, x^a, \frac{\partial\phi_j}{\partial t}, \frac{\partial\phi_j}{\partial x^a}, \frac{\partial^2\phi_j}{\partial t \partial x^a}, \frac{\partial^2\phi_j }{\partial x^a\partial x^b}\right)\qquad(1),

où les fonctions Fi sont des fonctions analytiques de leurs variables, alors, si l'on se donne des fonctions analytiques fi(xa) et gi(xa), il existe un voisinage ouvert O de l'hypersurface t = t0 dans lequel il existe une solution analytique unique de (1) telle que

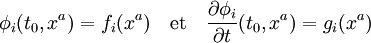\phi_i(t_0, x^a) = f_i(x^a) \quad{\text{et}}\quad \frac{\partial \phi_i}{\partial t}(t_0, x^a) = g_i (x^a).

Le théorème de Cauchy-Kowalevski assure qu'une équation de type Klein-Gordon peut être bien posée au sens mathématique du terme (c'est-à-dire qu'il en existe une solution unique une fois les conditions initiales connues), du moins quand les conditions initiales (sur φ et sa dérivée temporelle à l'instant initial) sont analytiques. Le théorème reste cependant relativement faible. En particulier, il ne précise pas si la solution de l'équation est analytique, ou même simplement continue vis-à-vis des conditions initiales. Plus important, il ne précise pas non plus si une équation du type Klein-Gordon se comporte de façon causale. Par exemple, si le champ est nul sur un intervalle [ − x,x] à l'instant t0, l'on s'attend à ce que le champ reste nul en 0 jusqu'au temps t0 + x / c, ce que le théorème de Cauchy-Kowalevski ne précise pas (ne serait-ce que parce qu'une telle condition initiale serait non analytique et ne saurait être traitée par ce théorème).

Référence

Lien externe

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de Cauchy-Kowalevski ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Cauchy-Kovalevskaïa de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Théorème de Cauchy-Kowalevski — Pour les articles homonymes, voir Cauchy. Le théorème de Cauchy Kowalevski est un théorème d analyse à plusieurs variables stipulant qu une équation aux dérivées partielles du type équation de Klein Gordon est bien posée, c est à dire que cette… …   Wikipédia en Français

  • Théorème de Cauchy-Lipschitz — Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. En mathématiques, et plus précisément en a …   Wikipédia en Français

  • Théorème de Cauchy (groupes) — Pour les articles homonymes, voir Cauchy. En mathématiques, le théorème de Cauchy fournit l existence d éléments d ordre diviseur premier du cardinal d un groupe fini. Il est nommé ainsi en l honneur du mathématicien Augustin Louis Cauchy.… …   Wikipédia en Français

  • Theoreme de Cauchy-Kowalevski — Théorème de Cauchy Kowalevski Pour les articles homonymes, voir Cauchy. Le théorème de Cauchy Kowalevski est un théorème d analyse à plusieurs variables stipulant qu une équation aux dérivées partielles du type équation de Klein Gordon est bien… …   Wikipédia en Français

  • Théorème de Cauchy-Kovalevskaya — Théorème de Cauchy Kowalevski Pour les articles homonymes, voir Cauchy. Le théorème de Cauchy Kowalevski est un théorème d analyse à plusieurs variables stipulant qu une équation aux dérivées partielles du type équation de Klein Gordon est bien… …   Wikipédia en Français

  • Théorème de cauchy-kowalevski — Pour les articles homonymes, voir Cauchy. Le théorème de Cauchy Kowalevski est un théorème d analyse à plusieurs variables stipulant qu une équation aux dérivées partielles du type équation de Klein Gordon est bien posée, c est à dire que cette… …   Wikipédia en Français

  • Kovalevskaïa — Sofia Kovalevskaïa Sofia Kovalevskaïa Sofia Vassilievna Kovalevskaïa (également Sonia, Sofa ; en russe : Софья Васильевна Ковалевская ; en français et en allemand elle signe Sophie Kowalevski) est une mathématicienne russe née à… …   Wikipédia en Français

  • Théorème intégral de Cauchy — Pour les articles homonymes, voir Cauchy. En analyse complexe, le théorème intégral de Cauchy est un important résultat concernant les intégrales curvilignes de fonctions holomorphes dans le plan complexe. D après ce théorème, si deux chemins… …   Wikipédia en Français

  • Sofia Kovalevskaïa — Naissance 15 janvier 1850 Moscou (Russie) Décès 10 février 1891 …   Wikipédia en Français

  • Sofia Kovalevskaia — Sofia Kovalevskaïa Sofia Kovalevskaïa Sofia Vassilievna Kovalevskaïa (également Sonia, Sofa ; en russe : Софья Васильевна Ковалевская ; en français et en allemand elle signe Sophie Kowalevski) est une mathématicienne russe née à… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”