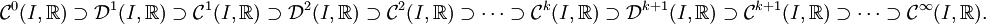Classe De Régularité
- Classe De Régularité
-
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Classe De Régularité de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Classe de regularite — Classe de régularité En mathématiques, les différentes classes de régularité sont définies à partir des dérivées itérées des fonctions, et de la continuité éventuelle de ces dérivées. Si I est un intervalle de , et un entier on note l ensemble… … Wikipédia en Français
Classe de régularité — En mathématiques et en analyse, les classes de régularité des fonctions numériques constituent un catalogue fragmentaire basé sur l’existence et la continuité des dérivées itérées, sans se préoccuper de la forme ou de l’allure de la fonction… … Wikipédia en Français
Régularité par morceaux — En mathématiques, les énoncés de certaines propriétés d analyse et résultats de convergence se réfèrent à des fonctions vérifiant des hypothèses telles que continues par morceaux, dérivables par morceaux, etc. Ces fonctions sont regroupées par… … Wikipédia en Français
Regularite par morceaux — Régularité par morceaux Certaines propriétés d analyse sont énoncées avec des fonctions vérifiant des hypothèses telles que continu par morceaux, de classe par morceaux, etc. Régularité par morceaux sur un segment Une fonction f est continue par… … Wikipédia en Français
Classes de régularité — Classe de régularité En mathématiques, les différentes classes de régularité sont définies à partir des dérivées itérées des fonctions, et de la continuité éventuelle de ces dérivées. Si I est un intervalle de , et un entier on note l ensemble… … Wikipédia en Français
Fonction de classe C-infini — Dérivation itérée En mathématiques, le concept de dérivation itérée étend le concept de dérivée en le répétant plusieurs fois. Sommaire 1 Définition 1.1 Dérivée première sur un intervalle 1.2 Dérivée seconde sur un intervalle … Wikipédia en Français
Fonction de classe C1 — Dérivation itérée En mathématiques, le concept de dérivation itérée étend le concept de dérivée en le répétant plusieurs fois. Sommaire 1 Définition 1.1 Dérivée première sur un intervalle 1.2 Dérivée seconde sur un intervalle … Wikipédia en Français
Fonction de classe C2 — Dérivation itérée En mathématiques, le concept de dérivation itérée étend le concept de dérivée en le répétant plusieurs fois. Sommaire 1 Définition 1.1 Dérivée première sur un intervalle 1.2 Dérivée seconde sur un intervalle … Wikipédia en Français
Fonction de classe Cn — Dérivation itérée En mathématiques, le concept de dérivation itérée étend le concept de dérivée en le répétant plusieurs fois. Sommaire 1 Définition 1.1 Dérivée première sur un intervalle 1.2 Dérivée seconde sur un intervalle … Wikipédia en Français
Rallye De Régularité — BMW 2002 tii … Wikipédia en Français
 , et
, et 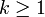 un entier on note
un entier on note 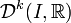 l'ensemble des fonctions de I vers
l'ensemble des fonctions de I vers  qui sont k fois dérivables. On note
qui sont k fois dérivables. On note 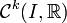 le sous-ensemble de
le sous-ensemble de 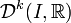 formé par les fonctions dont la k-ième dérivée est continue, et on note
formé par les fonctions dont la k-ième dérivée est continue, et on note 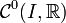 l'ensemble des fonctions continues de I vers
l'ensemble des fonctions continues de I vers  . Enfin on note
. Enfin on note 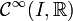 l'ensemble des fonctions indéfiniment dérivables de I vers
l'ensemble des fonctions indéfiniment dérivables de I vers  .
. et on a la suite d'inclusions :
et on a la suite d'inclusions :