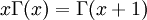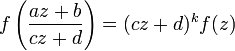Equation fonctionnelle
- Equation fonctionnelle
-
Équation fonctionnelle
En mathématiques, une équation fonctionnelle est une équation dont les inconnues sont des fonctions. De nombreuses propriétés de fonctions peuvent être déterminées en étudiant quelles équations elles satisfont. D'habitude, le terme « équation fonctionnelle » est réservé aux équations qu'on ne peut pas ramener à une équation algébrique, le plus souvent parce que la fonction cherchée a pour arguments dans l'équation, non pas directement la variable, mais des fonctions (déterminées) de la variable elle-même.
Exemples
-

- est satisfaite par la fonction Zeta de Riemann. La lettre Γ désigne la fonction Gamma d'Euler.
-
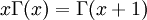
- est satisfaite par la fonction Gamma d'Euler.
-
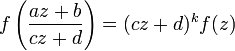
- où a, b, c et d sont des entiers naturels vérifiant ad − bc = 1, se retrouve dans la définition du concept de forme modulaire.
- D'autres exemples d'équations fonctionnelles :
-
- f(x + y) = f(x)f(y), satisfaite par les fonctions exponentielles
-
- f(xy) = f(x) + f(y), satisfaite par les fonctions logarithmes
-
- f(x + y) = f(x) + f(y) (équation de Cauchy)
-
- F(az) = aF(z)(1 − F(z)) (équation de Poincaré)
-
- G(x) = λ−1 G(G(λz)) (théorie du chaos)
-
- f((x + y)/2) = (f(x) + f(y))/2 (Jensen)
-
- g(x + y) + g(x − y) = 2g(x)g(y) (d'Alembert)
-
- f(h(x)) = f(x) + 1 (Abel)
-
- f(h(x)) = cf(x) (Schröder).
- L'équation de Schröder est satisfaite par la fonction de Koenigs.
- Une forme simple d'équation fonctionnelle est la relation de récurrence, qui comprend une fonction inconnue définie sur l'ensemble des entiers et l'opérateur de translation.
- Un exemple de relation de récurrence :
-
- a(n) = 3a(n − 1) + 4a(n − 2)
- Les lois commutatives et associatives sont des équations fonctionnelles. Quand la loi associative est exprimée sous sa forme habituelle, on représente une opération binaire par un symbole entre les deux variables, comme suit:
-
- (a * b) * c = a * (b * c),
- Mais si l'on écrit f(a, b) au lieu de a * b, alors la loi associative ressemble plus à ce que l'on entend conventionnellement par "équation fonctionnelle":
-
- f(f(a, b), c) = f(a, f(b, c)).
Un point commun à tous ces exemples est que dans chacun des cas, deux ou plusieurs fonctions (tantôt la multiplication par une constante, tantôt l'addition de deux variables, tantôt la fonction identité) sont substituées à l'inconnue.
Quand il est question de trouver toutes les solutions, il arrive que certaines conditions analytiques soient exigées ; par exemple, dans le cas de l'équation de Cauchy, les solutions continues sont les solutions raisonnables alors que les autres solutions sont plus difficilement accessibles. Le théorème de Bohr-Mollerup est un autre exemple connu.
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Equation fonctionnelle de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Équation fonctionnelle — En mathématiques, une équation fonctionnelle est une équation dont les inconnues sont des fonctions. De nombreuses propriétés de fonctions peuvent être déterminées en étudiant quelles équations elles satisfont. D habitude, le terme… … Wikipédia en Français
équation fonctionnelle — funkcionalinė lygtis statusas T sritis fizika atitikmenys: angl. functional equation vok. Funktionalgleichung, f rus. функциональное уравнение, n pranc. équation fonctionnelle, f … Fizikos terminų žodynas
équation fonctionnelle — operatorinė lygtis statusas T sritis fizika atitikmenys: angl. operator equation vok. Operatorengleichung, f rus. операторное уравнение, n pranc. équation fonctionnelle, f … Fizikos terminų žodynas
Equation fonctionnelle (fonction L) — Équation fonctionnelle (fonction L) En mathématiques, les fonctions L de la théorie des nombres ont certaines équations fonctionnelles, comme une de leur propriétés caractéristiques. Il existe une théorie élaborée de ce qu elles devraient être;… … Wikipédia en Français
Équation fonctionnelle (fonction l) — En mathématiques, les fonctions L de la théorie des nombres ont certaines équations fonctionnelles, comme une de leur propriétés caractéristiques. Il existe une théorie élaborée de ce qu elles devraient être; beaucoup d entre elles sont encore… … Wikipédia en Français
Équation fonctionnelle (fonction L) — En mathématiques, l une des propriétés caractéristiques des fonctions L de la théorie des nombres est la forme de leur équation fonctionnelle. Il existe une théorie élaborée de ce que devraient être ces propriétés ; beaucoup d entre elles… … Wikipédia en Français
Équation fonctionnelle de Cauchy — L’équation fonctionnelle de Cauchy est l une des équations fonctionnelles les plus simples, elle s écrit : d inconnue En d autres termes, les solutions de cette équation sont exactement les endormorphismes de . On montre aisément que f est… … Wikipédia en Français
Equation differentielle — Équation différentielle En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de différenciation auquel une… … Wikipédia en Français
Equation différentielle — Équation différentielle En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de différenciation auquel une… … Wikipédia en Français
Équation différentielle du premier ordre — Équation différentielle En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de différenciation auquel une… … Wikipédia en Français