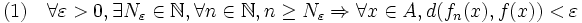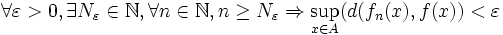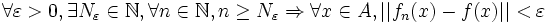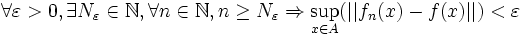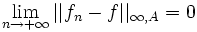- Convergence Uniforme
-
Convergence uniforme
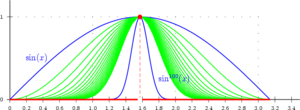
 Suite de fonctions convergeant uniformément vers la fonction valeur absolue.
Suite de fonctions convergeant uniformément vers la fonction valeur absolue.
La convergence uniforme d'une suite de fonctions
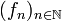 est une forme de convergence plus exigeante que la convergence simple. Cette dernière demande en effet seulement que, pour chaque point x, la suite
est une forme de convergence plus exigeante que la convergence simple. Cette dernière demande en effet seulement que, pour chaque point x, la suite 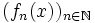 ait une limite. La convergence devient uniforme quand toutes les suites
ait une limite. La convergence devient uniforme quand toutes les suites 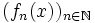 avancent vers leur limite respective avec une sorte de « mouvement d'ensemble ».
avancent vers leur limite respective avec une sorte de « mouvement d'ensemble ».Dans le cas de fonctions numériques d'une variable, la notion prend une forme d'évidence géométrique : le graphe de la fonction fn se « rapproche » de celui de la limite.
Sommaire
Définition
Convergence uniforme
- Soient
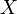 un espace topologique,
un espace topologique, 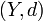 un espace métrique et
un espace métrique et 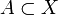 un sous-ensemble de
un sous-ensemble de 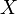 .
.
Soit
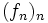 une suite de fonctions définies sur
une suite de fonctions définies sur 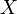 et à valeurs dans
et à valeurs dans  et
et 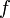 une fonction définie sur
une fonction définie sur 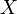 à valeurs dans
à valeurs dans  . On dit que la suite
. On dit que la suite 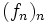 converge uniformément vers
converge uniformément vers  sur
sur 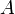 si :
si :Remarque : la proposition
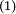 est équivalente à :
est équivalente à :Quelques explications
On peut se demander a posteriori quelle est la différence entre la convergence simple d'une suite de fonctions et la convergence uniforme. En effet, la suite de fonctions
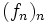 converge simplement vers
converge simplement vers  sur
sur 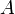 si :
si :Ici, l'indice
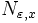 dépend de
dépend de  alors que dans la proposition
alors que dans la proposition 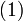 , l'indice
, l'indice 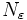 n'en dépend pas. Cette différence peut paraître anodine aux non-initiés, mais elle est pourtant essentielle:
n'en dépend pas. Cette différence peut paraître anodine aux non-initiés, mais elle est pourtant essentielle:- Dans le cas de la convergence simple, pour tout élément
 , on peut trouver un rang à partir duquel la distance
, on peut trouver un rang à partir duquel la distance 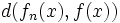 devient très petite. A priori, si on choisit un
devient très petite. A priori, si on choisit un  autre que x alors le rang à partir duquel la distance
autre que x alors le rang à partir duquel la distance 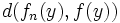 devient très petite va être différent.
devient très petite va être différent. - Dans le cas de la convergence uniforme, on peut trouver un rang à partir duquel la distance
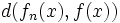 devient très petite pour n'importe quel
devient très petite pour n'importe quel  à la fois. Cette condition est donc beaucoup plus forte. En particulier, une suite de fonctions qui converge uniformément sur un ensemble converge simplement sur celui-ci. La réciproque est en général fausse sauf dans des cas très particuliers (voir Théorèmes de Dini).
à la fois. Cette condition est donc beaucoup plus forte. En particulier, une suite de fonctions qui converge uniformément sur un ensemble converge simplement sur celui-ci. La réciproque est en général fausse sauf dans des cas très particuliers (voir Théorèmes de Dini).
Critère de Cauchy uniforme
Maintenant, on suppose en plus que l'espace métrique
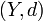 est un espace complet. C'est le cas de bon nombre d'espaces métriques, comme par exemple de
est un espace complet. C'est le cas de bon nombre d'espaces métriques, comme par exemple de 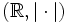 la droite réelle munie de sa valeur absolue ou encore plus généralement de tout espace de Banach.
la droite réelle munie de sa valeur absolue ou encore plus généralement de tout espace de Banach.Sous ces conditions, une suite de fonctions
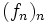 converge uniformément sur
converge uniformément sur 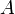 si et seulement si elle vérifie le critère de Cauchy uniforme, à savoir :
si et seulement si elle vérifie le critère de Cauchy uniforme, à savoir :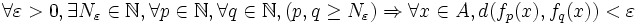
Comme dans le cas des suites de Cauchy, il n'est pas nécessaire d'exhiber la fonction vers laquelle tend une suite de fonctions pour montrer que la convergence est uniforme.
Pour s'en rendre compte, il suffit de remarquer que pour tout x, la suite
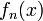 converge car elle est de Cauchy dans un espace complet. Notons
converge car elle est de Cauchy dans un espace complet. Notons  sa limite. On choisit une valeur
sa limite. On choisit une valeur  strictement supérieure à 0, Il existe un entier N tel que :
strictement supérieure à 0, Il existe un entier N tel que :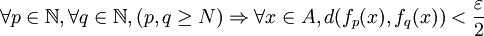
Pour chaque x, il existe un entier
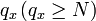 telle que :
telle que : 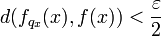
Autrement dit :
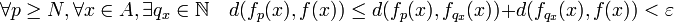
La dernière majoration montre la convergence uniforme. Ainsi si une suite vérifie le critère de Cauchy uniforme elle est uniformément convergente. Réciproquement, toute suite convergente vérifie nécessairement le critère de Cauchy, ce qui termine la démonstration.
Convergence uniforme de fonctions à valeurs dans un espace vectoriel normé
On suppose maintenant que
 est un espace métrique et que
est un espace métrique et que  est un espace vectoriel normé : c'est un espace métrique dont la topologie est issue de la distance
est un espace vectoriel normé : c'est un espace métrique dont la topologie est issue de la distance 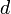 telle que :
telle que :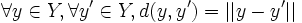 .
.
La convergence uniforme d'une suite de fonctions
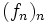 sur une partie
sur une partie 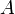 inclus dans
inclus dans 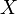 s'écrit donc :
s'écrit donc :Ce qui est encore équivalent à :
Théorèmes
On a le résultat fondamental suivant:
Si
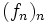 est une suite de fonctions continues convergeant uniformément sur
est une suite de fonctions continues convergeant uniformément sur 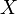 vers une fonction
vers une fonction  alors
alors  est continue sur
est continue sur 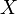 .
.Preuve. Soit
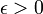 donné. Il existe un entier
donné. Il existe un entier 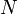 tel que, pour tout
tel que, pour tout 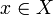 ,
, 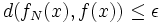 . La fonction
. La fonction  est continue en tout point
est continue en tout point 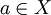 . Il existe ainsi un ouvert
. Il existe ainsi un ouvert 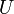 contenant
contenant  tel que
tel que  pour tout
pour tout  . Alors, si
. Alors, si  ,
,
Quand
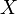 n'est pas compact, la convergence uniforme est un phénomène rare. Par exemple,
n'est pas compact, la convergence uniforme est un phénomène rare. Par exemple, 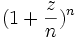 converge uniformément vers
converge uniformément vers 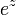 sur tout compact de
sur tout compact de  quand l'entier
quand l'entier 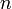 tend vers l'infini, mais pas sur
tend vers l'infini, mais pas sur  ; une série entière de rayon de convergence
; une série entière de rayon de convergence 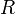 converge uniformément sur tout compact du disque ouvert de centre 0 et de rayon
converge uniformément sur tout compact du disque ouvert de centre 0 et de rayon 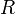 , mais on ne peut pas dire mieux en général.
, mais on ne peut pas dire mieux en général.En fait, la continuité étant une propriété locale, la convergence uniforme sur "suffisamment" de parties de
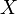 suffit à assurer la continuité de la fonction limite.
suffit à assurer la continuité de la fonction limite.Exemples
- Lorsque
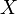 est localement compact, ou lorsque sa topologie est définie par une métrique.
est localement compact, ou lorsque sa topologie est définie par une métrique.
Dans ces conditions, si une suite
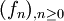 de fonctions continues converge uniformément sur tout compact vers une fonction
de fonctions continues converge uniformément sur tout compact vers une fonction  , alors
, alors  est continue.
est continue.- On a la même conclusion lorsque
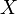 est un espace de Banach, si la convergence uniforme a lieu
est un espace de Banach, si la convergence uniforme a lieu
sur toute boule fermée de centre
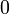 . C'est ainsi que l'on démontre par exemple la continuité de la fonction exponentielle dans une algèbre de Banach.
. C'est ainsi que l'on démontre par exemple la continuité de la fonction exponentielle dans une algèbre de Banach.Le résultat suivant, moins fort que le théorème de convergence dominée, est aussi beaucoup moins difficile à montrer.
Si
![X=[a,b]\,](/pictures/frwiki/98/b7e937072657d67b041d537e9ac3c695.png) est un intervalle de
est un intervalle de  , si
, si 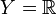 ou
ou  , alors si une suite de fonctions
, alors si une suite de fonctions 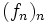 intégrables converge uniformément vers une fonction
intégrables converge uniformément vers une fonction  intégrable alors :
intégrable alors : 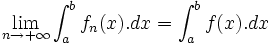 .
.Son utilisation est à la base du résultat suivant d'analyse complexe.
Soit
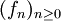 une suite de fonctions holomorphes sur un ouvert de
une suite de fonctions holomorphes sur un ouvert de 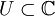 , convergeant uniformément sur tout compact de
, convergeant uniformément sur tout compact de 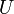 vers une fonction
vers une fonction  . Alors
. Alors  est holomorphe.
est holomorphe.Notation
On introduit la notation suivante :
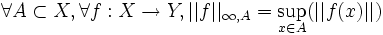
Il s'ensuit directement qu'une suite de fonctions
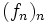 converge uniformément vers une fonction
converge uniformément vers une fonction  si et seulement si :
si et seulement si :
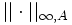 n'est en général pas une norme sur l'espace vectoriel des fonctions de
n'est en général pas une norme sur l'espace vectoriel des fonctions de  à valeurs dans
à valeurs dans  .
.Cas où X est compact
On suppose désormais que X est un espace métrique compact,
 étant toujours un espace vectoriel normé. On note
étant toujours un espace vectoriel normé. On note  l'ensemble des fonctions continues définies sur
l'ensemble des fonctions continues définies sur 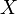 et à valeurs dans
et à valeurs dans 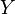 .
.Alors :
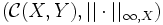 est un espace vectoriel normé. Si de plus,
est un espace vectoriel normé. Si de plus, 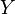 est complet alors
est complet alors  est lui aussi complet.
est lui aussi complet.Critères de convergence uniforme pour les séries
Dans cette section, il n'est envisagé que le cas des fonctions réelles d'une variable réelle.
On trouve dans la littérature[1] la mention de nombreux tests de convergence uniforme portant les noms d'Abel, de Dedekind, de du Bois-Reymond, de Dirichlet, de Weierstrass... Ces critères sont des critères pratiques, cas particuliers de la formule de sommation partielle d'une série, plus faciles à appliquer.
Critère de Weierstrass
« La série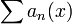 converge uniformément dans l'intervalle I si les fonctions an(x) sont chacune majorées en valeur absolue sur l'intervalle I par un nombre αn et que la série
converge uniformément dans l'intervalle I si les fonctions an(x) sont chacune majorées en valeur absolue sur l'intervalle I par un nombre αn et que la série 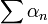 est convergente. »
est convergente. »On dit dans ce cas que l'on a une série normalement convergente.
Critère de convergence uniforme d'Abel
« La série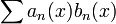 converge uniformément dans l'intervalle I si la série
converge uniformément dans l'intervalle I si la série 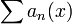 converge uniformément dans I et si de plus, pour toute valeur fixée de x, la suite bn(x) est monotone et enfin s'il existe un nombre K indépendant de x qui majore |b_n(x)| pour tout x de I et tout n. »
converge uniformément dans I et si de plus, pour toute valeur fixée de x, la suite bn(x) est monotone et enfin s'il existe un nombre K indépendant de x qui majore |b_n(x)| pour tout x de I et tout n. »On exprime cette dernière condition en disant que les fonctions bn(x) sont uniformément bornées dans I.
Critère de convergence uniforme de Dirichlet
« La série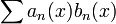 converge uniformément dans l'intervalle I si les sommes partielles de la série
converge uniformément dans l'intervalle I si les sommes partielles de la série 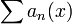 sont uniformément bornées dans I et si les fonctions bn(x) convergent uniformément dans I vers 0, la convergence étant monotone pour tout x fixé. »
sont uniformément bornées dans I et si les fonctions bn(x) convergent uniformément dans I vers 0, la convergence étant monotone pour tout x fixé. »Critère de convergence uniforme de Dedekind
« La série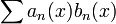 converge uniformément dans l'intervalle I si la série
converge uniformément dans l'intervalle I si la série 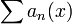 admet des sommes partielles uniformément bornées , les fonctions bn(x) tendent vers 0 uniformément dans I et que la série
admet des sommes partielles uniformément bornées , les fonctions bn(x) tendent vers 0 uniformément dans I et que la série 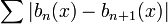 converge uniformément dans I. »
converge uniformément dans I. »Critère de convergence uniforme de Du Bois-Reymond
« La série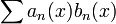 converge uniformément dans l'intervalle I si les séries
converge uniformément dans l'intervalle I si les séries 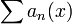 et
et 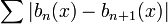 convergent uniformément dans I, les fonctions bn(x) étant de plus uniformément bornées dans I. »
convergent uniformément dans I, les fonctions bn(x) étant de plus uniformément bornées dans I. »Un autre critère
« La série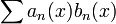 converge uniformément dans l'intervalle I si les séries
converge uniformément dans l'intervalle I si les séries 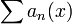 et
et  convergent uniformément dans I, les fonctions bn(x) étant de plus uniformément bornées dans I. »
convergent uniformément dans I, les fonctions bn(x) étant de plus uniformément bornées dans I. »dont un corollaire immédiat est
« La série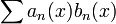 converge uniformément dans l'intervalle I si la série
converge uniformément dans l'intervalle I si la série 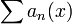 converge uniformément dans I, les fonctions an(x) étant positives et les fonctions bn(x) étant uniformément bornées dans I. »
converge uniformément dans I, les fonctions an(x) étant positives et les fonctions bn(x) étant uniformément bornées dans I. »Espace des fonctions numériques continues sur [a,b]
On choisit dans cette section
![X=[a,b]\,](/pictures/frwiki/98/b7e937072657d67b041d537e9ac3c695.png) un intervalle compact de
un intervalle compact de  et
et 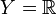 . Puisque
. Puisque  muni de la valeur absolue est complet, il en résulte que l'espace vectoriel normé
muni de la valeur absolue est complet, il en résulte que l'espace vectoriel normé ![\mathcal{C}([a,b],\R)](/pictures/frwiki/55/727479202f7a734eb2d96ce9473d938f.png) muni de la norme
muni de la norme ![||\cdot||_{\infty,[a,b]}](/pictures/frwiki/48/0a8814ac9aa314a8e6b264f1960ddc5d.png) est complet.
est complet.Théorème de Weierstrass
Le théorème de Weierstrass affirme qu'on peut approcher de manière uniforme n'importe quelle fonction numérique continue sur
![[a,b]\,](/pictures/frwiki/55/7f3408c72246eece3d5542fc853ce417.png) par une suite de fonctions très régulières à savoir par des polynômes. Plus précisément, si
par une suite de fonctions très régulières à savoir par des polynômes. Plus précisément, si  est une fonction continue sur
est une fonction continue sur ![[a,b]\,](/pictures/frwiki/55/7f3408c72246eece3d5542fc853ce417.png) alors:
alors:![\forall \varepsilon>0, \exists P_{\varepsilon} \in \R[X], ||f-P_{\varepsilon}||_{\infty,[a,b]}\leq \varepsilon](/pictures/frwiki/97/a3fbe8174f00b7103712e263e77db9b5.png) .
.
où
![\R[X]](/pictures/frwiki/54/60ed190117e7614d227f8d1693161a5b.png) désigne l'ensemble des polynômes à coefficients réels.
désigne l'ensemble des polynômes à coefficients réels.Notes et références
- ↑ Voir par exemple Knopp, theorie und andwendung der unendlichen reihen, 1922, (ou sa traduction, Knopp, Theorie and applications of infinite series, 1954)
Voir aussi
- Portail des mathématiques
Catégories : Analyse fonctionnelle | Espace vectoriel normé - Soient
Wikimedia Foundation. 2010.