- Regle de Cauchy
-
Règle de Cauchy
Pour les articles homonymes, voir Cauchy.La règle de Cauchy, qui doit son nom au mathématicien français Augustin Cauchy, est un critère de convergence pour une série à termes complexes, ou à termes dans un espace de Banach.
On lui donne parfois aussi le nom de « critère de Cauchy » mais il y a risque de confusion avec l'énoncé très utile « toute suite de Cauchy de réels (ou complexes) converge » qui est celui qu'on désigne le plus souvent comme le « critère de Cauchy », et qui peut aussi être écrit pour l'étude des séries.
Énoncé simplifié
Soit
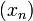une suite à valeurs dans un espace vectoriel normé, par exemple une suite de complexes, et telle que la limite suivante existe :- si p est strictement inférieur à 1 alors la suite 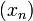converge vers zéro et même la série de terme général 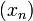est absolument convergente.
Donc, dans ce cas, si E est complet (par exemple si E=C), la série est convergente.
- si p est strictement supérieur à 1, alors la suite ne tend pas vers 0, donc la série diverge grossièrement.
- si p vaut 1, on ne peut pas conclure : c'est le cas douteux de la règle de Cauchy
Il faut prendre garde aux deux faits suivants:
- cette limite n'existe pas forcément
- la règle n'a pas de réciproque: la série de terme général 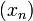peut être absolument convergente sans que la suite de terme général
![\sqrt[n] {\left\|x_n\right\|}](/pictures/frwiki/97/adc1b8563f0a6c992b519b209240e541.png)
ne soit convergente; tout ce qu'on peut dire est que si elle est convergente, alors sa limite ne peut être strictement supérieure à 1 et est donc inférieure ou égale à 1.
Énoncé plus précis
On retrouve le même énoncé en remplaçant la notion de limite par celle de limite supérieure dans la définition de p.
Voir aussi
Portail des mathématiques
Catégorie : Série
![p=\lim_{n \to +\infty}\sqrt[n] {\left\|x_n\right\|}](/pictures/frwiki/50/2607b93cbcac35dee47f0b2a033d53e7.png)
Wikimedia Foundation. 2010.
