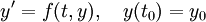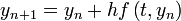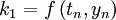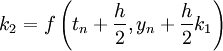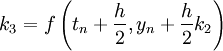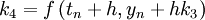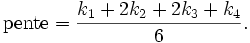Methodes de Runge-Kutta

Methodes de Runge-Kutta

Méthodes de Runge-Kutta

Les méthodes de Runge-Kutta sont des méthodes d'analyse numérique d'approximation de solutions d'équations différentielles. Elles ont été nommées ainsi en l'honneur des mathématiciens Carl Runge et Martin Wilhelm Kutta lesquels élaborèrent la méthode en 1901.

Ces méthodes reposent sur le principe de l'itération, c'est-à-dire qu'une première estimation de la solution est utilisée pour calculer une seconde estimation, plus précise, et ainsi de suite.

La méthode de Runge-Kutta d'ordre 1 (RK1)

Cette méthode est équivalente à la méthode d'Euler, une méthode simple de résolution d'équations différentielles du 1er degré.

Considérons le problème suivant :

y' = f(t, y), \quad y(t_0) = y_0

La méthode RK1 est donnée par l'équation

y_{n+1} = y_n + h f \left( t, y_n \right)

où h est le pas de l'itération.

La méthode de Runge-Kutta classique d'ordre quatre (RK4)

C'est un cas particulier d'usage très fréquent, dénoté RK4.

Considérons le problème suivant :

y' = f(t, y), \quad y(t_0) = y_0

La méthode RK4 est donnée par l'équation :

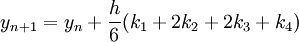
y_{n+1} = y_n + {h \over 6} (k_1 + 2k_2 + 2k_3 + k_4)

où

k_1 = f \left( t_n, y_n \right)
k_2 = f \left( t_n + {h \over 2}, y_n + {h\over 2} k_1 \right)
k_3 = f \left( t_n + {h \over 2}, y_n + {h\over 2} k_2 \right)
k_4 = f \left( t_n + h, y_n + h k_3\right)

L'idée est que la valeur suivante (yn+1) est approchée par la somme de la valeur actuelle (yn) et du produit de la taille de l'intervalle (h) par la pente estimée. La pente est obtenue par une moyenne pondérée de pentes :

  • k1 est la pente au début de l'intervalle ;
  • k2 est la pente au milieu de l'intervalle, en utilisant la pente k1 pour calculer la valeur de y au point tn + h/2 par le biais de la méthode d'Euler ;
  • k3 est de nouveau la pente au milieu de l'intervalle, mais obtenue cette fois en utilisant la pente k2 pour calculer y;
  • k4 est la pente à la fin de l'intervalle, avec la valeur de y calculée en utilisant k3.

Dans la moyenne des quatre pentes, un poids plus grand est donné aux pentes au point milieu.

\mbox{pente} = \frac{k_1 + 2k_2 + 2k_3 + k_4}{6}.

La méthode RK4 est une méthode d'ordre 4, ce qui signifie que l'erreur commise à chaque étape est de l'ordre de h5, alors que l'erreur totale accumulée est de l'ordre de h4.

Ces formules sont aussi valables pour des fonctions à valeurs vectorielles.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « M%C3%A9thodes de Runge-Kutta ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Methodes de Runge-Kutta de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Méthodes De Runge-Kutta — Les méthodes de Runge Kutta sont des méthodes d analyse numérique d approximation de solutions d équations différentielles. Elles ont été nommées ainsi en l honneur des mathématiciens Carl Runge et Martin Wilhelm Kutta lesquels élaborèrent la… …   Wikipédia en Français

  • Méthodes de runge-kutta — Les méthodes de Runge Kutta sont des méthodes d analyse numérique d approximation de solutions d équations différentielles. Elles ont été nommées ainsi en l honneur des mathématiciens Carl Runge et Martin Wilhelm Kutta lesquels élaborèrent la… …   Wikipédia en Français

  • Méthodes de Runge-Kutta — Les méthodes de Runge Kutta sont des méthodes d analyse numérique d approximation de solutions d équations différentielles. Elles ont été nommées ainsi en l honneur des mathématiciens Carl Runge et Martin Wilhelm Kutta lesquels élaborèrent la… …   Wikipédia en Français

  • Runge-Kutta — Méthodes de Runge Kutta Les méthodes de Runge Kutta sont des méthodes d analyse numérique d approximation de solutions d équations différentielles. Elles ont été nommées ainsi en l honneur des mathématiciens Carl Runge et Martin Wilhelm Kutta… …   Wikipédia en Français

  • Méthode de Runge-Kutta — Méthodes de Runge Kutta Les méthodes de Runge Kutta sont des méthodes d analyse numérique d approximation de solutions d équations différentielles. Elles ont été nommées ainsi en l honneur des mathématiciens Carl Runge et Martin Wilhelm Kutta… …   Wikipédia en Français

  • Carl Runge — Carl David Tolmé Runge, né le 30 août 1856 et mort le 3 janvier 1927, fut un mathématicien et physicien allemand. Il a co développé avec Martin Wilhelm Kutta une des méthodes de résolution numérique pour les équations… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Equation differentielle — Équation différentielle En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de différenciation auquel une… …   Wikipédia en Français

  • Equation différentielle — Équation différentielle En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de différenciation auquel une… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”