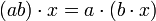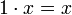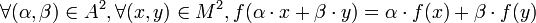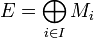- Théorie des modules
-
Module sur un anneau
Un module sur un anneau unitaire est une structure algébrique qui généralise celle d'espace vectoriel et celle d'idéal d'un anneau.
Dans un espace vectoriel l'ensemble des scalaires forme un corps tandis que dans un module, ceux-ci sont de manière plus générale munis d'une structure d'anneau (non nécessairement commutatif). Une partie des travaux en théorie des modules consiste à retrouver les résultats spectaculaires de la théorie des espaces vectoriels, quitte pour cela à travailler avec des anneaux plus maniables, comme les anneaux principaux.
Certaines propriétés vraies pour les espaces vectoriels ne sont plus vraies pour les modules. Par exemple l'existence d'une base n'y est plus assurée, et on ne peut pas nécessairement y développer de théorie de la dimension, même dans un module engendré par un nombre fini d'éléments.
Les modules ne sont pas une généralisation inutile. Ils apparaissent naturellement dans beaucoup de situations algébriques ou géométriques. Un exemple simple est un module sur l'anneau des fonctions infiniment différentiables sur un ouvert : il est naturel de ne pas pouvoir y faire de division, puisqu'il vaut mieux éviter de diviser par 0. De la même façon, il est naturel de considérer un module sur l'anneau des polynômes à une ou plusieurs variables.
Sommaire
Définitions
Module à gauche, module à droite
Si A est un anneau (unitaire), et (M , +) un groupe commutatif.
Si de plus, M est muni d'une loi externe
 de A × M dans M vérifiant, pour tous éléments a et b de A et x, y de M :
de A × M dans M vérifiant, pour tous éléments a et b de A et x, y de M :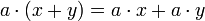 (distributivité de
(distributivité de  par rapport à l'addition dans M)
par rapport à l'addition dans M)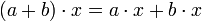 (distributivité de
(distributivité de  par rapport à l'addition dans A)
par rapport à l'addition dans A)
- Remarque : la loi + du membre de gauche est celle de l'anneau A et la loi + du membre de droite est celle du groupe M
alors (M, + ,
 ) est un A-module à gauche.
) est un A-module à gauche.Ce qui a été défini ici est un A-module à gauche, car, dans la loi externe, les éléments de A sont placés à gauche. On pourra définir de même un A-module à droite.
Il est important de remarquer que les structures de module à gauche et à droite ne diffèrent pas uniquement par leur écriture : si les deux premiers axiomes sont les mêmes, le troisième s'écrit
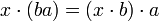 . Si l'on transcrivait naïvement cette égalité en écrivant les éléments de A gauche, on obtiendrait
. Si l'on transcrivait naïvement cette égalité en écrivant les éléments de A gauche, on obtiendrait 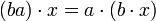 , ce qui, si A n'est pas commutatif, ne revient pas au même que l'axiome qui donne la structure de module à gauche.
, ce qui, si A n'est pas commutatif, ne revient pas au même que l'axiome qui donne la structure de module à gauche.Par contre, le petit raisonnement ci-dessus montre que, si l'on "inverse" la loi de A, un module à droite peut être vu comme un module à gauche. Plus précisément, notons Aop l'anneau "opposé" à A, c'est-à-dire le groupe abélien A muni de la multiplication définie par aopbop = ba, si aop et bop désignent a et b vus comme éléments de Aop. Alors, si M est un A-module à gauche, M peut être vu comme un Aop-module à droite, où l'action de Aop est définie par a.m = m.aop.
Ceci justifie que dans la suite, on puisse se restreindre à l'étude des modules à gauche.
Notons que la condition d'exoneutralité :
 peut sembler superflue ou évidente. Il n'en est rien. On peut en effet trouver un modèle de la théorie des modules (à gauche) dans lequel cette condition n'est pas satisfaite. Ceci prouve qu'elle ne se déduit pas des autres axiomes de la théorie. Et un tel modèle est en fait très facile à définir : il suffit de faire agir A sur A en posant, pour tous
peut sembler superflue ou évidente. Il n'en est rien. On peut en effet trouver un modèle de la théorie des modules (à gauche) dans lequel cette condition n'est pas satisfaite. Ceci prouve qu'elle ne se déduit pas des autres axiomes de la théorie. Et un tel modèle est en fait très facile à définir : il suffit de faire agir A sur A en posant, pour tous 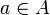 et
et 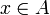 ,
, 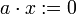 . Tous les axiomes sont satisfaits sauf l'exoneutralité puisque pour tout
. Tous les axiomes sont satisfaits sauf l'exoneutralité puisque pour tout 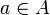 ,
, 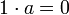 .
.Exemples
- Lorsque A est un corps, on retrouve la structure habituelle de A-espace vectoriel. Dans ce cas, les éléments de A sont appelés les scalaires, les éléments de M sont appelés les vecteurs.
- A lui-même est à la fois un module à gauche et à droite.
- L'ensemble des vecteurs du plan dont les coordonnées sont des entiers relatifs forme un
 -module.
-module. - Tout groupe abélien est automatiquement un
 -module pour la loi externe définie par :
-module pour la loi externe définie par :
-
- pour n > 0,
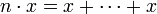 avec n termes x
avec n termes x - pour n = 0
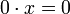
- pour n < 0,
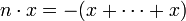 avec |n| termes x
avec |n| termes x
- pour n > 0,
Cette loi est la seule qui munisse un groupe abélien d'une structure de
 -module. Il y a donc équivalence entre la notion de
-module. Il y a donc équivalence entre la notion de  -module et celle de groupe abélien.
-module et celle de groupe abélien.- La structure de A-module apparaît dans celle d'algèbre sur un anneau.
- Si M un groupe abélien et si f est un endomorphisme de groupe sur M, alors on peut définir la loi externe
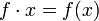 qui confère à M une structure de End(M)-module .
qui confère à M une structure de End(M)-module . - Si M est un espace vectoriel, on peut faire la même chose avec des endomorphismes d'espaces vectoriels au lieu de groupes. Par exemple, l'espace vectoriel
 à n dimensions est un module à gauche sur
à n dimensions est un module à gauche sur 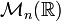 via la multiplication matricielle.
via la multiplication matricielle. - Si M est un A-module à gauche, l'ensemble des applications d'un ensemble S vers M est un A-module à gauche, pour les lois (f + g)(x) = f(x) + g(x) et
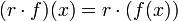
- Un espace vectoriel
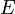 sur un corps
sur un corps  peut être considéré comme un module sur l'anneau principal
peut être considéré comme un module sur l'anneau principal ![\mathbb K[X]](/pictures/frwiki/49/11cf18672fa8c102e5d2ec8bdfe203c8.png) , et par ce biais la majeure partie des propriétés de l'algèbre linéaire peut être démontrée[1].
, et par ce biais la majeure partie des propriétés de l'algèbre linéaire peut être démontrée[1].
Cette structure de module est la suivante : étant donné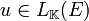 fixé, pour tout
fixé, pour tout ![\left( p, x \right) \in \mathbb K[X]\times E](/pictures/frwiki/52/4fe3999552e4b77d3dcb48d887246383.png) , on pose
, on pose 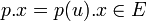 , avec
, avec 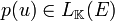 car cet ensemble a une structure d'algèbre sur
car cet ensemble a une structure d'algèbre sur  .
.
Lien avec la théorie de la représentation
Le premier axiome montre que, pour
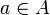 , l'application
, l'application 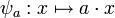 est un endomorphisme du groupe M. Les trois axiomes suivants traduisent quant à eux le fait que l'application
est un endomorphisme du groupe M. Les trois axiomes suivants traduisent quant à eux le fait que l'application 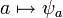 est un morphisme (unitaire) de l'anneau A dans l'anneau des endomorphismes de M, noté End(M).
est un morphisme (unitaire) de l'anneau A dans l'anneau des endomorphismes de M, noté End(M).Réciproquement, la donnée d'un morphisme d'anneau unitaire
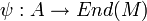 fournit à M une structure de A-module (à gauche) via la loi
fournit à M une structure de A-module (à gauche) via la loi 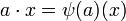 . Une structure de A-module est donc équivalente à la donnée d'un morphisme
. Une structure de A-module est donc équivalente à la donnée d'un morphisme 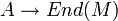 .
.Un tel morphisme A
 End(M) est appelé une représentation de A sur le groupe abélien M. Une représentation est dite fidèle si elle est injective. En termes de module, cela signifie que si pour tout
End(M) est appelé une représentation de A sur le groupe abélien M. Une représentation est dite fidèle si elle est injective. En termes de module, cela signifie que si pour tout 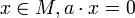 , alors a = 0.
, alors a = 0.Ceci est une généralisation de ce que l'on trouve en représentation des groupes, où l'on définit une représentation d'un groupe G vers un espace vectoriel sur un corps K comme un morphisme de l'algèbre du groupe K[G] vers End(V), autrement dit, où l'on donne une structure de K[G]-module à V.
Sous-module
Soit E un A-module à gauche, et M une partie de E. On dit que M est un sous-module (à gauche) si les conditions suivantes sont respectées :
- M est un sous-groupe de (E,+)
- Pour tout
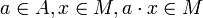
Autrement dit, un sous-module est une partie linéairement stable.
Exemples
- Un cas très important est celui des sous-modules de A en tant A-module : ils ne sont autres que les idéaux à gauche ou à droite selon le type de module choisi, de l'anneau A.
- Si le module est un espace vectoriel, on parle de sous-espace vectoriel
- Dans un groupe commutatif, considéré comme module sur
 , tout sous-groupe est aussi un sous-module.
, tout sous-groupe est aussi un sous-module.
Applications linéaires
Une application linéaire f entre deux modules M et N sur un même anneau A est une fonction qui conserve la structure de module, i.e qui vérifie :
Autrement dit, une application linéaire est un morphisme de modules. Si f est bijective, on dit de plus que f est un isomorphisme. Si les modules de départ et d'arrivée M et N sont identiques, on dit que f est un endomorphisme. Si f est à la fois un endomorphisme et un isomorphisme, on dit que c'est un automorphisme.
Le noyau d'une application linéaire f est l'ensemble des éléments x de M qui vérifient f(x) = 0. C'est un sous-module de M et il est noté Ker f. On peut également définir l'image d'une application linéaire Im f = f(M) qui est un sous-module de N.
Comme dans le cas des groupes ou des anneaux, un morphisme de A-modules
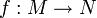 donne lieu à un isomorphisme
donne lieu à un isomorphisme 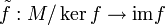 , défini par
, défini par 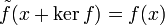
Opérations sur les modules
Produits de modules
Si on considère une famille de module (
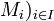 sur un même anneau A, on peut munir l'ensemble produit
sur un même anneau A, on peut munir l'ensemble produit 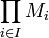 d'une structure de module en définissant les lois suivantes :
d'une structure de module en définissant les lois suivantes :- Loi interne :
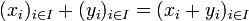
- Loi externe :
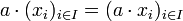
Le module ainsi défini s'appelle le module produit. Les projections
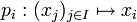 sont alors des applications linéaires surjectives. Un exemple important de produit de modules est celui où tous les modules facteurs sont identiques à un même module M ; leur produit MI n'est alors autre que l'ensemble des applications de I dans M.
sont alors des applications linéaires surjectives. Un exemple important de produit de modules est celui où tous les modules facteurs sont identiques à un même module M ; leur produit MI n'est alors autre que l'ensemble des applications de I dans M.Somme directe de modules
Soit
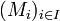 une famille de A-modules, on note leur produit
une famille de A-modules, on note leur produit 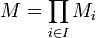 . L'ensemble E des éléments de M dont toutes les composantes sauf un nombre fini sont nulles est appelé somme directe externe de la famille de modules
. L'ensemble E des éléments de M dont toutes les composantes sauf un nombre fini sont nulles est appelé somme directe externe de la famille de modules 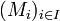 et il est noté :
et il est noté :C'est un sous-module de
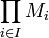 . Dans le cas où I est fini, la somme directe E et le produit M sont évidemment confondus.
. Dans le cas où I est fini, la somme directe E et le produit M sont évidemment confondus.Intersection et somme de sous-modules
Si M est un module, et
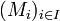 est une collection de sous-modules de M, on dit que la famille est en somme directe si :
est une collection de sous-modules de M, on dit que la famille est en somme directe si :-
- Pour toute partie J finie de I, pour tout
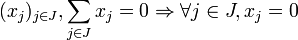
- Pour toute partie J finie de I, pour tout
Dans ce cas, la somme
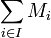 , appelée somme directe interne, est isomorphe à la somme directe externe et elle est également notée
, appelée somme directe interne, est isomorphe à la somme directe externe et elle est également notée 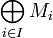 .
.Familles libres, bases
On dit qu'un A-module est de type fini s'il est engendré sur A par un nombre fini d'éléments. On a alors
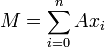 .
.On dit qu'un A-module est libre s'il possède une base sur A.
Si M est de type fini et libre, il existe alors un isomorphisme entre M et An, où n est le cardinal de la base.
A quoi servent les modules
Les modules sont un outil indispensable pour passer de propriétés géométriques à des propriétés fonctionnelles, ou ressemblant à des propriétés fonctionnelles. Ainsi, au lieu de voir une variété différentiable comme une partie d'un espace concret ou abstrait, on va plutôt considérer une classe de fonctions sur cette variété et déclarer que cette classe est la classe des fonctions différentiables sur la variété -- il faudra satisfaire des conditions appropriées de compatibilité. On pourra ainsi traduire les propriétés géométriques de la variété par des propriétés algébriques de la classe de fonctions que nous avons déclarées comme fonctions différentiables.
Mieux que des fonctions, on peut considérer des champs sur une variété différentiable. Le cas le plus simple est celui des champs tangents différentiables à une variété. Pensons par exemple aux champs de vecteurs tangents à la sphère unité dans un espace de dimension 3. Il s'agit bien d'un module sur l'anneau des fonctions différentiables sur la sphère : si on multiplie un champ différentiable tangent à la sphère par une fonction différentiable, on trouve bien un champ différentiable. Ce module est engendré par la restriction à la sphère des projections tangentes des champs constants égaux aux vecteurs de base de l'espace - cela nous fait trois champs. Mais on peut montrer que ces trois champs ne sont pas indépendants, et on peut même montrer qu'il n'existe aucun choix de deux champs tangents qui pourraient engendrer le module des champs tangents à la sphère et différentiables. On a là l'exemple le plus simple d'un module de type fini, c'est à dire engendré par un nombre fini de ses éléments, mais qui ne possède pas de base.
La correspondance systématique entre objet géométrique et objet de nature fonctionnelle est dominante en géométrie algébrique. En effet, si V est l'ensemble des solutions communes d'un système d'équations polynomiales en n variables, on peut étudier l'ensemble des polynômes qui s'annulent sur V; ce sera un idéal de l'anneau des polynômes à n variables, et donc en particulier, un module sur cet anneau. Il est possible de retrouver nombre de propriétés géométrique de V en étudiant les propriétés de cet idéal: points singuliers, dimension, recherche de droites incluses dans V, et ainsi de suite.
Cette faculté d'exprimer les propriétés d'objets géométriques au moyen d'espaces de fonctions sur ces objets est à la base de la géométrie non commutative: les espaces de fonctions sur des objets géométriques usuels sont des anneaux commutatifs pour la multiplication (et même souvent des algèbres, c'est à dire des anneaux munis également d'une structure compatible d'espace vectoriel). La démarche de la géométrie non commutative consiste à explorer ce que seraient des objets géométriques sur lesquels vivraient des "fonctions" formant un anneau ou une algèbre non commutative, et c'est pour cette raison que le cas des anneaux non commutatifs et des modules sur des anneaux non commutatifs est très important actuellement.
Voir aussi
- produit tensoriel de deux modules
- multimodule
- longueur d'un module
- dual d'un module
- module projectif
- facteur invariant
Notes et références
- ↑ Algèbre Agrégation, Licence 3e année, de Patrice Tauvel, Dunod éditeur, 2005, ISBN 2100494120, ISBN 978-2100494125.
- Portail des mathématiques
Catégorie : Structure externe
Wikimedia Foundation. 2010.