Anneau Principal

Anneau Principal

Anneau principal

Les anneaux principaux forment un type d'anneaux important dans la théorie mathématique de la divisibilité. Ce sont les anneaux intègres (commutatifs unitaires non nuls) auxquels on peut étendre deux théorèmes qui, au sens strict, concernent l'anneau des entiers relatifs : le théorème de Bachet-Bézout et le théorème fondamental de l'arithmétique.

Sommaire

Définitions

Un anneau A est dit unitaire s'il admet un élément neutre pour la multiplication. Il est dit intègre si pour tous éléments a et b de A tels que a.b soit égal à zéro, un au moins des éléments a et b est nul. Cette propriété a pour conséquence que tout élément non nul de A est simplifiable, c'est-à-dire que si a est un élément non nul de A, si b et c sont deux éléments de A tels que a.b = a.c (resp. b.a = c.a), alors b est égal à c. La simplification utilisée pour les calculs sur les nombres entiers, rationnels, réels ou complexe est donc toujours valable. Enfin l'anneau A est dit commutatif si, pour tous éléments a et b de A, a.b = b.a. Dans toute la suite de l'article, A désigne un anneau commutatif unitaire intègre.

Un idéal J est un sous-groupe de A stable par multiplication de n'importe quel élément a de A, ainsi si j est élément de J, a.j l'est aussi, ou encore a.J est inclus dans J. L'idéal J est dit principal s'il est composé des multiples d'un élément de l'anneau.

  • Un idéal J de l'anneau A est dit principal si et seulement s'il existe un élément a de A tel que J est égal à a.A.
  • Un anneau commutatif unitaire et intègre est dit principal si et seulement si tous ses idéaux sont principaux.[1]

Exemples et contre exemples

Corps

Article détaillé : Corps (mathématiques).

Les corps sont des anneaux principaux. En effet, les deux seuls idéaux sont les idéaux triviaux engendrés par les éléments neutres de l'addition, qui correspond à l'idéal réduit à un élément, ainsi que celle de la multiplication, qui correspond à l'anneau entier. En revanche, l'étude d'une telle structure n'utilise pas cette propriété, car les seuls idéaux sont triviaux.

Pour les anneaux finis, les seuls anneaux intègres sont les corps. En effet, si l'anneau A est fini et si a est un élément non nul de A, alors l'application de A dans A qui à x associe a.x est injective. Une application injective d'un ensemble de cardinal fini dans lui-même est surjective, il existe donc un élément b tel que a.b = 1. Comme l'anneau est commutatif, a.b = b.a = 1, ce qui montre que a est inversible et donc que A est un corps.

Anneau euclidien

Article détaillé : Anneau euclidien.

Un anneau euclidien est un anneau disposant d'une division euclidienne. Un tel anneau est toujours principal (cf l'article détaillé). Des exemples de cette nature sont donnés par Z, l'ensemble des entiers relatifs ou encore l'ensemble des polynômes à coefficients dans un corps, par exemple celui des rationnels, réels ou complexes.

Tous les anneaux principaux ne sont pas euclidiens :

  • Soit ω le nombre complexe défini par ω = 1/2 (1 + i√19), où i désigne l'unité imaginaire, le plus petit anneau unitaire Z[ω] du corps des nombres complexes contenant ω est principal mais n'est pas euclidien.[2]
Démonstration
  • L'anneau Z[ω] est principal :

L'analyse du groupe des classes d'idéaux montre que s'il existe des idéaux non principaux de Z[ω], alors il en existe un de norme inférieure ou égal à 2.√19 / π (cf l'article Entier quadratique). La norme d'un idéal J est égal au cardinal de l'anneau Z[ω] / J. Comme 2.√19 / π est inférieur à 2,8, il suffit de montrer qu'il n'existe aucun idéal J tel que Z[ω] / J soit isomorphe à Z/2Z.

Soit J un idéal de norme deux, le morphisme canonique de Z[ω] dans Z[ω] / J induit un morphisme φ de Z[ω] dans Z/2Z. Tout idéal de norme égale à deux est le noyau d'un tel morphisme. Déterminons l'image de ω par φ. On remarque que ω2 - ω + 5 est égal à 0. On en déduit :

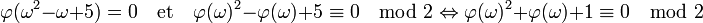
\varphi (\omega^2 - \omega + 5) = 0 \quad \text{et}\quad \varphi (\omega)^2 - \varphi (\omega) + 5 \equiv 0 \mod 2 \Leftrightarrow \varphi (\omega)^2 + \varphi (\omega) + 1 \equiv 0 \mod 2

Or dans Z/2Z le polynôme X2 + X + 1 est irréductible, c'est-à-dire qu'il n'admet pas de racine. Il n'existe donc pas d'idéal de Z[ω] de norme égale à deux. S'il existait dans Z[ω] un idéal non principal, alors il existerait un idéal non principal de norme égal à deux. Or, il n'existe aucun idéal de norme égal à deux, ce qui montre que l'anneau Z[ω] est principal.

Le groupe des unités d'un anneau unitaire désigne l'ensemble des éléments inversibles, encore appelés unités, de l'anneau. Cet ensemble forme un groupe pour la multiplication. Soit z un élément non nul de Z[ω], il existe deux entiers relatifs a et b tel que z = a + b.ω (cf l'article Entier quadratique). Le carré du module de z est un entier strictement positif égal à a2 + a.b + 5b2. Si z−1 est élément de Z[ω] alors son module est un entier strictement positif et comme le produit des modules de z et z−1 est égal à 1 et que le carré du module de z−1 est égal à l'inverse du carré du module de z, le module de z est nécessairement égal à un. La valeur de b est donc égal à zéro et celle de a à un en valeur absolue, ce qui montre la proposition.

  • Il n'existe pas d'idéal non nul J tel que Z[ω] / J contienne strictement moins que quatre éléments :

On a déjà démontré que si J est un idéal non nul de Z[ω], Z[ω] / J n'est pas de cardinal deux, il suffit donc de démontrer que le quotient ne peut contenir trois éléments. Le raisonnement précédent montre qu'un tel quotient n'existe que si le polynôme P[X] suivant dans Z / 3Z admet une racine :

P[X] = X^2 - X + 5 \mod 3 \Leftrightarrow P[X] = X^2 + 2X + 2 = (X + 1)^2 + 1 \mod 3 \;

Dans Z / 3Z les seuls carrés sont zéro et un, le polynôme P[X] est irréductible dans Z / 3Z et il n'existe pas de morphisme autre que trivial de Z[ω] dans Z / 3Z. Ceci montre qu'il n'existe pas d'idéal J tel que Z[ω] / J contienne exactement trois éléments et termine la démonstration.

  • L'anneau Z[ω] n'est pas euclidien :

Raisonnons par l'absurde, soit δ un stathme euclidien sur Z[ω] - {0}. Il est toujours possible de choisir δ tel que son image soit égal à un pour un élément z de Z[ω] si et seulement si z est inversible. Le stathme ne peut être constant égal à un sur Z[ω] car si tel était le cas, Z[ω] serait un corps (tout élément non nul est inversible), or deux n'est pas inversible dans Z[ω].

Soit z un élément de Z[ω] tel que δ(z) soit la plus petite valeur strictement supérieure à un et atteinte par le stathme. Le reste de la division euclidienne d'un élément quelconque de Z[ω] par z est, soit nulle, soit un élément du groupe des unités. Le quotient Z[ω] / zZ[ω] contient au plus trois éléments : la classe de zéro ou une classe d'un élément du groupe des unités. Comme le seul idéal J de Z[ω] tel que Z[ω] / J contienne strictement moins de quatre éléments est l'idéal trivial {0}, z est donc inversible. La contradiction réside dans le fait que z est un élément inversible tel que δ(z) est strictement supérieur à un. Cette impossibilité termine la démonstration.

 

Anneau d'entiers

Article détaillé : Entier quadratique.

Un corps de nombres K est un sous-corps de C, l'ensemble des complexes, de dimension finie en tant qu'espace vectoriel sur Q l'ensemble des rationnels. Sa fermeture intégrale est l'ensemble des éléments de K admettant un polynôme minimal à coefficients dans Z, l'anneau des entiers relatifs. Un tel ensemble forme un anneau.

Si le corps est quadratique, c'est-à-dire si tout élément s'exprime comme la combinaison linéaire sur Q de 1 et d'une racine carré d'un nombre rationnel sans facteur carré, l'anneau associé peut être principal. C'est le cas par exemple pour les entiers de Gauss, d'Eisenstein ou de Dirichlet.

Les anneaux principaux de cette nature sont relativement rares. Ceux qui ne sont pas inclus dans R, l'ensemble des réels, sont tous connus. Ce résultat fait l'objet d'un théorème dit de Stark-Heegner. La question de savoir s'il existe une infinité de corps quadratiques réels dont l'anneau des entiers soit principal est encore ouverte (c'est-à-dire que la réponse n'est pas connue).

En théorie des nombres, un autre type d'anneau principal est l'anneau à valuation discrète. Ce type d'anneau est un cas particulier d'anneau local, c'est-à-dire d'anneau n'ayant qu'un unique idéal premier. Si un anneau d'entiers algébriques est de Dedekind alors l' anneau localisé d'un idéal premier est local et principal.

Exemple issu de l'analyse

Les anneaux principaux ne se trouvent pas uniquement en algèbre, l'exemple suivant[3] est utilisé en analyse complexe :

  • Soit X un espace compact de C (l'ensemble des complexes) et A l'anneau des fonctions holomorphes de X dans C, (c'est-à-dire qui sont holomorphes sur un voisinage ouvert de X), l'anneau A est principal.
Démonstration

Soit J un idéal de A, et (fi) pour i élément de I une famille génératrice de l'idéal J, composée de fonctions non nulles. La fonction fi est holomorphe et n'admet qu'un nombre fini de racines à un ordre de multiplicité finie. Il existe donc un polynôme pi tel que le quotient fi / pi soit une fonction de A qui ne s'annule pas sur X. Le quotient est une unité, ce qui montre que la famille de polynômes (pi) est génératrice de l'idéal J.

Soit M l'idéal de l'ensemble des polynômes à coefficients dans C engendré par la famille (pi). Cet idéal est principal car l'anneau des polynômes à coefficients dans C l'est. Soit m un polynôme engendrant M. Par définition m est élément de M et donc élément de J. Par construction m engendre pi et donc fi. L'idéal engendré par m contient donc J et est contenu dans J, ce qui démontre que J est principal.

 

Contre-exemples

Les anneaux commutatifs unitaires intègres non principaux sont nombreux.

Une première famille de contre-exemples est fournie par les anneaux de polynômes. Si A n'est pas un corps A[X] n'est pas un anneau principal (cf l'article Anneau euclidien). En effet, si a est un élément non inversible de A, l'idéal des polynômes ayant pour constante un multiple de a n'est pas principal. L'anneau des polynômes A[X, Y] n'est jamais principal, même si A est un corps. Il suffit pour s'en rendre compte de considérer le plus petit idéal contenant les polynômes X et Y, un tel idéal n'est pas principal.

Les entiers algébriques fournissent des anneaux non principaux. L'anneau Z[i√5] est un contre exemple étudié dans l'article Entier quadratique.

Propriétés

Arithmétique

L'arithmétique élémentaire sur l'anneau des entiers relatifs se fonde sur quelques théorèmes clé. A l'exception de la division euclidienne qui n'est pas définie dans le cas général d'un anneau principal, ces grands théorèmes s'appliquent encore dans ce contexte. Ces théorème permettent de généraliser les raisonnements arithmétiques à tous les anneaux principaux.

Le théorème de Bachet-Bézout est encore vérifié :

  • Si a et b sont deux éléments de A n'ayant pas d'autres diviseurs communs que les éléments du groupe des unités de l'anneau, alors il existe u et v éléments du groupe tel que a.u + b.v = 1.

Cette propriété résulte du fait que l'idéal engendré par a et b est principal, et tout générateur de cet idéal est diviseur commun à a et b, donc est inversible et engendre l'anneau tout entier. En particulier, l'élément 1 appartient à cet idéal, ce qui entraîne la relation.

Une fois établies les définitions de pgcd et ppcm, l'identité de Bézout prend une forme un peu différente : l'équation diophantienne ax+by = c admet des solutions si et seulement si c est un multiple du pgcd de a et de b.

Le lemme d'Euclide aussi est vérifié :

  • Soit a, b et c trois éléments de A tel que a divise b.c et tel qu'il n'existe pas d'autres diviseurs commun à a et à b que les éléments du groupe des unités. Alors a est un diviseur de c.

En effet, l'identité de Bézout assure l'existence de deux éléments de A, u et v tel que a.u + b.v = 1. La multiplication par c des deux membres de cette égalité permet d'écrire (i) a.u.c + b.c.v = c. De plus, a est un diviseur de b.c, ce qui se traduit par l'existence d'un élément d de A tel que: (ii) b.c = a.d. Les égalités (i) et (ii) démontre l'égalité suivante: a.( u.c + v.d) = c. Ceci montre que a divise c et le lemme d'Euclide est bien vérifié.

Enfin, le théorème fondamental de l'arithmétique est vérifié :

  • Un anneau principal est anneau factoriel, c'est-à-dire que tout élément de l'anneau de décompose de manière unique (aux facteurs inversibles près) en un produit de facteurs irréductibles.

Une unité désigne un élément qui possède un inverse dans l'anneau. Un facteur irréductible de l'anneau est un élément p tel que chacune de ses décompositions en produit de deux facteurs contienne au moins une unité. Ainsi dans Z, -2 est irréductible car toute décomposition en un produit de deux facteurs contient nécessairement 1 ou -1 comme facteur. La décomposition est unique à un facteur inversible près. On remarque en effet qu'il existe plusieurs décompositions, par exemple de 6, 6 = 2 x 3 = (-2) x (-3). En revanche, ces deux décompositions sont les mêmes, à un facteur inversible près. Une démonstration est présentée dans l'article Anneau factoriel.

Idéal

  • Un élément a est premier si et seulement si A/a.A est un corps.

Soit b un élément dont la classe dans l’anneau quotient est non nulle, alors b n'est pas élément de a.A. Comme a est premier, il n'existe pas d'autres diviseurs communs que les éléments du groupe des unités. L'identité de Bézout, par passage aux classes montre que b est inversible. L'idéal a.A est dit maximal, c'est-à-dire que les seuls idéaux contenant a.A sont lui-même et A tout entier.

Réciproquement si A/a.A est un corps, soit b un diviseur de a qui ne soit pas un élément inversible, alors il existe un élément c de l'anneau tel que b.c = a et la classe de b est un diviseur de zéro. Le seul diviseur de zéro d'un corps est zéro. Ceci montre que b est dans l'idéal a.A et b est un multiple de a. L'élément b est à la fois un diviseur et un multiple de a, ceci montre que c est inversible. Ainsi, tout diviseur de a non inversible est égal à a, à un facteur inversible près, ce qui démontre que a est premier.

On remarque que si a est premier l'idéal est aussi premier, on en déduit la proposition :

  • Les idéaux premiers de A sont les idéaux maximaux.

Propriétés noethériennes

Article détaillé : anneau noethérien.

Un anneau principal est noethérien, c'est-à-dire qu'il vérifie la propriété suivante :

  • Toute suite (Jn) d'idéaux croissante est stable à partir d'un certain rang.

En effet, l'union J de tous les idéaux de la suite (Jn) est un idéal car la suite est emboitée. Soit a un générateur de J, il existe une valeur μ tel que Jμ contient a. On en déduit les inclusions suivantes :

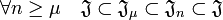
\forall n \ge \mu \quad \mathfrak J \subset \mathfrak J_{\mu} \subset \mathfrak J_n \subset \mathfrak J

Ces inclusions montrent qu'à partir du rang μ, la suite est stationnaire égale à Jμ.

La dernière propriété possède quelques corollaires, les deux suivants sont vrais pour tous les anneaux, mais impose l'usage d'une forme plus élaborée de l'axiome du choix pour une démonstration du cas général :

  • Tout idéal distinct de l'anneau est inclus dans un idéal maximal.

En effet, si un idéal n'est pas inclus dans un idéal maximal, il est possible de construire une suite croissante qui n'est jamais stationnaire et l'anneau n'est pas principal.

  • Un élément de A est inversible si et seulement s'il n'est inclus dans aucun idéal maximal.

Soit u un élément inversible, l'unique idéal contenant u contient l'anneau A tout entier, u n'est en conséquence pas inclus dans un idéal maximal.

Réciproquement soit a un élément de A non inversible, la proposition précédente montre que a.A est inclus dans un idéal maximal, ce qui permet de conclure.

Anneau de Dedekind

Article détaillé : Anneau de Dedekind.

Il existe un cas particulier d'anneau noethérien important en théorie des nombres, l'anneau de Dedekind. Un anneau A de Dedekind est un anneau commutatif unitaire intègre et noethérien tel que tout idéal premier est maximal et tel que la clôture algébrique de A est égal à l'anneau lui-même. Comme A est un anneau commutatif unitaire intègre il est possible de construire son corps des fractions K. Un élément de K est dit entier sur A si et seulement si son polynôme minimal est à coefficient dans A. l'ensemble des entiers de K sur A forme un anneau B. Si A est principal alors B est égal à A et on dit que A est intégralement clos[4]. Un anneau commutatif unitaire intègre est dit de Dedekind s'il est noethérien, si tout idéal premier est maximal et si l'anneau est intégralement clos.

  • Un anneau principal est intégralement clos.

On en déduit la proposition suivante :

  • Un anneau principal est de Dedekind.
Démonstration

Soient A un anneau principal, K son corps des fractions et α / β un entier de K sur A, avec α et β deux éléments de A premiers entre eux. Dire que α / β est entier revient à dire qu'il existe un entier naturel n et des éléments (ai) pour i variant de zéro à n - 1 tel que :

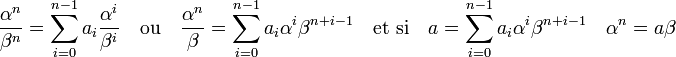
\frac {\alpha^n}{\beta^n} = \sum_{i=0}^{n-1} a_i \frac {\alpha^i}{\beta^i} \quad \text{ou}\quad \frac {\alpha^n}{\beta} = \sum_{i=0}^{n-1} a_i \alpha^i \beta^{n+i-1}\quad \text{et si}\quad a = \sum_{i=0}^{n-1} a_i \alpha^i \beta^{n+i-1}\quad \alpha^n = a\beta

L'élément β est premier avec α, il est donc premier avec αn. Comme β divise αn on en déduit que β est un élément inversible de A, ce qui montre que α / β est élément de A et par voie de conséquence tout entier de K sur A est un élément de A.

L'anneau A est intégralement clos, les démonstrations précédentes montrent que tout idéal premier est maximal et l'anneau est noethérien, il est donc de Dedekind.

 

Module sur un anneau principal

Un module sur un anneau est aux anneaux ce qu'un espace vectoriel est à un corps. Un module sur un anneau A commutatif unitaire et intègre est un groupe abélien disposant d'une multiplication externe dotée des mêmes propriétés que celle d'un espace vectoriel.

  • Un module est dit libre s'il admet une base. Il est dit de type fini s'il admet une famille génératrice de cardinal fini.

La situation n'est pas la même que celle d'un espace vectoriel. Un module de type fini n'admet pas nécessairement une base. Par exemple un groupe abélien fini G peut être aussi vu comme un Z module si z est un entier relatif et m un élément du module, z.m est égal à l'itérée m + m + ... + m z fois si z est positif et l'inverse de l'itéré -z fois si z est négatif. Toute famille finie (gi) de G admet une relation linéaire non triviale, si e est l'exposant du groupe G, e.g1 + e.g2 + ... est égal à zéro. Cette configuration est étudiée dans l'article groupe abélien de type fini.

Dans le cas d'un anneau principal A, la configuration est proche de celle des espaces vectoriels :

  • Soit M un A module libre de type fini et de rang m, tout sous A module N de M admet une base de cardinal inférieur ou égal à m.[5]

Une corollaire immédiat est le suivant :

  • Un module libre de type fini sur un anneau principal est noethérien.

Dans le cas d'un anneau euclidien, il existe un algorithme effectif permettant de déterminer une base. Il se trouve dans l'article Théorème des facteurs invariants.

Démonstration

Raisonnons par récurrence sur m.

Si m est égal à zéro, le résultat est immédiat.

Supposons la propriété démontrée pour m - 1 et démontrons là pour m. Soient (ei) pour i variant de un à m une base de M et P le module libre engendré par la base (ei) pour i variant de un à m - 1. L'intersection de N et de P est, par hypothèse de récurrence un module libre de rang inférieur ou égal à m - 1. Soit (fi) pour i variant de un à n - 1 une base de l'intersection de N et de P.

Notons J l'ensemble des coordonnées de em utilisée dans l'écriture des éléments de N dans la base (ei). L'ensemble J est un idéal de A, il existe donc un élément g de A, tel que l'idéal J soit engendré par g, notons fn un élément g.em + p de N, où p est un élément de P. Par définition de J, un tel élément existe.

Si g est égal à zéro, alors N est inclus dans P et l'hypothèse de récurrence permet de conclure. Sinon, montrons que (fi) pour i variant de un à n est une base de N. La famille est libre, en effet soit la combinaison linéaire nulle suivante :

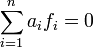
\sum_{i=1}^n a_if_i = 0 \;

Soit pr la projection de M sur P parallèlement à A.em. L'image de la combinaison linéaire par pr est égale à an g.em. Comme g n'est pas nul, an l'est. La combinaison linéaire précédente se réduit à celle de la famille libre (fi) pour i variant de un à n - 1. Comme cette famille est libre et la combinaison linéaire est nulle, les coefficients sont tous nuls. On en déduit que la famille des coefficients est nulle, ce qui montre que la famille est libre.

Montrons que la famille est génératrice. Soit v un élément de N, si v est inclus dans P alors il est combinaison linéaire de la famille (fi), qui engendre l'intersection de N et de P. Sinon, il existe un élément a de A tel que la mième coordonnée de v dans la base (ei) soit égal à a.g. On en déduit que v - a.fn est un élément de l'intersection de P et de N et ce vecteur est combinaison linéaire de la famille (fi). On en déduit que v est engendré par la famille (fi) qui est donc génératrice.

La famille est libre et génératrice, c'est une base de N, ce qui termine la démonstration.

 

Généralisations

Les anneaux principaux disposent de tous les théorèmes qui fondent l'arithmétique sur l'ensemble des entiers relatifs. En revanche, il existe de nombreux anneaux commutatifs unitaires et intègres qui ne sont pas principaux.

Géométrie algébrique

Article détaillé : Géométrie algébrique.

La géométrie algébrique étudie principalement les variétés algébriques, c'est-à-dire les hypersurfaces d'un espace vectoriel de dimension n sur un corps K définies comme les racines d'un idéal de l'anneau des polynômes à n indéterminées. Ainsi la sphère de R3 est définie comme les racines des polynômes à coefficients réels multiple de X2 + Y2 + Z2 - 1. Or l'anneau des polynômes à plusieurs variables n'est pas un anneau principal.

Un anneau factoriel est par définition un anneau où un analogue du théorème fondamental de l'arithmétique est vérifié. Le lemme d'Euclide est vrai dans un tel anneau, ce n'est en revanche pas le cas du théorème de Bezout, qui caractérise en fait les anneaux principaux parmi les anneaux factoriels. Les anneaux de polynômes en plusieurs indéterminées à coefficients dans un corps sont par exemple factoriels mais pas principaux.

Théorie algébrique des nombres

Article détaillé : Théorie algébrique des nombres.

La solution utilisée pour les anneaux de polynômes n'est pas toujours pertinente. Les anneaux d'entiers algébriques, par exemple, ne sont pas toujours factoriels. Une autre approche permet néanmoins de retrouver une arithmétique analogue.

Les anneaux d'entiers algébriques sur un corps de nombres c'est-à-dire des extensions finies des nombres rationnels possèdent des idéaux non principaux. En revanche, il suffit d'une famille finie d'éléments pour générer tout idéal. Plus précisément, tout idéal d'un anneau d'entiers algébriques sur un corps de nombre A est un sous-A module disposant d'une base de cardinal égal à la dimension du corps de nombres, considéré comme un Q espace vectoriel. Un anneau A qui ne possède que des idéaux de type fini (c'est-à-dire engendré par une famille finie d'éléments, si l'idéal est considéré comme un A module) est dit noethérien. La théorie des anneaux noethériens dépasse celle de l'algèbre commutative, contexte des anneaux principaux.

Les bons anneaux d'entiers algébriques, c'est-à-dire ceux qui sont intégralement clôt, disposent de propriétés supplémentaires. Ils vérifient les axiomes caractérisant la structure dite de Dedekind. Ces propriétés permettent d'établir une arithmétique encore analogue à celle des entiers relatifs. Les nombres premiers sont remplacés par les idéaux premiers et tout idéal admet une unique décomposition en idéaux premiers, résultat qui remplace le théorème fondamental de l'arithmétique perdu pour cette configuration.

Notes et références

  1. ↑ Cette définition est par exemple celle utilisé dans le site Idéaux, anneaux, quotients des mathématiques.net
  2. ↑ Cet exemple est développé p 53-55 dans Daniel Perrin, Cours d'algèbre, Éditions de l'École Normale Supérieure de Jeunes Filles, 1981 (ISBN 2-85929-011-7) 
  3. ↑ Cet exemple est tiré de la référence suivante, page 81 : Algèbre commutative par A. Chambert-Loir de l'Université de Rennes I
  4. ↑ Cette définition est par exemple celle du site Dimatu Dictionnaire Mathématiques Universel
  5. ↑ La démonstration est issue de la référence suivante, page 1 et 2 Modules de type fini sur un anneau principal par A. Ducros de l'Université de Rennes I

Liens externes

Références

  • (fr) Nicolas Bourbaki Eléments de mathématique. Algèbre commutative. Chapitre 8 : Dimension. Chapitre 9 : Anneaux locaux noethériens complets Hermann 1983 (ISBN 2225787166)
  • (fr) Daniel Perrin, Géométrie algébrique. Une introduction [détail des éditions]
  • (fr) Jean-Pierre Serre, Cours d'arithmétique [détail des éditions]
Algèbre commutative
Algèbre • Anneau commutatif • Anneau euclidien • Anneau factoriel • Anneau noethérien • Anneau principal • Annulateur • Bimodule • Corps des fractions • Dual d'un module • Facteur direct • Idéal • Longueur d'un module • Module • Module simple • Module fidèle • Module libre • Module monogène • Module quotient • Module semi-simple • Produit tensoriel • Puissance extérieure
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Anneau principal ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Anneau Principal de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Anneau principal — Les anneaux principaux forment un type d anneaux commutatifs important dans la théorie mathématique de la divisibilité. Ce sont des anneaux intègres auxquels on peut étendre deux théorèmes qui, au sens strict, concernent l anneau des entiers… …   Wikipédia en Français

  • Anneau Principal (Jupiter) — L anneau principal est un anneau de la planète Jupiter. Sommaire 1 Caractéristiques 2 Voir aussi 2.1 Liens internes 2.2 Liens externes …   Wikipédia en Français

  • Anneau principal (jupiter) — L anneau principal est un anneau de la planète Jupiter. Sommaire 1 Caractéristiques 2 Voir aussi 2.1 Liens internes 2.2 Liens externes …   Wikipédia en Français

  • Anneau principal (Jupiter) — L anneau principal est un anneau de la planète Jupiter. Sommaire 1 Caractéristiques 2 Voir aussi 2.1 Liens internes 2.2 Liens externes …   Wikipédia en Français

  • Anneau Factoriel — En mathématiques, un anneau factoriel est un cas particulier d anneau commutatif, unitaire et intègre. À l image des nombres entiers, il existe un équivalent du théorème fondamental de l arithmétique pour une telle structure. Tout élément d un… …   Wikipédia en Français

  • Anneau a valuation discrete — Anneau à valuation discrète En mathématiques, un anneau à valuation discrète est un cas particulier d anneau intègre. Il dispose d une structure particulièrement simple puisqu il ne contient qu un unique idéal maximal et qu il est principal. Il… …   Wikipédia en Français

  • Anneau À Valuation Discrète — En mathématiques, un anneau à valuation discrète est un cas particulier d anneau intègre. Il dispose d une structure particulièrement simple puisqu il ne contient qu un unique idéal maximal et qu il est principal. Il est utilisé en théorie… …   Wikipédia en Français

  • Anneau à valuation discrète — En mathématiques, un anneau à valuation discrète est un cas particulier d anneau intègre. Il dispose d une structure particulièrement simple puisqu il ne contient qu un unique idéal maximal et qu il est principal. Il est utilisé en théorie… …   Wikipédia en Français

  • Anneau Euclidien — Euclide (Juste de Gand ,vers 1474) En mathématiques et plus précisément en algèbre, dans le cadre de la théorie des anneaux, un anneau euclidien est un type particulier d anneau commutatif unitaire intègre. Un anneau est dit euclidien s il est… …   Wikipédia en Français

  • Anneau Noethérien — Emmy Noether formalise les propriétés d une famille particulière d anneaux maintenant appelé anneau noethérien. En mathématique, un anneau noethérien est un cas particulier d anneau, c est à dire d un ensemble munis d une addition et d une… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”