Théorie des représentations

L'idée générale de la théorie des représentations est d'essayer d'étudier un groupe G en le faisant agir sur un espace vectoriel V de manière linéaire : on essaie ainsi de voir G comme un groupe de matrices (d'où le terme représentation). On peut ainsi, à partir des propriétés relativement bien connues du groupe des automorphismes de V, arriver à déduire quelques propriétés de G.

Sommaire 1 Quelques définitions 1.1 Définition la plus élémentaire 1.1.1 Cas général 1.1.2 Cas des groupes topologiques : représentation continue 1.2 Définition plus savante 1.2.1 K-algèbre d'un groupe 1.2.2 Lien avec les représentations 1.3 Morphismes 2 Irréductibilité 2.1 Définitions 2.2 Théorème de Maschke 3 Quelques exemples 4 Références 5 Liens

Quelques définitions

Définition la plus élémentaire

Cas général

Soit G un groupe, K un corps et V un espace vectoriel sur K. On appelle représentation de G un morphisme de groupe de G dans GL(V), autrement dit, une application 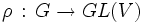telle que ρ(g₁)ρ(g₂) = ρ(g₁g₂), c'est-à-dire que l'application préserve la loi du groupe.

Pour écrire l'action d'un élément g du groupe sur un élément v de l'espace vectoriel à travers la représentation ρ, on notera parfois ρ(g)(v), ρ(g).v ou même g.v s'il n'y a aucune ambiguïté. On note parfois une représentation (V,ρ). On dit parfois également (et abusivement) que V est une représentation de G.

On dit que la représentation est fidèle si le morphisme ρ est injectif. Si par ailleurs V est de dimension finie (cas le plus fréquent), cette représentation permet alors de voir G comme un groupe de matrices. La dimension de V est alors appelée degré de la représentation. Si V est de dimension infinie, alors les ρ(g) sont des opérateurs linéaires.

Cas des groupes topologiques : représentation continue

Si G est un groupe topologique et V a une topologie, la représentation ρ est une représentation continue si l'application Φ de 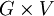dans V définie par 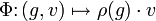est continue. En particulier (et c'est très utile dans le cas des groupes compacts), pour tout 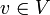l'application 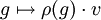est continue.

Définition plus savante

K-algèbre d'un groupe

Notons K[G] le K-espace vectoriel engendré par les éléments de G (c’est-à-dire l'ensemble des combinaisons linéaires formelles finies à coefficients dans K des éléments de G). Un élément générique de K[G] s'écrit

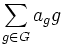
où les a_g sont des éléments de K tous nuls sauf un nombre fini d'entre eux (la somme est donc finie) et où les lettres g sont à considérer comme des symboles formels.

On peut donner à K[G] une structure d'anneau (et donc de K-algèbre) en le munissant de la loi de multiplication (naturelle) suivante :

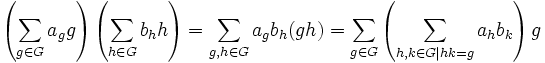
où toutes les sommes sont en fait finies.

K[G] s'appelle la K-algèbre du groupe G.

Lien avec les représentations

On peut alors étendre, et ce de façon unique, la représentation ρ à un morphisme de K-algèbres de K[G] vers End(V), en posant 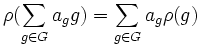. Ceci fait de V un K[G]-module. On dit également que V est un G-module.

Réciproquement, la donnée d'un K[G]-module V fournit une représentation de G.

Morphismes

Un morphisme entre deux représentations (V,ρ) et (W,σ) est simplement une application K-linéaire de V dans W telle que pour tout g appartenant à G on ait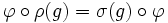

On dit alors aussi que 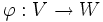est un morphisme G-équivariant.

Deux représentations sont dites semblables, ou isomorphes lorsqu'il existe un isomorphisme G-équivariant entre les espaces correspondants. Il est alors possible de les identifier.

Irréductibilité

Définitions

On dit qu'un module V est simple s'il ne contient pas d'autre sous-module que {0} et V.

Si (V,ρ) est une représentation, on dit que cette représentation est irréductible si V est simple en tant que K[G]-module. Formulé autrement, ceci signifie que V n'admet pas de sous-espace vectoriel propre qui soit stable sous l'action de G. En termes matriciels, cela signifie qu'on ne peut pas trouver de base dans laquelle la représentation de G soit donnée par des matrices ayant toutes la même structure triangulaire supérieure par blocs (avec au moins 2 blocs).

Une représentation est complètement réductible si V est somme directe de sous-espaces stables (par G) irréductibles. En termes de K[G], cela signifie que V peut-être décomposé en somme directe de K[G]-modules simples (on dit alors aussi que V est semi-simple). En termes matriciels, cela signifie qu'on peut trouver une base dans laquelle la représentation de G soit faite par des matrices diagonales par blocs, où chacun des blocs est une représentation irréductible.

Le fait de considérer des modules simples permet de beaucoup simplifier certains raisonnements : par exemple, un morphisme entre deux représentations irréductible est soit nul, soit inversible...

On peut souvent ramener l'étude des représentations de G à l'étude de ses représentations irréductibles : si V n'est pas irréductible, on peut toujours considérer un sous-espace vectoriel de V qui soit stable par G. Si jamais V est de dimension finie, on pourra ainsi finir par trouver un sous-module simple.

Théorème de Maschke

Si G est fini et si la caractéristique de K est nulle ou ne divise pas card(G), alors tout K[G]-module est semi-simple (ou de façon équivalente toute représentation de G dans K est complètement réductible).

En fait, plus généralement, on peut énoncer un théorème similaire pour les groupes compacts (un groupe fini est toujours compact) et les représentations de groupes topologiques.

Quelques exemples

• Commençons par l'exemple le plus trivial : si G est un sous-groupe de GL_n(K), G agit naturellement sur Kⁿ. La représentation associée est appelée représentation standard.

• G agit sur lui-même par multiplication à gauche ; ceci définit une représentation sur K[G]. La représentation associée est appelée représentation régulière. Si G est un groupe fini, toute représentation irréductible est une sous-représentation de la représentation régulière.

Références

• Jean-Pierre Serre, Représentations linéaires des groupes finis [détail des éditions]

Liens

• Représentations d'un groupe fini
• Représentations du groupe symétrique d'indice trois
• Représentations du groupe symétrique d'indice quatre

Algèbre linéaire générale
Vecteur • Scalaire • Combinaison linéaire • Espace vectoriel • Matrice
Famille de vecteurs	Colinéarité • Indépendance linéaire • Famille libre • Rang • Famille génératrice • Base • Théorème de la base incomplète
Sous-espace	Somme d'ensembles • Somme directe • Sous-espace supplémentaire • Dimension d'un espace vectoriel • Codimension • Droite • Plan • Hyperplan
Morphisme et notions relatives	Application linéaire • Noyau • Conoyau • Lemme des noyaux • Pseudo-inverse • Théorème de factorisation • Théorème du rang • Équation linéaire • Système d'équations linéaires • Élimination de Gauss-Jordan • Forme linéaire • Espace dual • Orthogonalité • Base duale • Endomorphisme linéaire • Valeur propre, vecteur propre et espace propre • Spectre • Projecteur • Symétrie • Matrice diagonalisable • Endomorphisme nilpotent
En dimension finie	Trace • Déterminant • Polynôme caractéristique • Polynôme d'endomorphisme • Théorème de Cayley-Hamilton • Polynôme minimal d'un endomorphisme • Invariants de similitude • Réduction d'endomorphisme • Réduction de Jordan • Décomposition de Dunford
Enrichissements de structure	Norme • Produit scalaire • Forme quadratique • Espace vectoriel topologique • Orientation • Algèbre sur un corps • Algèbre de Lie • Complexe différentiel
Développements	Théorie des matrices • Représentation de groupe • Analyse fonctionnelle • Algèbre multilinéaire • Module sur un anneau

• Portail des mathématiques