Module Simple
- Module Simple
-
Module simple
Un module M sur un anneau A est dit simple ou irréductible si et seulement si M n'est pas le module nul et il n'existe pas de sous-modules de M en dehors de {0} et M.
Exemples
- Un espace vectoriel de dimension 1 est un module simple.
- Étant donné un anneau A et I un idéal à gauche non nul de A, I est un A-module simple si et seulement si I est un idéal minimal à gauche.
Propriétés
- Les modules simples sont les modules de longueur 1.
- Un module simple est indécomposable, c'est-à-dire qu'il n'est pas isomorphe à une somme directe de deux modules non nuls. En revanche, la réciproque est fausse.
- Les modules simples sont monogènes, c'est-à-dire engendré par un élément. En effet si x est un élément non nul d'un A-module simple M, alors
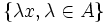 est un sous-module non nul de M, donc c'est M. La réciproque est encore fausse, par exemple le
est un sous-module non nul de M, donc c'est M. La réciproque est encore fausse, par exemple le 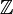 -module
-module 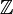 est monogène (engendré par 1) et pourtant
est monogène (engendré par 1) et pourtant 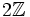 est un sous-module non trivial de
est un sous-module non trivial de 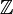 .
.
- Contrairement à ce qui se passe pour des espaces vectoriels, la proposition "tout module non nul possède un sous-module simple" est fausse. En effet
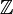 n'est pas simple (point précédent) et tous ses sous-modules sont isomorphes à
n'est pas simple (point précédent) et tous ses sous-modules sont isomorphes à 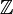 , donc non simples.
, donc non simples.
- Si f est une application A-linéaire entre deux A-modules M et N et si M est simple, alors f est soit nulle, soit injective. En effet, le noyau de f est un sous-module de M, donc {0} ou M.
- Si f est une application A-linéaire entre deux A-modules M et N et si N est simple, alors f est soit surjective, soit nulle. En effet, l'image de f est un sous module de N, donc {0} ou N.
- Les deux résultats précédents impliquent que l'anneau des endomorphismes d'un A-module simple M est un corps. La réciproque de ce résultat est fausse : le
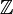 -module
-module  n'est pas simple, et pourtant tout endomorphisme non nul du groupe abélien
n'est pas simple, et pourtant tout endomorphisme non nul du groupe abélien  est inversible.
est inversible.
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégorie : Algèbre générale
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Module Simple de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Module simple — Un module M sur un anneau A est dit simple ou irréductible si M n est pas le module nul et il n existe pas de sous modules de M en dehors de {0} et M. Sommaire 1 Exemples 2 Structure des modules simples 3 Propriétés … Wikipédia en Français
Module Semi-Simple — Camille Jordan, auteur du théorème clé de la théorie En mathématiques et plus particulièrement en algèbre, un A module où A désigne un anneau est qualifié de semi simple ou de complètement réductible si et seulement s il est somme directe de… … Wikipédia en Français
Module Sur Un Anneau — Un module sur un anneau unitaire est une structure algébrique qui généralise celle d espace vectoriel et celle d idéal d un anneau. Dans un espace vectoriel l ensemble des scalaires forme un corps tandis que dans un module, ceux ci sont de… … Wikipédia en Français
Module Fidèle — Un module M sur un anneau A e est dit fidèle si son annulateur est réduit à {0}, en d autres termes, si l action de chaque est non triviale ( pour un certain ). Autrement dit, un module est fidèle si la représentation associée est injective. À… … Wikipédia en Français
Module Libre — En mathématiques, en algèbre, un module libre est un module qui possède une base. Étant donné un anneau A, l exemple le plus immédiat de A module libre est An. Soit M un R module, l ensemble E = {e1, e2, ... en} est une base libre pour M si … Wikipédia en Français
Module fidele — Module fidèle Un module M sur un anneau A e est dit fidèle si son annulateur est réduit à {0}, en d autres termes, si l action de chaque est non triviale ( pour un certain ). Autrement dit, un module est fidèle si la représentation associée est… … Wikipédia en Français
Module Monogène — Un module monogène est un module qui peut être engendré par un seul élément, par exemple est engendré par 1. Algèbre commutative Algèbre • Anneau commutatif • Anneau euclidien • Anneau factoriel • Anneau noethérien • Anneau principal • Annulateur … Wikipédia en Français
Module monogene — Module monogène Un module monogène est un module qui peut être engendré par un seul élément, par exemple est engendré par 1. Algèbre commutative Algèbre • Anneau commutatif • Anneau euclidien • Anneau factoriel • Anneau noethérien • Anneau… … Wikipédia en Français
Module semi-simple — Camille Jordan, auteur du théorème clé de la théorie En mathématiques et plus précisément en algèbre non commutative, un module sur un anneau est dit semi simple ou complètement réductible s il est somme directe de sous modules simples ou, ce qui … Wikipédia en Français
Module sur un anneau — En mathématiques, au sein des structures algébriques, « un module est à un anneau ce qu un espace vectoriel est à un corps »[1] : pour un espace vectoriel, l ensemble des scalaires forme un corps tandis que pour un module, cet… … Wikipédia en Français
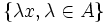 est un sous-module non nul de M, donc c'est M. La réciproque est encore fausse, par exemple le
est un sous-module non nul de M, donc c'est M. La réciproque est encore fausse, par exemple le 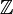 -module
-module 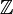 est monogène (engendré par 1) et pourtant
est monogène (engendré par 1) et pourtant 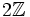 est un sous-module non trivial de
est un sous-module non trivial de 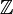 .
.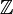 n'est pas simple (point précédent) et tous ses sous-modules sont isomorphes à
n'est pas simple (point précédent) et tous ses sous-modules sont isomorphes à 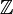 , donc non simples.
, donc non simples.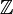 -module
-module  n'est pas simple, et pourtant tout endomorphisme non nul du groupe abélien
n'est pas simple, et pourtant tout endomorphisme non nul du groupe abélien  est inversible.
est inversible.