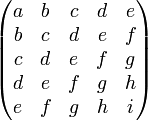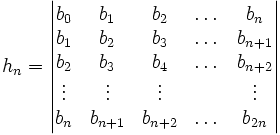Matrice de hankel

Matrice de Hankel

En algèbre linéaire une matrice de Hankel, du nom du mathématicien Hermann Hankel, est une matrice carrée dont les valeurs sont constantes le long des diagonales ascendantes, c'est-à-dire dont les indices vérifient la relation $a i, j = a i - 1, j + 1$

Par exemple une matrice de Hankel de taille 5 s'écrit sous la forme

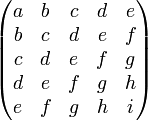
$\begin{pmatrix} a & b & c & d & e \\ b & c & d & e & f \\ c & d & e & f & g \\ d & e & f & g & h \\ e & f & g & h & i \end{pmatrix}$

Cette matrice a une certaine parenté avec les matrices de Toeplitz (ces dernières sont des matrices de Hankel renversées).

Sur un espace de Hilbert muni d'une base hilbertienne, on peut définir plus généralement un opérateur de Hankel. Ce dernier admet pour représentation une matrice de Hankel infinie, c'est-à-dire que le coefficient $a i, j = (e i | a (e j))$ , dépend seulement de $i + j$ .

Déterminant et transformation de Hankel

À toute suite $(b n)$ on peut associer la suite des déterminants $h n$ des matrices de Hankel successives^[1]

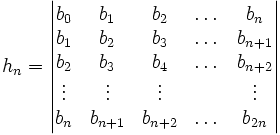
$h_n = \begin{vmatrix} b_0 &b_1&b_2&\dots&b_{n}\\ b_1 &b_2&b_3&\dots&b_{n+1}\\ b_2 &b_3&b_4&\dots&b_{n+2}\\ \vdots&\vdots&\vdots&&\vdots\\ b_{n} &b_{n+1}&b_{n+2}&\dots&b_{2n}\\ \end{vmatrix}$

une suite est nulle si et seulement si sa transformée de Hankel est nulle

une suite vérifie une relation de récurrence linéaire à coefficients constants si et seulement si la transformée de Hankel est nulle à partir d'un certain rang.

Voir aussi

Articles en rapport avec les matrices
Par forme	carrée • triangulaire • diagonale • tridiagonale • élémentaire • échelonnée • creuse • aléatoire • circulante • de Hankel • de Toeplitz • de Vandermonde
Transformée	transposée • adjointe • inverse • Comatrice
En relation	équivalente • semblable • congruente
Par propriété	inversible • diagonalisable • trigonalisable • symétrique • antisymétrique • hermitienne • normale • orthogonale • unitaire • symplectique • de Hadamard • définie positive • à diagonale dominante • nilpotente
Par famille	identité • de De Casteljau • de Cartan • de Hilbert • de Mueller • de Pauli • de Dirac
Particulière	CKM
Associée	de permutation • de passage • compagnon • de Sylvester • d'adjacence • laplacienne • hessienne • jacobienne • génératrice • de contrôle • de corrélation • de Gram • de variance-covariance • d'inertie • de Jones • des gains • stochastique
Résultats	décompositions : LU • QR • polaire • valeurs singulières Trigonalisation • Réduction de Jordan • facteurs invariants
Voir aussi	Théorie des matrices • Algèbre linéaire

Notes et références

↑ (en) John W. Layman, The Hankel Transform and some of its properties, Journal of Integer Sequences, vol 4 (2001)

Portail des mathématiques

Ce document provient de « Matrice de Hankel ».

Catégories : Matrice remarquable | Déterminant

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Matrice de hankel de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Matrice De Hankel — En algèbre linéaire une matrice de Hankel, du nom du mathématicien Hermann Hankel, est une matrice carrée dont les valeurs sont constantes le long des diagonales ascendantes, c est à dire dont les indices vérifient la relation ai,j = ai − 1,j + 1 … Wikipédia en Français
Matrice de Hankel — En algèbre linéaire une matrice de Hankel, du nom du mathématicien Hermann Hankel, est une matrice carrée dont les valeurs sont constantes le long des diagonales ascendantes, c est à dire dont les indices vérifient la relation ai,j = ai − 1,j + 1 … Wikipédia en Français
Matrice de Toeplitz — En algèbre linéaire, une matrice de Toeplitz (d après Otto Toeplitz) ou matrice à diagonales constantes est une matrice dont les coefficients sur une diagonale descendant de gauche à droite sont les mêmes. Par exemple, la matrice suivante est une … Wikipédia en Français
Matrice (algèbre) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice (mathematiques) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice carrée — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice Diagonalisable — En algèbre linéaire, une matrice carrée M d ordre n ( ) à coefficients dans un corps commutatif K, est dite diagonalisable si elle est semblable à une matrice diagonale, c est à dire s il existe une matrice inversible P et une matrice diagonale D … Wikipédia en Français
Matrice Définie Positive — En algèbre linéaire, la notion de matrice définie positive est analogue à celle de nombre réel strictement positif. On introduit tout d abord les notations suivantes ; si a est une matrice à éléments réels ou complexes : aT désigne la… … Wikipédia en Français
Matrice Inversible — En mathématiques et plus particulièrement en algèbre linéaire, une matrice carrée A d ordre n est dite inversible ou régulière ou encore non singulière, s il existe une matrice B d ordre n telle que AB = BA = In, ( AB = In suffit d aprés le… … Wikipédia en Français
Matrice definie positive — Matrice définie positive En algèbre linéaire, la notion de matrice définie positive est analogue à celle de nombre réel strictement positif. On introduit tout d abord les notations suivantes ; si a est une matrice à éléments réels ou… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Matrice de hankel