Anneau De Dedekind

Anneau De Dedekind

Anneau de Dedekind

Richard Dedekind définit et établit les bases de la théorie des anneaux portant maintenant son nom.

En mathématiques, un anneau de Dedekind est un anneau disposant de propriétés particulières. Sa formalisation initiale a pour objectif la description d'un ensemble d'entiers algébriques, ce concept est aussi utilisé en géométrie algébrique.

Un anneau de Dedekind doit son origine à la théorie algébrique des nombres. Pour résoudre des équations comme celle du dernier théorème de Fermat, l'anneau des entiers relatifs s'avère mal commode. Il est parfois plus simple de considérer d'autres anneaux, comme celui des entiers de Gauss, d'Eisenstein ou de Dirichlet. Le théorème des deux carrés de Fermat ou encore l'équation de Pell-Fermat illustre l'utilité d'une telle structure. Leurs études se fondent sur le cas particulier des entiers quadratiques, plus simple que le cas général.

Cette formulation est l'œuvre[1] de Richard Dedekind et date de la fin du XIXe siècle.

Sommaire

Définitions

Trois définitions sont nécessaires pour aborder celle de l'article. Soit K un corps commutatif et A un anneau unitaire inclus dans K.

  • Un élément k de K est dit entier algébrique sur A si et seulement si son polynôme minimal existe et est à coefficients dans A.
  • L'ensemble des entiers algébriques sur A de K forme un anneau appelé fermeture intégrale de A dans K[2].

L'ensemble est non vide car il contient A, le fait qu'il forme un anneau est une conséquence des propriétés du polynôme minimal.

Soit maintenant A un anneau unitaire intègre. Il se prolonge en un corps des fractions K. La méthode est l'analogue de celle permettant de construire l'ensemble des nombres rationnels à partir des entiers relatifs.

  • L'anneau A est dit intégralement clos si et seulement s'il est égal à la fermeture intégrale de son corps des fractions[3].

Un anneau de Dedekind est un anneau vérifiant quatre familles de propriétés :

  • Un anneau est dit de Dedekind si et seulement si :
  1. Il est commutatif unitaire intègre.
  2. Il est noethérien.
  3. Il est intégralement clos.
  4. Tout idéal premier non nul de l'anneau est maximal[4].

Remarque : Un anneau commutatif unitaire intègre est dit noethérien si et seulement si toute suite croissante d'idéaux est stationnaire, c'est-à-dire constante à partir d'un certain rang.

Histoire

Premiers essais

Leonhard Euler utilise pour la première fois un anneau d'entiers algébriques.

L'histoire initiale de l'étude des anneaux de Dedekind se confond avec celles des entiers algébriques. En 1753, Leonhard Euler (1707 - 1783) écrit à Goldbach qu'il a trouvé une preuve du dernier théorème de Fermat pour n égal à trois. Elle se fonde[5] sur l'utilisation de l'anneau des nombres de la forme a + b.i√3 où a et b sont des entiers relatifs et i l'unité imaginaire. La preuve s'avère fausse car, contrairement à ce qu'imagine le mathématicien, un tel anneau n'est pas factoriel c'est à dire qu'il n'existe pas une unique décomposition en facteurs premiers, un contre exemple est donné par les deux décompositions suivantes :

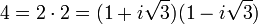
4 = 2\cdot2 = (1 + i\sqrt 3)(1- i\sqrt 3)\;

Si l'application est encore approximative, l'utilisation d'ensemble de nombres de cette nature s'avère fructueuse. Carl Friedrich Gauss (1777 1855) étudie[6] les nombres de la forme a + i.b permettant, par exemple de fournir des preuves élégantes du théorème des deux carrés de Fermat, ils sont maintenant dénommés entiers de Gauss. Ferdinand Eisenstein (1823 1852) analyse l'anneau des entiers portant son nom et qui offre une démonstration rigoureuse du grand théorème de Fermat pour n égal à trois analogue à celle d'Euler.

Groupe des unités

Dirichlet établit le théorème clé associé aux unités d'un anneau d'entiers.

La résolution générale du dernier théorème de Fermat amène l'étude d'autres anneaux d'entiers. Johann Peter Gustav Lejeune Dirichlet (1805 - 1859) comprend que, pour les valeurs supérieures de n, une première obstruction rend la démonstration plus technique. Il utilise l'anneau maintenant appelé des entiers de Dirichlet formé des nombres de la forme a + b.1/2 (1 + √5). L'obstruction réside dans le fait que, si l'anneau est bien euclidien, l'ensemble des éléments inversibles encore appelé groupe des unités devient infini. Pour ces éléments, aucun outil classique de la théorie des anneaux, comme la décomposition en facteurs premiers n'est possible. Il parvient néanmoins à trouver une preuve[7] complétée quelques mois plus tard par Adrien-Marie Legendre (1752 - 1833).

Cette analyse du groupe des unités dans le cas d'entiers quadratiques revient à l'étude de la structure des solutions de l'équation de Pell-Fermat. Une élucidation générale de la structure du groupe des unités d'une fermeture intégrale est finalement donnée par Dirichlet[8] et porte maintenant le nom de théorème des unités de Dirichlet.

La compréhension de la structure du groupe des unités ne permet néanmoins pas de venir à bout du dernier théorème de Fermat. Gabriel Lamé (1795 - 1870) prouve bien, quatorze ans après Dirichlet, l'absence de solution pour n égal à sept à l'aide d'un anneau entiers quadratique comportant un groupe des unités infini[9]. Cependant la preuve est complexe et non généralisable.

Deuxième obstruction

Ernst Kummer comprend comment contourner la deuxième obstruction.

Lamé croit trouver une solution générale[10] en utilisant l'anneau des entiers d'un corps cyclotomique. Un corps cyclotomique d'indice n est le plus petit corps contenant les racines nième de l'unité du corps des complexes. L'anneau des entiers est celui des nombres du corps racine d'un polynôme unitaire à coefficients entiers relatifs. Son erreur consiste à supposer, en terme moderne que l'anneau est factoriel, c'est-à-dire que le théorème fondamental de l'arithmétique s'applique sur une structure de cette nature.

Cette propriété, que l'on sait être fausse dans le cas général pour les anneaux d'entiers quadratiques n'est pas non plus vérifiée pour les entiers cyclotomiques. En 1844, soit trois ans plus tôt, Ernst Kummer (1810 - 1893) avait établi cette absence de propriété dans le cas général en exhibant un contre exemple, les entiers du corps cyclotomiques des racines 23ièmes de l'unité[11].

L'absence de factorialité de ce type d'anneau est, à la suite de Kummer considéré comme la deuxième obstruction pour les anneaux de cette nature[12]. Une manière d'interpréter cette difficulté consiste à considérer qu'il manque des nombres pour assurer l'unicité de la décomposition en facteurs premiers. Kummer définit des nombres idéaux palliant les manques et permettant d'exprimer une nouvelle forme de théorème fondamental de l'arithmétique. Elle lui permet de démontrer[13] le dernier théorème de Fermat pour toute valeur de n jusqu'à 100, à l'exception des nombres premiers réguliers, c'est-à-dire 37, 59 et 67.

Formalisme de Dedekind

A l'instar de Leopold Kronecker (1823 - 1891) l'objectif de Dedekind est de généraliser les résultats de Kummer à tout fermeture intégrale d'un corps de nombre et non pas seulement aux corps cyclotomiques. Leurs philosophies sont néanmoins opposées, l'objectif de Dedekind est en rupture avec la tradition calculatoire de Gauss et Kummer. Il cherche à démontrer les propriétés de ces anneaux à l'aide de leurs caractéristiques fondamentales et non pas le fruit de calculs complexes[14].

A cette occasion, il formalise la notion d'idéal[15] et d'idéal principal. La multiplication des idéaux principaux correspond à celles de leurs générateurs et se généralise à tous les idéaux. L'objectif est alors de montrer que tout idéal se décompose de manière unique en un produit d'idéaux premiers. Les nombres idéaux de Kummer deviennent les idéaux premiers non principaux. Un outil essentiel est l'idéal fractionnaire qu'il formalise[16] en 1876. Elle confère à l'ensemble des idéaux une structure de groupe abélien dont un sous-groupe est composé des idéaux fractionnaires principaux et permet d'exprimer le théorème fondamental sur la structure des idéaux premiers non principaux : Le groupe quotient des idéaux fractionnaires par les idéaux fractionnaires principaux est fini dans le cas d'une fermeture intégrale d'un corps de nombres algébriques. Ce groupe quotient est appelé groupe des classes d'idéaux. Il démontre[1] ce résultat dans toute sa généralité à la fin du siècle[17].

XXe siècle

A la différence des anneaux principaux, les cas d'anneaux de Dedekind sont finalement fréquents. De plus, ils ne se limitent pas aux fermetures intégrales d'extension de corps. Un vaste sujet utilise largement cette structure : la géométrie algébrique. Les entiers relatifs sont remplacés par un anneau de polynômes sur un corps fini et le corps de nombre par un corps de fonctions. Un tel anneau vérifie encore les axiomes de Dedekind.

De nouveaux outils comme la valuation sont développés et les anneaux à valuations discrètes permettent d'étudier de nouvelles structures comme les nombres p-adiques.

Exemples

Entier algébrique

Le premier exemple est donné par l'ensemble des entiers algébriques d'une extension finie du corps des rationnels. Une première famille d'anneau de cette nature est celle des entiers quadratiques correspondant aux entiers d'une extension quadratique. Deux cas particuliers simples sont les entiers de Gauss et ceux d'Eisenstein. Ces deux anneaux sont euclidiens et le groupe des unités est fini, et même cyclique. Les entiers de Dirichlet mettent en évidence une obstruction, le groupe des unités est infini. Les anneaux d'entiers quadratiques permettent d'analyser les deux obstructions et d'en comprendre leur nature à l'aide d'une étude plus simple que celle du cas général.

Un exemple très étudié est celui de la fermeture intégrale d'une extension cyclotomique, c'est-à-dire d'une extension contenant toutes les racines d'un polynôme cyclotomique. La théorie de Galois est particulièrement riche pour les corps de cette nature. Les extensions sont non seulement galoisiennes, mais aussi abéliennes.

Dans le cas général, soit K une extension finie de Q et n la dimension de K sur Q, qui ici désigne l'ensemble des rationnels :

  • La fermeture intégrale OK de K est un anneau de Dedekind.

La démonstration proposée ici utilise les outils de la théorie de Galois ainsi que la forme trace et le polynôme minimal.

Démonstration
  • L'anneau OK est commutatif unitaire intègre :

OK est non vide car il contient Z, l'ensemble des entiers relatifs. Si a et b sont deux éléments de OK, alors a.b et a - b sont aussi des éléments de OK. Cette propriété est démontrée dans un cadre général dans l'article Polynôme minimal d'un nombre algébrique. Comme OK contient Z, il contient un et l'anneau est unitaire. L'anneau est formé des éléments d'un sous ensemble d'un corps commutatif, il est donc commutatif et intègre.

Une démonstration dans un cadre plus générale est proposée dans l'article associée.

  • Le quotient de OK par un idéal P est de cardinal fini :

Remarquons dans un premier temps que tout idéal P de OK est un Z module de dimension n. L'article Groupe abélien de type fini montre que P est un Z module de type fini et comme OK est libre il est aussi libre. Soit p un élément de P. L'application de OK dans P, qui à x associe p.x est un morphisme injectif de OK dans P et l'idéal P contient une famille libre de cardinal n. Comme il est inclus dans un Z module de dimension n, il est de dimension n.

Le quotient de OK par P est un groupe de type fini et ne contenant que des éléments de torsions. En effet, soit h un élément de OK, il est combinaison linéaire d'une base de P en tant qu'élément de l'espace vectoriel K. Quitte à multiplier la combinaison linéaire par le produit des dénominateurs des coefficients non nuls de la combinaison linéaire, on obtient une combinaison linéaire à coefficients dans Z d'un multiple de h exprimé dans la base de P, ce qui montre qu'un multiple de h est élément de P. Cette propriété exprime exactement le fait que l'image de h dans le groupe quotient est un élément de torsion. Un groupe abélien de type fini ne contenant que des éléments de torsion est un groupe fini, ce qui termine la démonstration de cette propriété.

  • Tout idéal premier P de OK est maximal :

Le quotient de OK par P est un anneau intègre si P est premier. Tout anneau intègre fini est un corps, ce qui montre que P est maximal.

  • L'anneau OK est intégralement clos :

Montrons que le corps des fractions de OK est égal à K. Son corps des fractions est inclus dans K car K est un corps. Réciproquement, montrons que tout élément de K s'écrit comme une fraction d'un élément de OK divisé par un élément non nul de Z. Soit k un élément de K, la preuve du fait que OK est noethérien montre l'existence d'un élément non nul an tel que ank est un élément h de OK. On en déduit que k est égal à h/an et est donc bien égal à un élément de OK divisé par un élément non nul de Z.

Soit h un entier algébrique du corps des fractions de OK. Le sous-anneau engendré par h et par les coefficients du polynôme minimal est un Z module de type fini d'après l'article Polynôme minimal d'un nombre algébrique. Il existe ainsi une sous-algèbre sur Z contenant h est de dimension finie, ce qui implique que h est entier dans K et donc élément de OK.

 

Géométrie algébrique

Si les extensions finies des nombres rationnels contiennent des fermetures intégrales jouissant des propriétés d'un anneau de Dedekind, il en est de même pour les extensions finis de F(X). Ici F désigne un corps fini et F(X) le corps des fractions rationnelles. Cet ensemble est le corps des fractions des polynômes formels à coefficients dans F.

Une extension finie de F(X) est appelé un corps de fonctions. Il est possible d'y étudier les fermetures intégrales. Si les analogies sont nombreuses, l'arithmétique sur un corps de fonctions est souvent plus facile que sur un corps de nombres[18]. Plusieurs raisons sont à l'origine de la simplification. Les valeurs absolues sur les corps de fonctions sont toutes ultramétrique, en revanche il en existe une archimédienne sur les nombres rationnels. Les corps de fonctions disposent d'un outil bien utile, la dérivation, qui n'existe pas pour les corps de nombres. Enfin, il est possible de considérer le produit tensoriel \scriptstyle {F[X]\otimes F[X]}, qui n'a pas d'équivalent intéressant sur les corps de nombres.

Propriétés

Idéal fractionnaire

Article détaillé : Idéal fractionnaire.

Une propriété essentielle d'un anneau de Dedekind réside dans le fait que tout idéal non nul se décompose de manière unique en un produit d'idéaux premiers. Ce résultat remplace le théorème fondamental de l'arithmétique dans le cas d'un anneau factoriel. Pour établir ces propriétés, il est utile de munir l'ensemble des idéaux d'une multiplication. Le produit de deux idéaux I1 et I2 est le plus petit idéal contenant tous les produits a.b si a (resp. b) est élément de I1 (resp. I2). Le produit est associatif, il admet un élément neutre l'anneau tout entier et est associatif. Il est alors commode d'enrichir l'ensemble de tous les inverses, la structure devenant alors un groupe abélien.

Les propriétés des idéaux et idéaux fractionnaires caractérisent un anneau de Dedekind. Plus précisément, on dispose des propriétés suivantes :

  • Soit A un anneau commutatif unitaire intègre, noethérien et K son corps des fractions, les propriétés suivantes sont équivalentes :
  1. L'anneau A est de Dedekind.
  2. Tout idéal premier non nul de A est inversible.
  3. Tout idéal premier non nul est maximal et pour tout idéal maximal M le A/M espace vectoriel M/M2 est de dimension un.
  • Soit A un anneau commutatif unitaire, les propriétés suivantes sont équivalentes :
--L'anneau A est de Dedekind.
--Tous les idéaux non nuls de A sont inversibles (cette hypothèse implique en particulier que l'anneau A est intègre et noethérien).
--Tout idéal premier non nul de A est inversible (inutile de supposer l'anneau intègre et noethérien, car de manière générale dans les anneaux commutatifs unitaires, tout idéal non inversible est inclus dans un idéal premier non inversible).

Le groupe des classes d'idéaux est le quotient du groupe des idéaux fractionnaires non nuls par le sous-groupe des idéaux fractionnaires principaux. Sa structure renferme d'importantes propriétés de l'anneau de Dedekind. Dans le cas d'une fermeture intégrale d'un corps de nombres de dimension finie sur Q, le groupe des classes est d'ordre fini.

Démonstration
  • (1) implique (2) :

La démonstration est donnée dans l'article détaillé.

  • (2) implique (1) :

Montrons dans un premier temps que A est intégralement clos. Soit h un entier algébrique non nul sur A de K. Dire que h est un entier algébrique revient à dire que :

(1)\quad \exists (a_i)_{i \in [0,n-1]} \in \mathbb A^n \quad h^n + a_{n-1}h^{n-1} + \cdots + a_0 = 0

Montrer que h est élément de A est équivalent à dire que h.A est un idéal non fractionnaire. L'article détaillé montre que cette proposition revient à dire que, si P est un idéal premier, vP(h) l'exposant de P dans la décomposition en idéaux premiers de h.A est positif. Supposons qu'il existe un idéal premier M tel que vM(h) soit strictement négatif alors :

\forall i \in [0, n-1],\quad v_{\mathfrak M}(h^n)= nv_{\mathfrak M}(h)< v_{\mathfrak M}(h^{n-i})\le v_{\mathfrak M}(a_{n-i} h^{n-i})

L'exposant de M de l'idéal fractionnaire engendré par une somme d'éléments de K est supérieur ou égal au minimum des exposants de l'idéal engendré par chaque éléments, on en déduit :

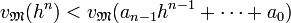
v_{\mathfrak M}(h^n) < v_{\mathfrak M}(a_{n-1}h^{n-1} + \cdots + a_0)

Ce qui contredit l'égalité suivante, conséquence de (1) :

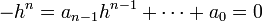
-h^n=a_{n-1}h^{n-1} + \cdots + a_0 = 0\;

On en déduit que pour tout idéal premier P, vP(h) est positif, ce qui montre que h est un élément de A.

Montrons enfin que tout idéal premier non nul P est maximal. Il existe un idéal M maximal le contenant, l'objectif est de montrer que P est égal à M. Comme tout idéal maximal est inversible car premier et que la multiplication des idéaux est commutative et associative :

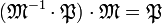
(\mathfrak M^{-1}\cdot \mathfrak P)\cdot \mathfrak M = \mathfrak P

On remarque que M−1.P est inclus dans A car P est inclus dans M, on en déduit que M−1.P est un idéal. Comme P est premier, soit M−1.P est inclus dans P soit M est inclus dans P. Si M est inclus dans P, alors P est égal à M et P est maximal. Il suffit pour conclure de montrer que M−1.P n'est pas inclus dans P. Raisonnons par l'absurde, si M−1.P est inclus dans P alors :

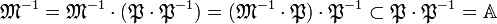
\mathfrak M^{-1} = \mathfrak M^{-1}\cdot(\mathfrak P\cdot\mathfrak P^{-1})= (\mathfrak M^{-1}\cdot\mathfrak P)\cdot\mathfrak P^{-1}\subset \mathfrak P\cdot\mathfrak P^{-1} = \mathbb A

L'idéal fractionnaire M−1 n'est pas inclus dans A car A.M est inclus dans M et ne peut être égal à A, ce qui termine la démonstration.

  • (1) implique (3) :

Remarquons dans un premier temps que M est un idéal maximal, A / M est bien un corps. De plus, l'article détaillé montre que la décomposition d'un idéal en idéaux premiers est unique, en conséquence M et M 2 sont distincts et M / M 2 n'est pas réduit à l'élément neutre. Soit V un sous-espace vectoriel de M / M 2 non réduit à l'élément neutre, son image réciproque par le morphisme canonique de M vers M / M 2 est un idéal N contenant strictement M2 et contenu dans M. Ceci montre que N.M −1 est un idéal contenant strictement M, il n'en existe qu'un l'anneau A car M est maximal. L'égalité N.M −1 = A montre que N est égal à M. Le seul sous-espace vectoriel différent de l'élément neutre de M / M 2 est l'espace lui-même, ce qui montre que l'espace est de dimension un.

  • (3) implique (2) :

Soit M un idéal premier non nul, l'objectif est de montrer qu'il existe un idéal fractionnaire F tel que M.F est égal à A. On définit F par :

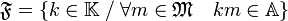
\mathfrak F = \{k \in \mathbb K\; /\; \forall m \in \mathfrak M \quad km \in \mathbb A\}\;

On remarque de F est un sous A module de K et si m est un élément de M, alors m.F est inclus dans A, ce qui montre que F est un idéal fractionnaire.

On remarque de F.M est un idéal contenant M, M est premier, il est donc maximal par hypothèse. Il suffit donc de montrer que F.M contient un élément qui n'est pas dans M pour conclure. Pour cela, un lemme est utile :

  • Soit P1, ..., Pr une famille d'idéaux premiers de A, il existe un morphisme surjectif cannonique φ entre les deux structures suivantes :
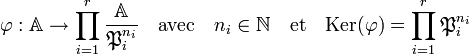
\varphi : \mathbb A \rightarrow \prod_{i=1}^r \frac {\mathbb A}{\mathfrak P_i^{n_i}}\quad \text{avec}\quad n_i \in \mathbb N\quad \text{et}\quad \text{Ker}(\varphi) = \prod_{i=1}^r \mathfrak P_i^{n_i}
Ce résultat est une conséquence du théorème des restes chinois. Il suffit de montrer que Pini + Pjnj est égal à A si i est différent de j.
Montrons ce résultat pas récurrence sur ni + nj. Le résultat est vrai si la somme est égale à deux car tout idéal premier est maximal. Supposons le résultat vrai pour toute somme strictement inférieure à p et montrons qu'elle est vraie pour toute somme égale à p (p est strictement supérieur à deux). Soit deux valeurs ni et nj tel que la somme soit égale à p. L'un des deux termes est supérieur à deux, supposons que ce soit ni. Par hypothèse de récurrence, Pini - 1 + Pjnj contient un. Il existe ainsi α élément de Pini - 1 et β élément de Pjnj tel que α + β = 1. L'élément α est dans Pi il existe donc une famille finie (a k ) d'éléments de Pi et (αk ) d'éléments de Pini - 1 tel que :
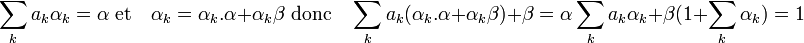
\sum_k a_k\alpha_k = \alpha \;\text{et}\quad \alpha_k = \alpha_k.\alpha + \alpha_k\beta\;\text{donc}\quad \sum_k a_k(\alpha_k.\alpha + \alpha_k\beta) + \beta = \alpha\sum_k a_k\alpha_k + \beta(1 + \sum_k\alpha_k) = 1
On en déduit que 1 est somme d'un élément de Pini et d'un élément de Pjnj. La conclusion du lemme est la conséquence du théorème chinois.

Soit m un élément M qui n'est pas dans M2, il existe au moins un élément de cette nature, sinon le quotient M / M2 ne pourrait être une droite vectoriel. Une propriété des anneaux noethériens (démontrée dans l'article Anneau noethérien) montre l'existence d'une famille d'idéaux premiers (Pi) de A et d'entiers positifs (ni) pour i variant de 1 à r tel que :

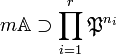
m\mathbb A \supset \prod_{i=1}^r \mathfrak P^{n_i}\;

On choisit de plus P1 égal à M. Soit a un élément de a tel que φ(a) = (1,0, ..., 0), c'est-à-dire que a est élément de Pini si i est strictement supérieur à 1 et a est élément de la classe de 1 dans le quotient de A par M n1.

  • La fraction de K : a / m est dans l'idéal fractionnaire F :
L'objectif est de montrer que si x est élément de M, alors a.x.m-1 est élément de A, ou encore que a.x est dans mA. Comme l'idéal mA contient le produit des idéaux Pini, cette condition est équivalente à φ(a.x) est élément de φ(m.A), c'est à dire que la classe de x est un multiple de la classe m dans le quotient A / M n1. Comme M / M 2 est un espace vectoriel de dimension 1, il existe a1 dans A tel que x = a1.m + x2 avec x2 élément de M 2. De même, mk engendre M k / M k+1, ce qui montre que :
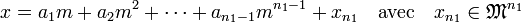
x = a_1m + a_2m^2 + \cdots + a_{n_1-1}m^{n_1-1} + x_{n_1} \quad \text{avec}\quad x_{n_1} \in \mathfrak M^{n_1}
Par passage au quotient dans A / M n1, on obtient :
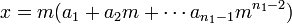
x = m(a_1 + a_2m + \cdots a_{n_1-1}m^{n_1-2})\;
Ce qui montre que la classe de x est bien un multiple de la classe de m et donc que la fraction de K a / m est dans l'idéal fractionnaire F.

L'élément a n'est pas dans M car tout élément de M est nilpotent dans A / M n1. L'élément a est M.F car a = m.a / m, il existe ainsi un élément a de M.F qui n'est pas dans M, M est un idéal maximal et M.F un idéal contenant M et a, il est donc égal à A. Ce qui montre que M est inversible et termine la démonstration.

 

Valuation

Article détaillé : Valuation.

L'unicité de la décomposition d'un idéal en idéaux premiers permet la définition d'une famille de fonctions appelées valuations. La valuation en P, ou P désigne un idéal premier non nul, est une fonction de l'ensemble des idéaux de A dans N l'ensemble des entiers positifs qui à un idéal non nul J associe n, égal au plus petit entier tel que P n contienne J. Cette fonction est souvent notée : vP(J ). Cette fonction se prolonge sur les idéaux fractionnaires de A, elle prend alors ces valeurs dans Z l'ensemble des entiers relatifs. Si π désigne l'ensemble des idéaux premiers et F un idéal fractionnaire :

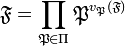
\mathfrak F = \prod_{\mathfrak P \in \Pi} \mathfrak P^{v_{\mathfrak P}(\mathfrak F)}

La fonction qui à P associe vP(F ) est nulle presque partout, c'est-à-dire que le produit précédent ne contient qu'un nombre fini de facteurs différent de l'élément neutre des anneaux, c'est-à-dire A. La décomposition introduit un isomorphisme entre le groupe des idéaux fractionnaires et le groupe libre Z(π) l'ensemble des fonctions de support presque nul (la fonction est nulle sauf peut être sur un ensemble fini de points) à valeurs dans Z.

La fonction valuation se prolonge sur K le corps des fractions de l'anneau de Dedekind A, à un élément k, vP(k) est égal à l'image par vP de l'idéal fractionnaire kA.

La fonctions valuations disposent de nombreuses propriétés cité dans l'article Idéal fractionnaire. On peut citer, par exemple, le fait qu'un élément a de K est entier algébrique si et seulement si toutes ses valuations sont positives.

Localisation

Article détaillé : Anneau à valuation discrète.

Une structure utile pour l'analyse d'un anneau de Dedekind est un anneau de fractions particulier. Si P est un idéal premier non nul, le localisé de A en P désigne l'ensemble des fractions a / b tel que a est élément de A et b un élément de A qui n'est pas dans P. Il est souvent noté A(P), c'est un anneau principal n'ayant qu'un unique idéal premier. Sa structure est celle d'un anneau à valuation discrète. Comme les idéaux fractionnaires, la structure des localisés de A caractérise les anneaux de Dedekind, plus précisément :

  • Soit A un anneau commutatif unitaire intègre noethérien. L'anneau A est de Dedekind si et seulement si pour tout idéal premier non nul P, le localisé de A en P est un anneau à valuation discrète.
Démonstration
  • Si A est de Dedekind, alors le localisé de A en P est un anneau à valuation discrète :

On note A(P) le localisé de A en P.

  • L'anneau A(P) est intégralement clos :
L'objectif est de montrer qu'un élément k du corps des fraction K de A entier sur A(P) est un élément de A(P). Il existe une suite d'éléments (ai) pour i variant de 0 à n - 1 et un élément b de A - P tel que :
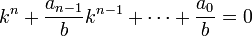
k^n + \frac {a_{n-1}}bk^{n-1} + \cdots + \frac {a_0}b = 0 \;
On en déduit que b.k est entier sur A, c'est donc un élément a de A. En conséquence k est égal à a / b avec a élément de A et b élément de A - P, ce qui montre que k est élément de A(P) et termine la démonstration du lemme.

L'anneau A(P) est intégralement clos et est le localisé d'un anneau noethérien, il est donc noethérien. Une démonstration est proposée dans l'article Anneau noethérien. Le fait que A(P) soit un anneau commutatif, unitaire, intègre, noethérien, avec un unique idéal premier montre qu'il est à valuation discrète. Une démonstration est proposée dans l'article détaillé.

  • Si A(P) est un anneau à valuation discrète pour tout idéal premier non nul, alors A est de Dedekind :

Soit P un idéal premier non nul de A, l'objectif est de montrer qu'il est inversible, dans ce cas, les résultats du paragraphe précédent montrent que l'anneau A est de Dedekind. Soit F l'idéal fractionnaire défini par :

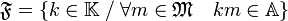
\mathfrak F = \{k \in \mathbb K\; /\; \forall m \in \mathfrak M \quad km \in \mathbb A\}\;

Supposons que P.F soit différent de A, Il existe alors un idéal M contenant le produit strictement P.F. Soit (pi) pour i variant de 1 à n une famille génératrice de P comme A module. PA(M) est un idéal de A(M), il admet un générateur g. L'élément pi est dans l'idéal PA(M) ce qui montre l'existence d'élément ai de A et bi de A - M tel que pi = gaibi−1. Soit b le produit des éléments bi, c'est un élément de A - M, et baix−1 est un élément de A, ce qui montre que bx−1 est un élément de F et b est élément de F.P.A(M). Ceci montre que b est élément de M.A(M). b est un élément de A et de M.A(M), on en déduit qu'il est élément de M. Or b n'est pas élément de M, cette contradiction démontre que P.F est égal à A, donc que tout idéal premier est inversible et par voie de conséquence, que A est de Dedekind.

 

Extension finie

Article détaillé : Extension algébrique.

Une méthode pour construire un anneau de Dedekind est de considérer la fermeture algébrique d'un corps des fractions K d'un anneau de Dedekind A.

La séparabilité de L est utilisée pour montrer l'aspect noethérien de B. La forme trace de l'anneau B est non dégénérée, ce qui permet de montrer simplement le caractère noethérien de B. Le corps L joue un rôle particulier vis à vis de B :

  • Le corps des fractions de B est égal à L.

L'étude des anneaux de Dedekind d'une extension de cette nature offre des outils d'analyse de la structure du corps L. La décomposition des idéaux premiers de K dans L permet de définir la ramification. Ce concept est utilisé, par exemple pour établir le théorème de Kronecker-Weber. La théorie des corps de classes généralise son usage.

Démonstrations
  • L'ensemble B est un anneau commutatif unitaire et intègre :

L'ensemble B est un sous-ensemble non vide de L contenant A, il suffit de montrer la stabilité de B pour l'addition, la soustraction et la multiplication. Une démonstration de ces stabilités est donnée dans l'article Polynôme minimal d'un nombre algébrique. L'anneau B est commutatif et intègre car L l'est. Enfin B est unitaire car il contient A.

  • Le corps des fractions de B est égal à L.

Le corps L contient B, il contient en conséquence son corps des fractions. Réciproquement montrons que tout élément l de L est élément du corps des fractions de B. L'élément l admet un polynôme minimal, en multipliant ce polynôme par le produit des dénominateurs des coefficients du polynôme on obtient :

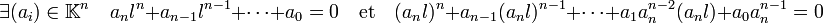
\exists (a_i) \in \mathbb K^n\quad a_nl^n + a_{n-1}l^{n-1} + \cdots + a_0 = 0 \quad \text{et}\quad (a_nl)^n + a_{n-1}(a_nl)^{n - 1} + \cdots + a_1a_n^{n-2}(a_nl) + a_0a_n^{n-1}=0\;

Notons u = anl, l'égalité précédente montre que u est entier sur A donc élément de B et l est égal à u.an−1, ce qui montre que l est élément du corps des fractions de A et termine la démonstration.

  • L'anneau B est intégralement clos :

Il s'agit de montrer que tout élément de L ayant un polynôme minimal à coefficient dans B est élément de B. Soit l un entier algébrique de L, Soit (bi) les différents coefficients du polynôme minimal. La plus petite A algèbre de L contenant (bi) et l est de type fini, cette propriété montre que l est entier sur A. La démonstration est donnée dans l'article Polynôme minimal d'un nombre algébrique.

  • L'anneau B est noethérien :

Une démonstration est proposée dans l'article Anneau noethérien.

  • Tout idéal premier de B est maximal :

Soit P un idéal premier de B et M un idéal maximal contenant P. On raisonne par l'absurde et l'on suppose qu'il existe un élément m de M qui ne soit pas élément de P.

Notons PA (resp. MA) l'intersection de P (resp. M) avec A. Les idéaux PA et MA sont premiers, et MA contient PA, comme l'anneau A est de Dedekind ces deux idéaux sont égaux. Soit P[X] un polynôme unitaire à coefficients dans A de plus petit degré tel que P[m] soit un élément de P. L'ensemble des polynômes unitaires à coefficients dans A tel que l'image de m soit dans P est non vide, il contient au moins le polynôme minimal. Comme m n'est pas dans P, il n'est pas dans A et P[X] n'est pas de degré un. On utilise les notations :

P[X] = X^n + a_{n-1}X^{n-1} + \cdots + a_0 \quad\text{et}\quad p = a_nm^n + a_{n-1}m^{n-1} + \cdots +a_1m \;

La valeur P[m] est égal à p + a0. Les valeurs p et P[m] sont dans M, ce qui montre que a0 est aussi dans M. On en déduit que a0 est à la fois dans M et dans A et donc dans PA. Ce qui montre que le polynôme Q[X], définit par :

P[X] = X^{n-1} + a_{n-1}X^{n-2} + \cdots + a_1\;

vérifie aussi le fait que Q[m] soit élément de P, ce qui contredit la minimalité du degré de P[X]. Cette contradiction permet de conclure.

  • Conclusion :

L'anneau B est commutatif, unitaire, intègre et noethérien. Il est intégralement clôt, son corps des fractions est L et tout idéal premier de B est maximal. On a bien montré que l'anneau B est de Dedekind.

 

Notes et références

Notes

  1. ↑ a  et b  Richard Dedekind Zur Theorie der Ideale Nachr der K. Ges. Der Wiss. zu Göttingen 1894
  2. ↑ est celle utilisée dans les références du paragraphe et aussi celle du site Dimatu Dictionnaire Mathématiques Universel. Elle n'est pas à confondre avec celle de fermeture algébrique
  3. ↑ Cette définition est celle utilisée dans les références du paragraphe et aussi celle du site Dimatu Dictionnaire Mathématiques Universel
  4. ↑ Les définitions de se paragraphe proviennent par exemple du site Théorie algébrique des nombres Un cours de maîtrise de mathématiques par B. Edixhoven, Université de Rennes 1. Les mêmes définitions sont utilisées dans la référence Pierre Samuel, Théorie algébrique des nombres [détail des éditions]
  5. ↑ H. M. Edwards Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory Springer 3ème Ed 2000 (ISBN 0387950028)
  6. ↑ Carl Friedrich Gauss Recherches arithmétiques trad. française des Disquisitiones arithmeticae par A.-C.-M. Poullet-Delisle 1801 lire
  7. ↑ Dirichlet Démonstration du théorème de Fermat et de Wilson (compte-rendu par Cournot de quelques mémoires d'Abel, Jacobi et Lejeune-Dirichlet, au Journ. der Mathemat., de M. Crelle, t. 3, cah. 4). 1829, t. 11, p. 153-157
  8. ↑ Dirichlet Vorlesungen über Zahlentheorie publié par R. Dedekind Braunschweig Viweg und Sohn 1863
  9. ↑ On trouve une description de la preuve sur le site Fermat's last theorem
  10. ↑ Gabriel Lamé Démonstration générale du théorème de Fermat, sur l'impossibilité, en nombres entiers, de l'équation xn +yn =zn Comptes Rendus des Séances de l'Académie des Sciences. Paris 1847 24, 310-315 Lire sur Gallica
  11. ↑ H.M. Edwards, The background of Kummer's proof of Fermat's Last Theorem for regular primes, Arch. History Exact Sci. 14(1975)
  12. ↑ Cette expression est par exemple utilisé p 27 dans le site suivant : Théorie algébrique des nombres Un cours de maîtrise de mathématiques par B. Edixhoven, Université de Rennes 1
  13. ↑ Ernst Kummer Beweis des Fermat'schen Satzes der Unmöglichkeit von xλ+yλ=zλ für eine unendliche Anzahl Primzahlen λ Monatsber, Akad. d. Wiss. Berlin pp 132-139, 140-141, 305-319 1847
  14. ↑ Richard Dedekind Sur la théorie des nombres entiers algébrique Gauthier-Villars Paris, 1877
  15. ↑ La définition est donnée dans ses commentaires de son réédition de ; Dirichlet Vorlesungen über Zahlentheorie publié par R. Dedekind Braunschweig Viweg und Sohn 1871
  16. ↑ Richard Dedekind Traité sur la théorie des nombres trad. C. Duverney, Tricorne, Genève, 2006 (ISBN 2829302893)
  17. ↑ Ce paragraphe provient du texte Dedekind's 1871 version of the theory of ideals traduit en anglais par J. Avigad en 2004
  18. ↑ Cette comparaison vient du site suivant, en page I-6 Nombres algébriques et nombres p-adiques par Loïc Merel cours préparatoire aux études doctorales 2003-04

Liens externes

Références

  • (fr) Pierre Samuel, Théorie algébrique des nombres [détail des éditions]
  • (fr) Jean-Pierre Serre, Cours d'arithmétique [détail des éditions]
  • (fr) N. Bourbaki Éléments de mathématiques, Algèbre commutative chap 8 et 9 Masson 1983 (ISBN 2225787166)
  • (en) G. H. Hardy E. M. Wright An Introduction to the Theory of Numbers Oxford Science Publications 1980 (ISBN 0198531710)
  • (en) K. Ireland M. Rosen A Classical Introduction to Modern Number Theory Springer; 2nd ed. 1990. Corr. 5ième édition imprimée 1998 (ISBN 038797329X)
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Anneau de Dedekind ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Anneau De Dedekind de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Anneau de dedekind — Richard Dedekind définit et établit les bases de la théorie des anneaux portant maintenant son nom. En mathématiques, un anneau de Dedekind est un anneau disposant de propriétés particulières. Sa formalisation initiale a pour objectif la… …   Wikipédia en Français

  • Anneau de Dedekind — Richard Dedekind définit et établit les bases de la théorie des anneaux portant maintenant son nom. En mathématiques, un anneau de Dedekind est un anneau commutatif disposant de propriétés particulières. Sa formalisation initiale a pour objectif… …   Wikipédia en Français

  • Anneau Principal — Les anneaux principaux forment un type d anneaux important dans la théorie mathématique de la divisibilité. Ce sont les anneaux intègres (commutatifs unitaires non nuls) auxquels on peut étendre deux théorèmes qui, au sens strict, concernent l… …   Wikipédia en Français

  • Anneau (Mathématiques) — Pour les articles homonymes, voir Anneau. En algèbre générale, un anneau est une structure algébrique sur laquelle deux opérations satisfont certaines des propriétés de l addition et la multiplication des nombres. Sommaire 1 Aspect historique …   Wikipédia en Français

  • Anneau Noethérien — Emmy Noether formalise les propriétés d une famille particulière d anneaux maintenant appelé anneau noethérien. En mathématique, un anneau noethérien est un cas particulier d anneau, c est à dire d un ensemble munis d une addition et d une… …   Wikipédia en Français

  • Anneau noetherien — Anneau noethérien Emmy Noether formalise les propriétés d une famille particulière d anneaux maintenant appelé anneau noethérien. En mathématique, un anneau noethérien est un cas particulier d anneau, c est à dire d un ensemble munis d une… …   Wikipédia en Français

  • Anneau Factoriel — En mathématiques, un anneau factoriel est un cas particulier d anneau commutatif, unitaire et intègre. À l image des nombres entiers, il existe un équivalent du théorème fondamental de l arithmétique pour une telle structure. Tout élément d un… …   Wikipédia en Français

  • Anneau a valuation discrete — Anneau à valuation discrète En mathématiques, un anneau à valuation discrète est un cas particulier d anneau intègre. Il dispose d une structure particulièrement simple puisqu il ne contient qu un unique idéal maximal et qu il est principal. Il… …   Wikipédia en Français

  • Anneau À Valuation Discrète — En mathématiques, un anneau à valuation discrète est un cas particulier d anneau intègre. Il dispose d une structure particulièrement simple puisqu il ne contient qu un unique idéal maximal et qu il est principal. Il est utilisé en théorie… …   Wikipédia en Français

  • Anneau à valuation discrète — En mathématiques, un anneau à valuation discrète est un cas particulier d anneau intègre. Il dispose d une structure particulièrement simple puisqu il ne contient qu un unique idéal maximal et qu il est principal. Il est utilisé en théorie… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”