Extension Abélienne

Extension Abélienne: Extension abélienne

Introduction

En algèbre générale, plus précisément en théorie de Galois, une extension abélienne est une extension de corps dont le groupe de Galois associé est abélien. Lorsque le groupe de Galois est un groupe cyclique, nous avons une extension cyclique.

Toute extension finie d'un corps fini est une extension cyclique. L'étude de la théorie des corps de classes décrit de façon détaillée toutes les extensions abéliennes dans le cas des corps de nombres, et des corps de fonctions de courbes algébriques sur des corps finis, ainsi que dans le cas des corps locaux (théorie locale du corps de classes).

Cyclotomie et Extensions abéliennes au dessus des nombres rationnels

Les extensions cyclotomiques, obtenues par l'adjonction de racines de l'unité donnent des exemples d'extensions abéliennes au dessus de n'importe quel corps. Ces extensions peuvent être triviales si le corps duquel on part est Corps algébriquement clos ou bien si l'on adjoint des racines 'p'mes en caractéristique 'p'.

Dans le cas où le corps de corps de base est le corps Q des nombres rationnels, on obtient par cette constructions les dits corps cyclotomiques. Le corps Q(i) des nombres de Gauss a+bi, pour a et b rationnels, en est l'exemple non trivial le plus simple. Les corps cyclotomiques sont les exemples essentiels d'extension abélienne de Q, au sens où toute extension abélienne se plonge dans un tel corps.

Ainsi une extension abélienne maximale Q^ab de Q s'obtient en adjoignant toutes les racines de l'unité à Q. C'est un cas particulier de la théorie du corps de classes local au cas du corps Q. Dans ce cas le groupe de Galois de l'extension de Q^ab au dessus de Q s'identifie au groupe 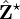$\hat{\mathbf{Z}}^\star$ des éléments inversibles de 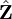$\hat{\mathbf{Z}}$ . Il agit sur les racines primitives Nmes de l'unité par l'intermédiaire de son quotient 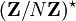$(\mathbf{Z}/N\mathbf{Z})^\star$ , où k+NZ agit en envoyant la racine $ζ$ sur $ζ k$ .

Multiplication complexe et Jügendtraum

Dans le cas du corps Q il est remarquable qu'une extension abélienne maximale est engendrée par des valeurs spéciales de la fonction exponentielle. En effet, parmi les nombres complexes, les racines de l'unité se distinguent comme celles qui s'écrivent $exp(2π i * x)$ pour les valeurs rationnelles du paramètre x. Ces paramètre sont les seuls nombres algébriques auxquels la transcendante $exp(2π i * x)$ prend des valeurs algébriques (une racine Nme satisfait l'équation X^N=1), d'où le nom de valeur spéciale.

Dans le cas de corps de nombres quadratiques complexes, il faut rajouter aux racines de l'unité les nombres algébriques obtenues à partir des coordonnées des points de torsion d'une courbe elliptique. C'est la théorie de la multiplication complexe. Ces considérations s'inscrivent dans le Jügendtraum de Kronecker.

Ce document provient de « Extension ab%C3%A9lienne ».

Catégorie : Théorie de Galois

Contenu soumis à la licence CC-BY-SA. Source : Article Extension Abélienne de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Extension abelienne — Extension abélienne Introduction En algèbre générale, plus précisément en théorie de Galois, une extension abélienne est une extension de corps dont le groupe de Galois associé est abélien. Lorsque le groupe de Galois est un groupe cyclique, nous … Wikipédia en Français
Extension abélienne — En algèbre générale, plus précisément en théorie de Galois, une extension abélienne est une extension de corps dont le groupe de Galois associé est abélien. Lorsque le groupe de Galois est un groupe cyclique, nous avons une extension cyclique.… … Wikipédia en Français
Extension Cyclotomique — En théorie algébrique des nombres, on appelle extension cyclotomique du corps des nombres rationnels, les surcorps de la forme où ζn est une racine primitive nème de l unité ; cette appellation provient de ce que ces extensions sont des… … Wikipédia en Français
Extension cyclotomique — En théorie algébrique des nombres, on appelle extension cyclotomique du corps Q des nombres rationnels tout corps de rupture d un polynôme cyclotomique, i.e. tout corps de la forme Q(ζ) où ζ est une racine de l unité. Ces corps jouent un rôle… … Wikipédia en Français
Extension de Kummer — Théorie de Kummer En mathématiques, la théorie de Kummer, ainsi désignée suivant le nom du mathématicien allemand du XIX siècle Ernst Kummer, suite à ses travaux sur le dernier théorème de Fermat, donne une description de certaines extensions d… … Wikipédia en Français
Extension décomposée — Décomposition des idéaux premiers En théorie algébrique des nombres, le théorème fondamental de l arithmétique, valable sur les entiers relatifs, peut ne plus être vrai si on considère des entiers algébriques à la place. Toutefois, le théorie des … Wikipédia en Français
Extension ramifiée — Décomposition des idéaux premiers En théorie algébrique des nombres, le théorème fondamental de l arithmétique, valable sur les entiers relatifs, peut ne plus être vrai si on considère des entiers algébriques à la place. Toutefois, le théorie des … Wikipédia en Français
Extension Quadratique — En mathématiques, et plus précisément en algèbre dans le cadre de la théorie de Galois, une extension quadratique est une extension de corps de dimension deux. Si K est un corps commutatif, souvent celui des nombres rationnels, alors une… … Wikipédia en Français
Extension quadratique — En mathématiques, et plus précisément en algèbre dans le cadre de la théorie de Galois, une extension quadratique est une extension de corps de dimension deux. Si K est un corps commutatif, souvent celui des nombres rationnels, alors une… … Wikipédia en Français
Extension radicielle — Dans la théorie des extensions de corps, à l opposé des extensions algébriques séparables, il existe les extensions radicielles. C est un phénomène spécifique à la caractéristique positive et qui apparaît naturellement avec les corps de fonctions … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Extension Abélienne

Extension abélienne

Introduction

Cyclotomie et Extensions abéliennes au dessus des nombres rationnels

Multiplication complexe et Jügendtraum

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Extension Abélienne

Extension abélienne

Introduction

Cyclotomie et Extensions abéliennes au dessus des nombres rationnels

Multiplication complexe et Jügendtraum

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link