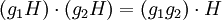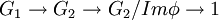Groupe Quotient

Groupe quotient

Dans l'étude des groupes, le quotient d'un groupe est une opération classique permettant la construction de nouveaux groupes à partir d'anciens. À partir d'un groupe G et d'un sous-groupe H de G, on peut définir une loi de groupe sur l'ensemble G/H des classes de G suivant H, à condition que H soit stable par les automorphismes intérieurs de G , c'est-à-dire que les classes latérales droites soient égales aux classes latérales gauches (gH = Hg). Un tel sous-groupe est appelé sous-groupe normal ou sous-groupe distingué.

Sommaire

1 Partition d'un groupe en classes modulo un sous-groupe
2 Définition
3 Exemples
4 Propriétés
- 4.1 Factorisation des morphismes
5 Voir aussi
- 5.1 Articles connexes
- 5.2 Lien externe

Partition d'un groupe en classes modulo un sous-groupe

Étant donné un élément 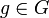$g \in G$ , nous définissons la classe à gauche 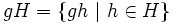$g H = \{ g h\ |\ h \in H \}$ . Comme $g$ est inversible, l'ensemble $g H$ a le même cardinal que $H$ . De plus, tout élément de $G$ appartient à exactement une seule classe à gauche de $H$ ; l'ensemble des classes à gauche sont des classes d'équivalence correspondant aux classes d'équivalence de la relation d'équivalence définie par g₁ ~ g₂ si et seulement si 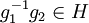$g_{1}^{-1} g_2 \in H$ . Le nombre de classes à gauche de $H$ est appelé l'indice de $H$ dans $G$ et est noté $[G : H]$ . Dans le cas d'un groupe fini, le théorème de Lagrange sur la cardinalité des sous-groupes, et la formule des classes permettent de voir que cet indice est fini et est un diviseur de l'ordre du groupe G.

Les classes à droite sont définies de manière analogue: 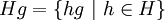$Hg = \{ h g\ |\ h \in H \}$ . Elles sont aussi les classes d'équivalence pour une relation d'équivalence convenable et leur cardinal est égal à $[G : H]$ .

Définition

Si pour tout 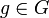$g \in G$ , $g H = H g$ , alors $H$ est appelé un sous-groupe distingué ou normal ou invariant. Dans ce cas, nous définissons une multiplication sur les classes par

$(g_1 H) \cdot (g_2 H) = (g_1 g_2) \cdot H$

Cela donne à l'ensemble des classes une structure de groupe ; ce groupe est appelé groupe quotient (ou parfois groupe des facteurs) noté $G / H$ . L'application 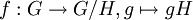$f : G \rightarrow G/H, g \mapsto gH$ est alors un homomorphisme de groupe. L'image directe $f (H)$ n'est constituée que de l'élément neutre de $G / H$ , à savoir la classe $e H = H$ . L'application f est appelé morphisme canonique.

Exemples

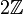Considérons l'ensemble des entiers relatifs $\mathbb{Z}$ et le sous-groupe $2\mathbb{Z}$ constitué des entiers pairs. Alors le groupe quotient 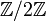$\mathbb{Z}/2\mathbb{Z}$ est constitué de deux éléments, représentant la classe des nombres pairs et la classe des nombres impairs.
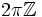L'ensemble $\mathbb{R}$ des nombres réels, considéré comme groupe additif, et son sous-groupe $2\pi\mathbb{Z}$ permettent de définir un groupe quotient utilisé pour la mesure des angles orientés.

Propriétés

$G / G$ est isomorphe au groupe trivial, c'est-à-dire réduit à l'élément neutre.
Si $H$ est distingué, l'application 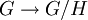$G \rightarrow G/H$ est un morphisme surjectif, appelé projection canonique, de noyau $H$ .
Plus généralement, si 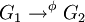$G_1\rightarrow^\phi G_2$ est un morphisme de groupes, il existe une suite exacte :

$G_1\to G_2\to G_2/Im\phi\to 1$

Si $G$ est abélien, cyclique, nilpotent ou résoluble, il en sera de même pour $G / H$ .

Factorisation des morphismes

Article détaillé : Théorèmes d'isomorphisme.

On peut caractériser les groupes quotients par la propriété fondamentale suivante :

Soit 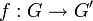$f : G \rightarrow G'$ un morphisme de groupe. Soit

H

le noyau de

f

. Alors H est distingué et

f

se « factorise » en un morphisme injectif 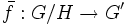$\bar f : G/H \to G'$ tel que 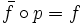$\bar f\circ p = f$ , où p est la projection de

G

sur

G / H

Voir aussi

Lien externe

congruence modulo un sous-groupe

Portail des mathématiques

Ce document provient de « Groupe quotient ».

Catégorie : Théorie des groupes

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Groupe Quotient de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires: