- Extension Quadratique
-
Extension quadratique
En mathématiques, et plus précisément en algèbre dans le cadre de la théorie de Galois, une extension quadratique est une extension de corps de dimension deux. Si K est un corps commutatif, souvent celui des nombres rationnels, alors une extension quadratique L est un corps contenant K et un espace vectoriel sur K de dimension deux.
Une extension quadratique est le cas le plus simple d'extension de corps. Elle possède de nombreuses propriétés, c'est une extension simple algébrique et un corps de décomposition si le corps n'est pas de caractéristique deux. L'extension est séparable, normale et donc galoisienne et même abélienne.
La notion d'extension quadratique possèdent de nombreuses applications, on peut citer la Théorie de Kummer ou la notion de tour d'extension quadratique utilisée pour la démonstration du Théorème de Gauss-Wantzel ou la résolution de l'équation cyclotomique dans le cas où d'une racine primitive n-ième de l'unité où n est un nombre premier de Fermat.
Sommaire
Motivations
Une extension quadratique correspond au cas le plus simple d'extension algébrique. Il correspond au cas où l'extension est réalisée à partir d'un unique élément dont le carré est combinaison de lui-même et d'un élément du corps de base.
De plus, à la condition que le corps soit commutatif et ne soit pas de caractéristique 2, c’est-à-dire si la somme de l'unité avec lui-même n'est pas égale à zéro, alors une telle extension possède toutes les bonnes propriétés des extensions de Galois. Il est possible d'établir tous les résultats principaux de la théorie avec des démonstrations largement plus simples. Cette théorie dépasse donc le cadre des extensions sur le corps des nombres rationnels ou réels.
Une première application a été trouvé par Carl Friedrich Gauss (1777 1855) en 1801 pour l'étude des polygones constructible à la règle et au compas. Les propriétés des extensions quadratiques permettent de déterminer un algorithme pour chaque polygone constructible (cf Polynôme cyclotomique). Les propriétés des extensions quadratiques sont utilisées alors dans un cas particulier, celui de la tour d'extension quadratique.
Cette théorie possède de plus de nombreuses applications en théorie des nombres comme par exemple la théorie de Kummer. Dans ce domaine, il existe encore des problèmes ouverts qui font l'objet de recherche.
Dans la suite de l'article le corps de base est noté K, il ne possède que deux propriétés spécifiques, il est commutatif et sauf indication contraire, il n'est pas de caractéristique deux.
Définition
-
- Soit K un corps, L une extension de corps de K. L'extension L est dite quadratique si et seulement si la dimension de L comme espace vectoriel sur K est égal à deux. Si α est un élément de L qui n'est pas élément de K, alors l'extension est souvent noté K(α).
-
- Un élément d'une extension L sur K est dit quadratique s'il est inclus dans une extension quadratique de K.
Remarque: K(α) désigne le plus petit corps contenant α, il est donc engendré par les puissances de α. Dans le cas d'une extension quadratique, tout élément de L est combinaison linéaire de 1 et α, car l'espace est de dimension deux et que 1 et α forment une famille libre car α n'est pas élément de K.
Remarque: Toute extension de corps est un espace vectoriel sur son corps de base. Cette propriété n'est pas spécifique aux extensions quadratiques.'
Exemples
- L'exemple le plus connu est probablement l'extension quadratique des nombres réels égale au corps des nombres complexes.
- L'ensemble des combinaisons linéaires de l'unité et √2 sur le corps des nombres rationnels est une extension quadratique. Cet exemple est étudié dans l'article sur les extensions algébriques.
- Soit F3 le corps Z/3Z. Considérons le polynôme formel P(X)= X 2 + 1. Un polynôme formel est un polynôme construit non pas à l'aide d'une variable, mais d'une indéterminée. Dans F3 les fonctions polynômes x3 et x sont confondues, les polynômes formels X3 et X ne le sont pas par définition. Il est aisé de vérifier que ce polynôme n'admet pas de racine dans F3. En effet, les classes de 1 et de 2 ont pour carré 1, et 0 a pour carré 0, le polynôme est donc irréductible. Considérons le quotient de l'anneau des polynômes F3[X] avec son idéal engendré par P[X]. C'est un anneau, cet anneau est non seulement un corps fini mais aussi une extension quadratique de F3. Pour le vérifier il suffit de vérifier que l'idéal engendrée par P(X) est maximal. Comme F3 est un corps, F3[X] est un anneau euclidien donc principal. Pour ce type d'anneau, un idéal est maximal si et seulement s'il est idéal premier, or tout idéal engendré par un élément irréductible est premier si l'anneau est principal. Cette technique permet de construire un corps à neuf éléments.
Construction d'une extension quadratique
Cas général
Soit d un élément de K tel qu'il n'existe aucun élément de K dont le carré est égal à d. Le polynôme P(X) égal à X2 - d n'admet pas de racine et est donc irréductible dans K. Un raisonnement analogue à celui du troisième exemple montre que le quotient K[X]/P(X) de l'espace des polynômes par l'idéal engendré par P(X) est un corps, noté ici L. Soit Q(X) un polynôme à coefficients dans K, la division euclidienne de Q(X) par P(X) montre qu'il est congru à un polynôme du premier degré. Tout élément de L admet donc comme représentant un polynôme du premier degré. Un exemple de cette nature est donnée dans l'article Indéterminée.
L'application de K dans L qui à k associe sa classe est un plongement de K dans L, c'est-à-dire un morphisme injectif de corps. Il est donc possible d'identifier K avec une partie de L, celle des classes de K. Si la classe du monôme X est noté √d, alors tout élément de L est combinaison linéaire de 1 et de √d, car tout élément de L possède pour représentant un polynôme de degré 1. Pour cette raison, l'extension est souvent noté K(√d). L est un K espace vectoriel engendré par une famille de deux éléments, 1 et √d, cette famille est libre car, par hypothèse √d n'est pas un élément de K. Le corps L est bien une extension quadratique de K.
Réciproquement, soit M une extension quadratique quelconque de K. Soit z un élément de M qui n'est pas élément de K. La famille (1, z) est une base de M, en tant que K espace vectoriel, car elle est libre et de cardinal égal à la dimension de l'espace. L'élément z2 est combinaison linéaire de 1 et de z et il existe -b et -c deux élément de K tel que : z2 + b.z + c est égal à 0. On en déduit l'égalité :
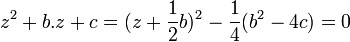
Comme K n'est pas de caractéristique 2, 2 et 4 sont bien des éléments différents de 0 donc inversibles. Notons d la valeur (b2 - 4.c)/4. Le fait que b et c soit éléments de K montre que d l'est aussi. Soit δ l'élément de M égal à z + b/2, on remarque que δ n'est pas élément de K car z ne l'est pas et δ2 est égal à d. On en déduit que d n'a pas de racine dans K.
Le polynôme P(X) = X2 - d est irréductible. Considérons alors L le quotient K[X]/P(X). Pour les mêmes raisons que précédemment, L est un corps, noté K(√d). Un calcul élémentaire montre qu'il existe un automorphisme de corps de M dans L qui à δ associe √d. Ce qui montre la proposition suivante :
-
- Soit L une extension quadratique de K, il existe un élément d de K qui n'admet pas de racine carrée dans K tel que L est isomorphe à K(√d).
Cas des rationnels
Un cas souvent utilisé en arithmétique est celui où K est égal à Q, l'ensemble des rationnels. La propriété précédente prend une forme un peu plus forte :
-
- Soit L une extension quadratique de Q, il existe un unique entier d sans facteur carré tel que L est égal à Q(√d).
Un entier est dit sans facteur carré si sa décomposition en facteurs premiers ne comporte que des exposants égaux à un.
- Remarque : Le symbole √ porte une double signification. Soit il désigne une fonction des réels positifs vers les réels positifs, soit il désigne la classe de X dans le quotient défini précédemment. La première définition ne peut se généraliser aux nombres négatifs. En effet, √-1 n'a pas de racine dans R, l'ensemble des réels et en possède deux dans celui des complexes. Si l'approche algébrique permet de définir rigoureusement √-1, tel n'est pas le cas de la deuxième. Pour cette raison, si d est strictement positif, √-d est aussi noté i√d, avec i désignant l'unité imaginaire. L'extension est alors identifiée avec un sous-corps des nombres complexes.
Démonstration-
- Existence :
Soit deux entiers p et q tel que p/q est égal à d. Il est possible de multiplier d est aussi égal à p.q /q2, en conséquence, Q(√d) est égal à Q(√p.q) et toute extension quadratique de Q s'exprime comme une extension d'un radical entier.
L'entier p.q s'exprime comme le produit de deux facteurs, l'un contenant tous les facteurs carrés et l'autre sans facteur carré. Il existe ainsi deux entiers n et m tel que p.q = n2.m. On remarque alors que Q(√d) est égal à Q(√n) et l'entier n ne contient aucun facteur carré.
-
- Unicité :
Soit d1 et d2 deux entiers sans facteur carré, tel que les deux extensions soient confondues. Alors :
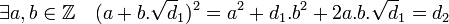
On en déduit que 2.a.b est égal à 0 et a2 + d1.b2 = d2. L'entier b ne peut être nul, d2 serait alors un carré. En conséquence a est nul et comme d2 ne contient aucun facteur carré b est égal à 1 donc d1 est égal à d2. Ce qui montre l'unicité.
Propriétés galoisiennes
Dans ce paragraphe L désigne une extension quadratique du corps K de caractéristique différente de 2.
Séparation
Article détaillé : Extension séparable.-
- L'extension L est séparable.
Si dans un corps, on additionne plusieurs fois de suite l'unité, il est possible de trouver zéro. C'est par exemple toujours le cas si le corps est de cardinal fini. Dans le cas où les sommes successives de l'unité ne sont jamais nulles alors on parle de caractéristique nulle. C'est par exemple le cas pour les corps des nombres rationnels, réels ou complexes.
Dire que l'extension L est séparable, c'est dire que les polynômes minimaux n'ont jamais de racines multiples. Cette propriété est importante pour la théorie de Galois. Elle apparaît dans la suite de l'analyse des propriétés des extensions quadratiques. Soit l un élément de L et P[X] son polynôme minimal à coefficient dans K. On suppose que l n'est pas élément de K car sinon son polynôme est de degré 1 est il n'existe évidemment pas de racine multiple. Alors P[X] est de degré deux. Sa dérivée est de degré un à coefficient dans K car P[X] est à coefficients dans K. Comme l n'est pas élément de K, l ne peut être racine de la dérivée. Or une racine est multiple si et seulement si elle est aussi racine du polynôme dérivée.
Ce raisonnement ne s'applique pas en caractéristique deux. considérons en effet un polynôme de la forme X2 - c, ou c est un élément de K, sa dérivé est toujours nulle donc toute racine carrée possède un polynôme minimal non séparable.
Groupe de Galois
Article détaillé : Extension de Galois.Le groupe de Galois est le groupe des automorphismes de corps de L laissant K invariant. Si l'extension est séparable, elle est dite de Galois si et seulement si elle est aussi extension normale, c'est-à-dire si tout morphisme de corps de L dans une clôture algébrique a pour image L. Une clôture algébrique est une extension de K tel que tout polynôme à coefficients dans la clôture admet au moins une racine. Par exemple, le corps des complexes est une clôture algébrique des nombres réels. On démontre d'ailleurs que c'est la seule (cf la preuve par la théorie de Galois du théorème de d'Alembert-Gauss). Une propriété démontrée dans l'article détaillé montre qu'une extension séparable L est galoisienne si et seulement si le groupe de Galois contient autant d'élément que la dimension de L sur K.
-
- Il existe exactement deux automorphismes de corps de l'extension quadratique L, laissant K invariant.
En effet, soit d un élément de K tel que L est égal à K[√d] et σ un automorphisme de L différent de l'identité et laissant invariant K. Pour tout élément de K L'application σ est aussi un automorphisme de K espace vectoriel. Par définition σ laisse K stable donc l'image de d est égal à d. On en déduit que σ (√d2) égal à σ (√d)2 est égal à d et donc σ (√d) est égal à + ou - √d.
La famille (1, √d) est une base du K espace vectoriel L, l'image de 1 par σ est égal à 1 car K est stable par σ et 1 est élément de K. Le fait que σ est différent de l'identité montre que σ (√d) est égal à -√d. On en déduit que σ est défini par :
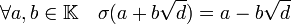
-
- L'automorphisme σ, laissant invariant K et tel que l'image de √d est égal à -√d est appelée application conjugué de L sur K.
On vérifie que l'application définie par l'égalité précédente est bien un automorphisme de corps.
-
- L'extension L sur K est normale, galoisienne et abélienne.
En effet, le groupe de Galois de l'extension L sur K contient deux éléments, l'identité et σ . Une proposition démontrée dans l'article détaillée montre que toute extension séparable dont le groupe de Galois contient autant d'éléments que la dimension de L sur K est normale et galoisienne. Le groupe de Galois contient deux éléments, il est donc abélien et l'extension L est abélienne.
Corps quadratique et corps cyclotomique
Il existe un unique corps quadratique inclus dans le corps cyclotomique engendré par une racine primitive p-ième de l'unité, avec p, un nombre premier impair : en effet, le corps cyclotomique est une extension cyclique du corps des rationnels, de degré pair p-1, et la théorie de Galois assure l'existence et l'unicité souhaitées. Le discriminant du corps quadratique est p pour
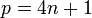 et - p pour
et - p pour 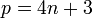 : en effet, les seules places ramifiées dans le corps cyclotomique sont la place p et la place à l'infini, ce sont donc les seules susceptibles de se ramifier dans le corps quadratique, et, comme noté ci-dessus, tout nombre premier divisant le discriminant réduit d'un corps quadratique est ramifié dans ce corps.
: en effet, les seules places ramifiées dans le corps cyclotomique sont la place p et la place à l'infini, ce sont donc les seules susceptibles de se ramifier dans le corps quadratique, et, comme noté ci-dessus, tout nombre premier divisant le discriminant réduit d'un corps quadratique est ramifié dans ce corps.Un corps cyclotomique engendré par une racine n-ème de l'unité, pour n non premier admettent en revanche par la théorie de Galois plusieurs sous-corps quadratiques (non cyclicité du groupe de Galois).
Entier quadratique
Article détaillé : Entier quadratique.Un des intérêts des extensions quadratiques est la résolution d'équations diophantiennes. Celles du grand théorème de Fermat, de Pell-Fermat ou des deux carrés en sont des exemples. Une partie uniquement de l'extension est considérée, celles des entiers algébriques. Soit d est un entier sans facteur carré, un élément u de Q(√d) est dit entier si et seulement s'il existe un polynôme unitaire et à coefficients entiers admettant u pour racine.
- Portail des mathématiques
Catégories : Théorie de Galois | Entier quadratique -
Wikimedia Foundation. 2010.
