- Theoreme fondamental de l'arithmetique
-
Théorème fondamental de l'arithmétique
En mathématiques, et en particulier en arithmétique élémentaire, le théorème fondamental de l'arithmétique ou théorème de décomposition en produit de facteurs premiers ou théorème de factorisation unique s'énonce ainsi:
Théorème fondamental de l'arithmétique — Chaque entier strictement positif peut être écrit comme un produit de nombres premiers d'une unique façon, à l'ordre près des facteurs.
Par exemple, nous pouvons écrire
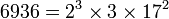ou encore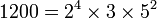 
et il n'existe aucune autre factorisation de 6936 ou 1200 sous forme de produits de nombres premiers, excepté par réarrangement des facteurs ci-dessus.
Le nombre 1 est le produit de zéro nombre premier (voir produit vide), de sorte que le théorème est aussi vrai pour 1.
Ce résultat se généralise sur d'autres ensembles comme les anneaux factoriels ou les polynômes à coefficients dans les nombres réels ou complexes (cf arithmétique des polynômes).
Sommaire
Histoire
Dans le livre VII de ses Éléments, Euclide énonce que tout nombre non premier est divisible par un nombre premier[1]. Cette proposition plus faible que le théorème fondamental de l'arithmétique, est suffisante pour certaines applications. Le résultat était déjà connu et utilisé par des civilisations antérieures[réf. nécessaire].
Gauss
En 1801 dans son livre Recherches arithmétiques, Carl Friedrich Gauss (1777-1855) développe des arithmétiques sur d'autres structures[réf. nécessaire]. L'existence d'une factorisation est étendue aux entiers relatifs, aux polynômes à coefficients dans un corps ainsi qu'à un nouvel anneau d'entiers algébriques, les entiers de Gauss. La notion de nombre premier est alors étendue. Elle s'applique de la même manière pour les polynômes irréductibles ou les nombres premiers de Gauss. Dans tous ces cas, la décomposition est complétée par un facteur correspondant à un élément inversible. Dans le cas des entiers relatifs le facteur est égal à (+ 1) si le nombre est positif et (- 1) s'il est négatif.
La décomposition est encore généralisée à toute une classe d'anneaux : les anneaux factoriels[réf. nécessaire].
Démonstration
La démonstration est constituée de deux parties : premièrement, nous avons à montrer que (1) chaque nombre peut vraiment être écrit comme un produit de nombres premiers ; puis nous avons à montrer que (2) deux représentations d'un même nombre sont essentiellement les mêmes.
(1) Existence
La preuve de l'existence s'appuie sur le principe de récurrence ou une propriété équivalente (que l'ensemble des entiers naturels vérifie par construction).
Raisonnement par récurrence :
- 1 est le produit d'une famille vide de nombres premiers ;
- Supposons que tout entier inférieur à un entier n est produit d'une famille de nombres premiers. Deux possibilités apparaissent pour n :
- Soit n est premier, et donc produit d'un unique entier premier, à savoir lui-même et le résultat est vrai.
- Soit n se décompose sous la forme k.l avec k et l strictement inférieurs à n. Dans ce cas, l'hypothèse de récurrence implique que les entiers k et l peuvent s'écrire comme produits de nombres premiers. Leur produit aussi, ce qui fournit une décomposition en produit de nombres premiers de n.
Par application du principe de récurrence, tous les entiers naturels peuvent s'écrire comme produit de nombres premiers.
Des variantes de cette démonstration s'appuyant sur le principe de descente infinie de Fermat, ou sur l'existence d'une borne inférieure à toute partie de N sont essentiellement équivalentes.
(2) Unicité
La preuve de l'unicité peut être obtenue à partir du lemme d'Euclide selon lequel, si un nombre premier p divise un produit ab, alors il divise a ou il divise b (lemme qui découle lui-même de l'identité de Bézout)). Maintenant, prenons deux produits de nombres premiers qui sont égaux. Prenons n'importe quel nombre premier p du premier produit. Il divise le premier produit, et, de là, aussi le second. Par ce qui précède, p doit alors diviser au moins un facteur dans le second produit. Mais les facteurs sont tous des nombres premiers eux-mêmes, donc p doit être égal à un des facteurs du second produit. Nous pouvons donc simplifier par p les deux produits. En continuant de cette manière, nous voyons que les facteurs premiers des deux produits coïncident précisément.
Autre démonstration de l'unicité
Une autre démonstration de l'unicité de la factorisation d'un entier donné utilise la descente infinie.
On suppose qu'un certain entier peut être écrit comme (au moins) deux produits différents de nombres premiers, alors il doit exister un plus petit entier s avec ce genre de propriété. Appelons les deux produits égaux à s respectivement p1 × ... × pm et q1 × ... × qn. Il ne peut y avoir de facteur commun entre les deux produits, sinon il existerait un entier plus petit factorisable de deux manières (en simplifiant les facteurs premiers communs des deux produits). Nous pouvons maintenant assurer sans perte de généralité que p1 est un facteur premier plus petit que n'importe quel q j (avec 1 ≤ j ≤ n). Divisons q1 par p1 : il existe des entiers d et r tels que q1 = p1 × d + r avec 0 < r < p1 (r ne peut être nul puisque q1 est premier et p1 < q1). Par substitution dans q1 × ... × qn nous obtenons immédiatement p1 × ... × pm = p1 × d × q2 × ... × qn + r × q2 × ... × qn. On voit que p1 divise le premier membre de l'égalité ci-dessus ainsi que le premier terme du second membre. Il divise donc aussi r × q2 × ... × qn. Or comme r < p1 < q1 on voit que r × q2 × ... × qn est strictement inférieur à s et admet donc une unique factorisation en nombres premiers. Or p1 divise ce nombre donc devrait en être un facteur premier, mais ne peut être aucun des q j (2≤j) ni aucun des facteurs premiers de r puisque r < p1 d'où la contradiction. Donc, l'affirmation de départ doit être fausse, ce qui montre l'unicité de la décomposition.Applications
Le théorème fondamental de l'arithmétique implique que tout entier naturel admet un facteur premier. Euclide utilisa ce résultat pour démontrer que les nombres premiers sont en quantité inépuisable : pour une famille finie de nombres premiers, le produit des éléments de cette famille augmenté de 1 est soit premier, soit divisible par un nombre premier qui n'est pas dans la famille initiale. En conséquence, aucune famille finie ne contient tous les nombres premiers (cf Théorème d'Euclide sur les nombres premiers).
Le théorème fondamental intervient explicitement dans l'étude des fonctions additives et multiplicatives. En particulier, toute fonction complètement multiplicative est uniquement déterminée par les valeurs prises en les entiers premiers.
Toutefois, la preuve de l'existence donnée ci-dessus ne donne pas un algorithme efficace de la recherche de la décomposition d'un entier naturel en produit de nombres premiers.
Notes et références
- ↑ Lire la proposition 31 du livre VII
Voir aussi
Portail des mathématiques
Catégories : Divisibilité et factorisation | Arithmétique modulaire | Théorème de mathématiques
Wikimedia Foundation. 2010.
