Localisation (mathematique)

Pour les articles homonymes, voir Localisation.

Notion intuitive

La localisation est une des opérations de base sur un anneau commutatif unitaire. Il s'agit d'une construction plus générale que celle du corps des fractions. Elle consiste à plonger l'anneau dans un anneau plus grand dans lequel on a autorisé des divisions que l'on ne faisait pas avant. Par exemple, le localisé de 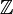en 7 est l'anneau , dans lequel tout nombre entier qui n'est pas multiple de 7 admet un inverse. Cet anneau correspond à une structure d'anneau à valuation discrète car il est de plus principal.

Définition rigoureuse

On définit une partie multiplicative S d'un anneau A comme étant une partie de A contenant 1, et stable par multiplication.

La localisation de l'anneau A en la partie S est alors un anneau, noté S ^{− 1}A, et un morphisme 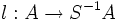, tels que: 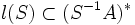, et qui soient universels pour cette propriété; c'est-à-dire que pour tout morphisme d'anneaux 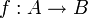, si 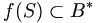, alors il existe un unique morphisme 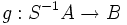tel que .

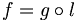Construction

Pour construire l'anneau localisé, on procède comme dans la construction du corps des fractions mais avec une précaution supplémentaire pour tenir compte du fait que l'anneau n'est pas toujours intègre. Sur le produit cartésien 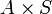, la relation d'équivalence est alors la suivante : (a,s)˜(a',s') si et seulement s'il existe un élément 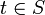tel que t(as' − a's) = 0. Le reste de la construction est la même que celle du corps des fractions (le lecteur s'y réferera). L'utilisation de l'élément t est cruciale pour la transitivité.

Exemples importants

• Les éléments réguliers 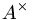forment une partie multiplicative; l'anneau 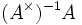est l'anneau total des fractions de A;
• Le complémentaire d'un idéal premier p est une partie multiplicative, et peut donc servir pour localiser l'anneau. Dans ce cas, on note A_p = (A − p) ^{− 1}A. C'est un anneau local appelé localisé de A en p.
• Lorsque A est un anneau intègre, le premier exemple est un cas particulier du second. En effet, l'idéal nul est premier et son complémentaire est 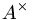. Dans ce cas, 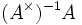est un corps appelé corps des fractions de A. L'application canonique qui va de l'anneau dans son corps des fractions est injective.
• Lorsque A n'est pas un anneau intègre, le complémentaire d'un idéal premier peut contenir des diviseurs de zéros. Vu que l'image dans l'anneau des fractions d'un diviseurs de zéro a est inversible, cela entraine que l'image de tous les b tels que ab = 0 est nulle. L'application de l'anneau dans l'anneau des fractions n'est alors pas injective. Par exemple, considérons l'anneau produit K² lorsque K est un corps. Il possède deux idéaux maximaux 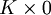et . 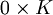Les deux corps de fractions sont alors isomorphes à K et les deux applications canoniques sont en fait les deux projections. Dans ce cas, on constate que vouloir inverser des éléments n'augmente pas le nombre de ceux-ci mais au contraire le diminue.
• Soit f un élément de A. L'ensemble S union de {1} et des puissances fⁿ positives forment une partie multiplicative de A. La localisation de A par rapport à cette partie multiplicative est notée A_f. Notons que A_f est l'anneau nul si et seulement si f est nilpotent. Lorsque A est intègre, A_f est l'ensemble des fractions qui peuvent s'exprimer comme le quotient d'un élément de A par une puissance positive de f.

Exemple explicatif

• Si l'on prend l'anneau des polynômes, . Son spectre d'anneau s'apparente alors au plan complexe. Le localisé en l'idéal premier 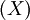s'appelle le localisé en 0 et est précisément l'anneau des polynômes dans lequel on a autorisé toutes les divisions exceptées celles par un multiple de X. Ce nouvel anneau permet de s'intéresser aux propriétés des polynômes au voisinage de 0, d'où le terme de localisé.

Spectre d'une localisation

Soit S une partie multiplicative de A. Alors l'ensemble des idéaux premiers de S ^{− 1}A peut s'identifier à la partie des idéaux premiers de A disjoints de S. Plus précisément, soit 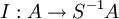le morphisme canonique. Pour tout idéal premier Q de S ^{− 1}A, I ^{− 1}(Q) est un idéal premier de A qui est disjoint de S, et cette correspondance est biunivoque, la correspondance réciproque associant un idéal premier P de A l'idéal I(P)S ^{− 1}A de S ^{− 1}A. De plus, le morphisme canonique entre les idéaux premiers 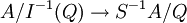induit un isomorphisme entre leurs corps des fractions.

Noter qu'en général, cette correspondance n'existe pas pour les idéaux maximaux (considérer l'exemple avec A égal à l'anneau des entiers et S ^{− 1}A son corps des fractions).

A voir

• la construction des nombres rationnels

• Portail des mathématiques