Groupe Abélien De Type Fini

Groupe Abélien De Type Fini

Groupe abélien de type fini

Les groupes abéliens de type fini forment une sous-catégorie particulière d'objets mathématiques de la catégorie des groupes abstraits. Ce sont les groupes qui sont, d'une part, abéliens, c’est-à-dire ceux dont la loi de composition interne est commutative, mais aussi sont de type fini, c’est-à-dire qu'ils sont engendrés par un nombre fini de leurs éléments.

À ce titre, cette notion relève de l'algèbre générale. Toutefois, la notion de groupe abélien, et plus particulièrement ceux qui sont de type fini, est au fondement de la notion de module: La donnée d'un groupe abélien équivaut à celle d'un module sur l'anneau universel qu'est l'anneau Z des entiers relatifs. Les groupes abéliens de type fini participent de ce fait au fondement de l'algèbre commutative.

Un intérêt majeur de l'étude de cette notion est que le fait d'imposer à un groupe d'être abélien et de type fini permet de lui appliquer le théorème de structure des groupes abéliens de type fini: On sait donner de façon élémentaire la liste de tous les types (plus précisément les classes d'isomorphisme) de groupes abéliens de type fini que l'on peut rencontrer. Un résultat analogue pour les groupes abstraits plus généraux, même si on les suppose de type fini, voire de présentation finie, ou bien encore tout simplement fini (voir toutefois «groupe sporadique» à ce sujet), est largement hors de portée. En outre cette liste est très simple au sens où elle ne fait intervenir que les exemples de groupes les plus familiers que l'on rencontre en pratique.

Ainsi ce théorème de structure permet, pour tout objet mathématique satisfaisant les axiomes caractérisant les groupes abéliens de type fini, de se ramener une famille familière d'objets dont on connait la plupart des propriétés. Cela en fait un outil d'étude et de démonstration très efficace. En outre comme les groupes abéliens de type fini sont des objets très familiers, ils ont la propriété d'apparaitre dans de nombreuses branches et questions d'ordre mathématique, qui sont d'autant plus d'applications.

Dans un autre ordre d'idées, la notion de groupe abélien permet de manipuler des constructions comme le produit tensoriel la somme directe (et le produit), le Hom interne, et ces constructions conservent la propriété de finitude satisfaite par les groupes abéliens de type fini. Plus formellement, on obtient ainsi une catégorie stable par des opérations standard. Cela fournit un cadre commode à l'algèbre homologique, et la formation des groupes Tor et Ext.

On retrouve la notion de groupe abélien de type fini dans quelques théorèmes et thèmes centraux en mathématiques, comme le théorème des unités de Dirichlet, le théorème de Mordell-Weil et la conjecture de Mordell, via la conjecture de Mordell-Lang, en géométrie arithmétique, l'homologie simpliciale des CW-complexes de type fini et le groupe de Néron-Severi en topologie algébrique, certains groupes de classes (K-groupes) comme celui des classes d'idéaux d'un corps de nombres, des classes de représentations sur C des groupes finis, ou le groupe des caractères d'un tore algébrique.

Sommaire

Définitions et exemples

Définitions

Les groupes abéliens de type fini peuvent aussi être munis d'une structure de module. En conséquence, en plus du vocabulaire classique des groupes, se greffe un vocabulaire spécifique à la théorie des modules:

  • Dans un groupe, chaque élément engendre un sous-groupe monogène. Ce dernier est soit libre (autrement dit infini), auquel cas il est isomorphe à Z, soit cyclique (c'est-à-dire fini), et dans ce cas isomorphe au groupe Z/nZ (et ce pour un unique entier naturel non nul n). Dans le premier cas on dit que l'élément générateur est libre, ou d' ordre infini. Dans le second cas, on dit que c'est un élément de torsion, ou d' ordre fini.
  • Dans un groupe abélien, les éléments de torsion forment un sous-groupe, le sous-groupe de torsion. Si tout élément est de torsion, c'est-à-dire si le sous-groupe de torsion est le groupe abélien tout entier, on dit alors que ce groupe abélien lui-même est un groupe de torsion.

A contrario un groupe non abélien peut être engendré par des éléments de torsion sans que tous ses éléments soient de torsion. Le groupe PSL(2,Z), par exemple, admet une partie génératrice formée d'un élément d'ordre 2 et un élément d'ordre 3, et contient pourtant des éléments d'ordre infini. Le sous-ensemble formé des éléments d'ordre infini ne définit, quant à lui, jamais un sous-groupe : l'élément neutre est toujours d'ordre 1, donc de torsion.

  • Un groupe abélien est dit groupe abélien libre s'il admet une base. Dans le cas des groupes abéliens de type fini, cela n'est le cas que si le groupe de torsion se réduit à l'élément neutre.

Le groupe additif Q des nombres rationnels a, quant à lui, un sous-groupe de torsion réduit à son élément neutre, le zéro. Il n'admet pourtant aucune base: En effet deux quelconques de ses éléments sont toujours liés, et le groupe Q n'est ni réduit à zéro (cas d'une base vide), ni monogène (ce qui serait le cas s'il avait une base réduite à un seul élément).

  • Pour chaque nombre premier p, un élément de torsion d'un groupe abélien est dit de p-torsion si son ordre est une puissance de p. Seul l'élément neutre est de p-torsions pour différents nombres premiers p.
  • Le lemme chinois permet de montrer que, dans un groupe abélien, tout élément de torsion se décompose, de manière unique, en somme d'un seul élément de p-torsion pour chaque nombre premier p divisant l'ordre de cet élément de torsion. Le terme associé à chacun de ces nombres premiers s'appelle la p-composante de cet élément.

Cette décomposition peut s'interpréter comme la décomposition du sous-groupe de torsion comme produit de p-groupes. Le théorème de structure des groupes abéliens de type fini (voir ci-dessous) est un résultat analogue qui prend en compte les éléments d'ordre infini.

Exemples

  • Z le groupe des entiers est un groupe abélien libre monogène.
  • Z l ou l est un entier est un groupe abélien libre de type fini.
  • Z/a Z est un groupe de torsion monogène.
  • Z/a1 Z x Z/a2 Z x ... x Z/ak Z est un groupe de torsion de type fini.
  • Z l x Z/a1 Z x Z/a2 Z x ... x Z/ak Z est un groupe abélien de type fini.

On remarque que les quatre premiers exemples correspondent à des cas particuliers du cinquième. Les groupes abéliens de type fini sont parfaitement compris en cela qu'ils sont tous isomorphes à une structure de type celui du cinquième exemple.

Relation avec les modules

Soit g un élément de G et n un entier positif. L'expression n.g possède un sens. En effet, elle désigne l'élément de G obtenu par l'addition n fois de g. De même l'expression -n.g signifie l'inverse de n.g ou n fois l'addition de l'opposé de g.

Ces remarques permettent de conclure que Z opère sur le groupe. Il est aisé de vérifier que les axiomes définissant la structure de module sont vérifiés. En conclusion tout groupe abélien de type fini dispose d'une structure naturelle de Z module.

Cette notion permet d'identifier un groupe abélien de type fini avec un Z module. La théorie devient alors analogue à celle des espaces vectoriels. Il est possible de parler de famille génératrice, de famille libre et donc de base. En revanche, le théorème du rang ne s'applique pas. En effet, sur Z/6 Z, la classe de 1 est une génératrice et aucune sous-famille ne l'est, il en est de même de la famille constituée des classes de 2 et 3. Il existe donc deux familles génératrices minimales n'ayant pas le même cardinal.

Un morphisme de groupe est aussi un morphisme de module.

Cas des groupes finis

Article détaillé : Théorème de Kronecker.

Si G est d'ordre fini, il dispose alors d'une décomposition particulièrement simple:

  • Il existe une suite d'entiers strictement positifs (a1,a2,...,ak) tel que G est isomorphe au produit direct des groupes cycliques de cardinal les différents éléments de la suite. De plus il est possible de choisir la suite tel que ai+1 divise ai si i est un entier entre 1 et k - 1.

Il existe donc la suite suivante isomorphe au groupe G:

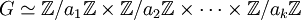
G\simeq \mathbb{Z}/a_1\mathbb{Z}\times \mathbb{Z}/a_2\mathbb{Z} \times \cdots \times \mathbb{Z}/a_k\mathbb{Z}

Ce théorème est connu sous le nom de théorème de Kronecker, la démonstration est donnée dans l'article détaillé.

Cas général

Module libre

Un groupe abélien fini considéré comme un Z module ne peut contenir de base. En effet, toute combinaison linéaire de coefficient l'exposant du groupe pour chaque élément d'une famille du groupe est égale à l'élément neutre. Il en va différemment pour les groupes libres.

  • Un groupe abélien de type fini est libre si et seulement s'il existe une base du groupe considéré comme un Z module.

On remarque alors que la donnée d'une base fournit directement un isomorphisme entre le groupe et une puissance de Z.

Dans le cas d'un groupe libre de type fini, alors le théorème définissant la dimension, analogue à celui de l'algèbre linéaire s'applique encore:

  • Les bases d'un groupe abélien de type fini libre ont toutes le même cardinal.

Ce qui implique que si n est un entier différent d'un autre entier m, alors il n'existe aucun isomorphisme entre Z n et Z m. La situation, dans le cas des groupes libres est alors analogue à celle des espaces vectoriels.

La théorie des matrices donne alors une condition nécessaire et suffisante pour qu'une famille soit une base :

  • Soit B une base d'un groupe G libre de type fini. Une famille F est une base si et seulement si la matrice de passage de B dans F possède un déterminant égal à 1 ou -1.

Certaines autres propriétés analogues aux espaces vectoriels s'appliquent encore:

  • Tout sous-groupe d'un groupe abélien libre de type fini est un sous-groupe abélien libre de type fini.
  • Tout produit direct fini de groupes abéliens libres de type fini est un groupe abélien libre de type fini.


Démonstrations

Les démonstrations proposées ici se fondent essentiellement sur la structure de Z module du groupe.

  • Si G, un groupe libre de type fini, possède une base alors son cardinal est fini et toute base de G possède le même cardinal.

Soit (ei) une base de G et (gj) une famille génératrice finie. Chaque élément gj est engendré par une partie finie de la base, et la famille génératrice finie est engendré par une partie finie de la base. Ceci démontre que la base est de cardinal fini.

Considérons alors l'application canonique ψ de G dans G/2G, l'ensemble d'arrivée peut être muni d'une structure de F2 espace vectoriel où F2 désigne le corps à deux éléments.

Montrons que (ψ(ei)) est une base de G/2G. La famille est génératrice car (ei) est une base et ψ est un morphisme de groupe surjectif.

Montrons alors que la famille est libre. Soit β1.ψ(e1) + ...+ βk.ψ(ek) une combinaison linéaire nulle de la famille (ψ(ei)) et α1.e1 + ...+ αk.ek un antécédent par ψ de cette combinaison linéaire. Comme l'antécédent est élément de 2G, chaque αi est paire, ce qui démontre que chaque βi est nul. La famille est bien libre.

En conclusion, à toute base de G est associé une base d'un F2 espace vectoriel. Or toute base d'un même espace vectoriel possède le même cardinal. Toute base de G possède donc bien le même cardinal.

  • Soit B une base de G, B' est une base de G un groupe libre de type fini, si et seulement si l'endomorphisme qui a pour image de la base B, B' est un isomorphisme. Ou encore B' est une base si et seulement si la matrice de transfert de la base B vers la base B' possède un déterminant égal à 1 ou à -1.

Si φ est un isomorphisme, alors la base B' engendre par combinaison linéaire la base B et donc le groupe G tout entier. L'unique combinaison linéaire nulle de la base B est la combinaison linéaire à coefficients nuls. L'application de l'isomorphisme φ montre que l'unique combinaison linéaire nulle de B' est aussi la combinaison linéaire à coefficients nuls.

Réciproquement si B' est une base de G, alors l'application qui associe B à B' est surjectif car B' engendre G et possède pour noyau {0} car l'unique combinaison linéaire de B' nulle est la combinaison linéaire à coefficients nuls.

Si la matrice M de transfert de B dans B' possède un déterminant inversible, alors si cM désigne la comatrice de M, l'égalité cM.M = det(M) montre le caractère inversible de l'endomorphisme de passage de la base B à la base B '. Réciproquement si l'endomorphisme de transfert de B dans B' est inversible, alors la matrice M-1 vérifie: det(M).det(M-1) = 1 ce qui montre que det(M) est inversible. La conclusion provient du fait qu'il n'existe que deux éléments inversibles dans Z: 1 et -1.

  • Soit n un entier strictement positif et (λ1, λ2, ..., λn) les coordonnées d'un élément e1 de G dans une base B. Alors e1 peut être complété en une base (e1, e2, ..., en) si et seulement si la famille des (λ1, λ2, ..., λn) ne contient que des éléments premiers dans leur ensemble.

Démontrons dans un premier temps, que la condition est nécessaire:

Si (λ1, λ2, ..., λn) n'est pas une famille de nombres premiers entre eux dans leur ensemble, alors il existe un entier l strictement supérieur à 1 et un élément z de Z n tel que e1 = l. z. Soit (e1, e2, ..., en) une famille génératrice de G. Alors l. z possède au moins deux combinaisons linaires distinctes : d'une part l fois la combinaison linéaire de z et d'autre part e1. La famille ne peut donc être une base de G.

Démontrons alors la réciproque par une récurrence sur n:

Si n est égal à 2: alors l' identité de Bézout montre l'existence de deux entiers p et q tel que : λ1.p + λ2.q = 1. Soit e2 l'élément de coordonnées (-p,q). L'endomorphisme qui à la base B associe la famille (e1, e2) possède un déterminant égal à 1. La proposition précédente permet de conclure.

Supposons le résultat vrai pour tout groupe ayant une base à p - 1 éléments. Considérons un groupe abélien de type fini ayant une base à p élément. Soit B une base et G' le groupe engendré par la famille B' des p-1 premiers éléments de B. B' est clairement une base de G'. Soit (λ1, λ2, ..., λn) une famille d'entiers premiers entre eux dans leur ensemble et soit a le pgcd de la famille (λ1, λ2, ..., λn-1). On définit μi par l'égalité a.μi = λi où i est un entier compris entre 1 et p - 1.

L'hypothèse de récurrence montre qu'il existe une famille de coefficients (cij) tel que le déterminant suivant est égal à une unité de Z que l'on peut choisir comme valant 1:

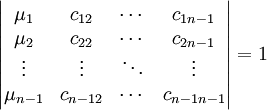
\begin{vmatrix} \mu_1 & c_{12} & \cdots & c_{1 n-1}\\ \mu_2 & c_{22} & \cdots & c_{2 n-1} \\ \vdots & \vdots &\ddots &\vdots \\ \mu_{n-1} & c_{n-1 2} & \cdots & c_{n-1 n-1} \end{vmatrix}= 1

les deux entiers a et λn sont premier entre eux, il existe donc deux entiers p et q tel que la somme p.a + q.λn soit égale à 1. Cette égalité montre que le déterminant suivant est égal à 1.

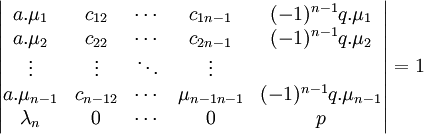
\begin{vmatrix} a.\mu_1 & c_{12} & \cdots & c_{1 n-1} & (-1)^{n-1}q.\mu_1 \\ a.\mu_2 & c_{22} & \cdots & c_{2 n-1} & (-1)^{n-1}q.\mu_2\\ \vdots & \vdots &\ddots &\vdots \\ a.\mu_{n-1} & c_{n-1 2} & \cdots & \mu_{n-1 n-1} & (-1)^{n-1}q.\mu_{n-1} \\ \lambda_n & 0 & \cdots & 0 & p \end{vmatrix}=1

La première colonne correspond aux coefficients de la famille (λ1, λ2, ..., λn). On en conclut que le déterminant correspond à une matrice de passage d'un endomorphisme inversible sur la structure de Z module, e1 est donc bien le premier vecteur d'une base de G.

Nous disposons maintenant d'une méthode puissante pour construire des bases de groupes libres de type fini, à la condition qu'au moins une base existe. C'est le cas sur Z n, mais c'est aussi le cas pour tout quotient libre de Z n.

  • Soit n un entier strictement positif et K un sous-groupe de Z n tel que le quotient Z n/K soit sans torsion. Alors il existe un entier positif m tel que Z n/K est isomorphe à Z m.

Démontrons ce résultat par récurrence sur n:

Si n est égal à 1, le seul quotient qui soit un groupe libre est obtenu avec le sous-groupe {0}. La proposition est donc vérifiée.

Supposons la proposition vrai à l'ordre p - 1. Soit K un sous-groupe de Z p tel que le quotient soit libre. Si K est réduit à l'élément neutre, alors la proposition est évidente. Dans le cas contraire, soit f un élément de K non nul. Soit a le pgcd des coefficients de f et soit f = a.ep, le morphisme canonique φ vérifie φ(f)=a.φ(ep) qui est égal à 0. La classe de ep n'est pas un élément de torsion et a.φ(ep) est égal à 0 donc ep est élément du noyau de φ.

L'élément ep est élément d'une base de Z p d'après la proposition précédente. Soit (e1, e2, ...,ep) une telle base. L'image de φ est égale à l'image du groupe G' engendré par les p -1 premiers vecteurs de la base. G' possède une base de cardinal p - 1 donc est isomorphe à Z p-1. Donc l'image de φ est isomorphe à un quotient de Z p-1 par un groupe tel que le quotient est un groupe libre. L'hypothèse de récurrence permet alors de conclure.

  • Pour groupe libre de type fini G il existe un entier n tel que le groupe soit isomorphe à Z n.

Soit une famille génératrice (e1, e2, ...,em) de G. Considérons le morphisme φ de Z m dans G définit par:

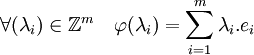
\forall (\lambda_i)\in \mathbb{Z}^m \quad \varphi(\lambda_i)=\sum_{i=1}^m \lambda_i.e_i

Le morphisme φ est par construction surjectif. Le théorème fondamental des morphismes montre alors que G est isomorphe au quotient de Z m par le noyau de φ. Ce quotient est un groupe libre, la proposition précédente montre qu'il existe n tel que ce quotient et donc G est isomorphe à Z n.

  • Tout groupe libre de type fini G admet au moins une base et toutes ses bases contiennent le même nombre d'éléments.

Il existe n un entier strictement positif tel que G soit isomorphe à Z n. Z n admet une base de cardinal fini donc G admet une base de cardinal fini. Or il a été démontré que s'il existe une base dans un groupe libre de type fini toutes les bases possèdent le même cardinal, ce qui termine la démonstration.

  • Tout sous-groupe d'un groupe abélien libre de type fini est un sous-groupe abélien libre de type fini.

Le caractère abélien et libre d'un sous-groupe est évident. Pour montrer qu'un sous-groupe d'un groupe abélien libre de type fini est de type fini, raisonnons par contraposé. Soit G un groupe abélien libre et H un sous-groupe qui n'est pas de type fini. Montrons par récurrence que, pour tout entier positif n, il existe une famille libre de ce cardinal. Si n est égal à 1, il suffit de considérer un élément non nul. Si la propriété est vraie à l'ordre p, il existe une famille libre d'ordre p et qui n'est pas génératrice car H n'est pas de type fini. Il est donc possible d'adjoindre un élément à cette famille non engendré par elle. L'adjonction de cet élément à la famille fournit une famille libre d'ordre p + 1. Le groupe G contient donc une famille libre de cardinal quelconque, il ne contient donc pas de base de cardinal fini et G n'est pas de type fini, ce qui termine la démonstration.

  • Tout produit direct fini de groupes abéliens libres de type fini est un groupe abélien libre de type fini.

Il suffit de considérer la famille union de l'image d'une base de chaque facteur du produit par les plongements canoniques.

Théorème général

La configuration générale est, là encore, relativement simple. Elle correspond à une adjonction directe des deux cas précédents. Un groupe abélien de type fini est somme directe de son sous-groupe de torsion et un sous-groupe supplémentaire libre.

  • G est la somme directe d'un sous-groupe libre Ll et d'une famille finie de sous-groupes cycliques Ci où i est un entier compris entre 1 et k. Le cardinal de Ci divise celui de Ci+1 si i est un entier compris entre 1 et k - 1.

G s'écrit donc de la manière suivante :

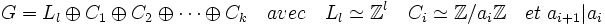
G=L_l\oplus C_1\oplus C_2 \oplus \cdots \oplus C_k \quad avec \quad L_l \simeq \mathbb{Z}^l \quad C_i \simeq \mathbb{Z}/a_i\mathbb{Z} \quad et \; a_{i+1} | a_i

Dans le cas où il existe des éléments de torsion, alors il n'existe plus de base. En effet, toute combinaison linéaire d'un élément de torsion non nul, multiplié par l'ordre de la torsion fournit une combinaison linéaire de valeur nulle à coefficients non tous nuls.

Une conséquence directe du théorème est la stabilité des groupes abéliens de type fini par produit direct fini:

  • Le produit direct fini de groupes abéliens de type fini est un groupe abélien de type fini.

Le passage au quotient conserve le caractère abélien et de type fini, en effet le morphisme canonique démontre le caractère abélien du groupe quotient car il est surjectif et l'image par ce morphisme d'une famille génératrice est génératrice:

  • Le quotient d'un groupe abélien de type fini est abélien de type fini.

Le raisonnement développé pour les sous-groupes de groupes abéliens libres de type fini s'applique sans modification, en conséquence :

  • Tout sous-groupe d'un groupe abélien de type fini est abélien de type fini.


Démonstration

Si le groupe de torsion de G est réduit à l'élément neutre, alors G est un groupe libre de type fini et le paragraphe précédent permet de conclure. Dans le cas contraire, si g1 est un élément de torsion ayant pour ordre l'exposant du groupe de torsion, alors les démonstrations du cas des groupes abéliens finis montrent qu'il existe une somme directe de G en un groupe cyclique engendré par g1 et un complémentaire H.

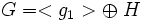
G=<g_1>\oplus\; H\;

Une récurrence analogue à celle du cas fini montre qu'il est possible d'appliquer le même raisonnement sur H jusqu'à ce que le supplémentaire ne contienne plus d'élément de torsion. G est donc somme directe d'un groupe de torsion et d'un groupe de type fini libre. L'analyse des deux situations permet alors de conclure.

Voir aussi

Liens externes

Références

S. Lang Algebre Dunod 2004
J.F. Labarre La theorie des groupes Presses Universitaires de France (PUF) 1978
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Groupe ab%C3%A9lien de type fini ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Groupe Abélien De Type Fini de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Groupe abelien de type fini — Groupe abélien de type fini Les groupes abéliens de type fini forment une sous catégorie particulière d objets mathématiques de la catégorie des groupes abstraits. Ce sont les groupes qui sont, d une part, abéliens, c’est à dire ceux dont la loi… …   Wikipédia en Français

  • Groupe abélien de type fini — En mathématiques, un groupe abélien de type fini est un groupe abélien qui possède une partie génératrice finie. Les produits, les quotients, mais aussi les sous groupes des groupes abéliens de type fini sont eux mêmes de type fini. Un théorème… …   Wikipédia en Français

  • Groupe abélien — Un groupe abélien (du nom de Niels Abel), ou groupe commutatif, est un groupe dont la loi interne est commutative. Vu autrement, un groupe commutatif peut aussi être défini comme un module sur l anneau commutatif des entiers relatifs ; l… …   Wikipédia en Français

  • Groupe de type fini — Partie génératrice d un groupe En théorie des groupes, une partie génératrice d un groupe G est une partie A telle que tout élément du groupe s écrit comme produit d un nombre fini d éléments de A et de leurs inverses. L ensemble G lui même est… …   Wikipédia en Français

  • Groupe abélien libre — En mathématiques, un groupe abélien libre est un groupe abélien qui possède une base, c est à dire une partie B telle que tout élément du groupe s écrive de façon unique comme combinaison linéaire à coefficients entiers d un nombre fini d… …   Wikipédia en Français

  • Théorème de structure des groupes abéliens de type fini — Le théorème de structure des groupes abéliens de type fini fournit une classification très explicite des groupes abéliens de type fini à isomorphisme près. Entre autres informations, il indique que tout groupe abélien de type fini est un produit… …   Wikipédia en Français

  • Groupe Abélien Fini — Leopold Kronecker (1823 1891) En mathématiques et plus précisément en algèbre, les groupes abéliens finis correspondent à une sous catégorie de la catégorie des groupes. Un groupe abélien fini est un groupe commutatif dont le cardinal est fini.… …   Wikipédia en Français

  • Groupe abelien fini — Groupe abélien fini Leopold Kronecker (1823 1891) En mathématiques et plus précisément en algèbre, les groupes abéliens finis correspondent à une sous catégorie de la catégorie des groupes. Un groupe abélien fini est un groupe commutatif dont le… …   Wikipédia en Français

  • Groupe Abélien — En algèbre générale, un groupe abélien, ou groupe commutatif, est un groupe dont la loi de composition interne est commutative, c’est à dire que pour tous les éléments , on a . Les groupes abéliens portent le nom de Niels Henrik Abel …   Wikipédia en Français

  • Groupe abelien — Groupe abélien En algèbre générale, un groupe abélien, ou groupe commutatif, est un groupe dont la loi de composition interne est commutative, c’est à dire que pour tous les éléments , on a . Les groupes abéliens portent le nom de Niels Henrik… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”