Theoreme de Kronecker-Weber

Theoreme de Kronecker-Weber

Théorème de Kronecker-Weber

Le théorème de Kronecker-Weber établit en théorie algébrique des nombres le résultat suivant : chaque extension abélienne finie du corps des nombres rationnels \mathbb{Q}, ou en d'autres mots chaque corps de nombres algébriques avec un groupe de Galois abélien absolu, est un sous-corps d'une extension cyclotomique, i.e. un corps obtenu en adjoignant une racine de l'unité aux nombres rationnels.

Ce théorème a été énoncé par Kronecker en 1853. Sa proposition de preuve était incomplète. Weber en 1886 proposa une nouvelle preuve, qui présentait encore une lacune. Hilbert le montra en 1896 en utilisant des méthodes différentes de celles de ses prédécesseurs. Le théorème est aujourd'hui habituellement démontré comme une conséquence de la théorie des corps de classes. Cependant, il peut aussi être déduit de l'assertion analogue sur les corps de nombres p-adiques : si p est un nombre premier, et K/Qp est une extension abélienne finie, alors K est inclus dans une extension cyclotomique de Qp.


Déduction du théorème global depuis le théorème local

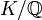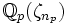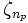Pour déduire le théorème global du théorème local, on considère pour chaque nombre premier p ramifié dans l'extension K/\mathbb{Q}, un entier np tel que K soit inclus dans \mathbb{Q}_p(\zeta_{n_p}), où \zeta_{n_p} est une racine primitive npème de l'unité. Considérant alors, pep la plus grande puissance de p divisant np, on montre alors que K est inclus dans 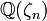\mathbb{Q}(\zeta_n), pour n le produit des pep, et ζn une racine primitive nème de l'unité. En effet, l'extension 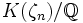K(\zeta_n)/\mathbb{Q} n'est ramifiée qu'en les nombres premiers ramifiés dans K, et n'admet aucune sous-extension partout non ramifiée (ce résultat est classiquement démontré comme conséquence d'une estimation du discriminant par le théorème de Minkowski en géométrie des nombres), donc son groupe de Galois est engendré par ses sous-groupes d'inertie en les nombres premiers p. Le cardinal de ce groupe est donc majoré par le produit des cardinaux des groupes d'inrtie locaux correspondants, qu'on trouve être égal au degré de l'extension 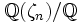\mathbb{Q}(\zeta_n)/\mathbb{Q}, ce qui conclut la démonstration.

La démonstration du cas local du théorème demande de bien connaître les propriétés de ramification des extensions cyclotomiques locales, puis de se ramener au cas d'extensions cycliques d'ordre une puissance d'un nombre premier q, et de discuter suivant que q=p ou non, le cas p=2 devant être traité encore à part.

Pour une extension abélienne donnée K de Q, il existe en fait un corps cyclotomique minimal qui la contient. Le théorème permet de définir le conducteur f de K, comme le plus petit nombre entier n tel que K soit inclus dans le corps engendré par les racines n-ièmes de l'unité. Par exemple, les corps quadratiques ont comme conducteur la valeur absolue de leurs discriminants, un fait généralisé en théorie des corps de classes.

Références


  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de Kronecker-Weber ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de Kronecker-Weber de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Théorème de kronecker-weber — Le théorème de Kronecker Weber établit en théorie algébrique des nombres le résultat suivant : chaque extension abélienne finie du corps des nombres rationnels , ou en d autres mots chaque corps de nombres algébriques avec un groupe de… …   Wikipédia en Français

  • Théorème de Kronecker-Weber — Le théorème de Kronecker Weber établit en théorie algébrique des nombres le résultat suivant : toute extension abélienne finie du corps des nombres rationnels, c est à dire tout corps de nombres algébriques dont le groupe de Galois sur est… …   Wikipédia en Français

  • Theoreme de Hilbert-Speiser — Théorème de Hilbert Speiser En mathématiques, le théorème de Hilbert Speiser est un résultat sur les corps cyclotomiques, caractérisant ceux avec une base intégrale normale. Plus généralement, il s applique à toute extension abélienne K du corps… …   Wikipédia en Français

  • Théorème de hilbert-speiser — En mathématiques, le théorème de Hilbert Speiser est un résultat sur les corps cyclotomiques, caractérisant ceux avec une base intégrale normale. Plus généralement, il s applique à toute extension abélienne K du corps des nombres rationnels . Le… …   Wikipédia en Français

  • Kronecker — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Kronecker peut désigner Leopold Kronecker (1823 1891), un mathématicien et logicien allemand, et dont les articles suivants portent le nom :… …   Wikipédia en Français

  • Kronecker Jugendtraum — Le théorème de Kronecker Weber, d abord annoncé par Kronecker, dont la démonstration fut complétée par Weber et Hilbert, décrit les extensions abéliennes du corps des rationnels. Celles ci sont contenues dans les extensions cyclotomiques, c est à …   Wikipédia en Français

  • Théorème de Hilbert-Speiser — En mathématiques, le théorème de Hilbert Speiser (de) est un résultat sur les sous corps des corps cyclotomiques, caractérisant ceux qui possèdent une base normale d entiers. D après le théorème de Kronecker Weber, les extensions abéliennes… …   Wikipédia en Français

  • WEBER (H. M.) — WEBER HEINRICH MARTIN (1842 1913) Universalité. C’est le mot qui caractérise peut être le mieux le mathématicien allemand Heinrich Weber. Esprit souple, il était capable de travailler dans des domaines très divers des mathématiques. Mais il… …   Encyclopédie Universelle

  • Leopold Kronecker — Pour les articles homonymes, voir Kronecker. Leopold Kronecker Leopold Kronecker Naissance 7 décembre 1823 Legn …   Wikipédia en Français

  • KRONECKER (L.) — Le mathématicien allemand Kronecker nous apparaît, avec Kummer, comme l’un des plus grands arithméticiens du XIXe siècle et l’un des fondateurs de la «grande» théorie des nombres algébriques. Ses travaux sur le corps de classes dans un cas… …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”