Polynome minimal d'un nombre algebrique

Carl Friedrich Gauß utilise des polynômes minimaux appelés cyclotomiques pour déterminer les polygones constructibles à la règle et au compas.

En mathématiques, le polynôme minimal d'un nombre algébrique est une notion dérivée de l'algèbre linéaire, elle est à la base de deux théories.

La théorie classique de Galois a pour champs d'étude certains corps commutatifs, construits par des extensions finies de corps initiaux comme un corps fini ou celui des nombres rationnels. Le polynôme minimal fournit une méthode naturelle pour construire de tels extensions. Ces racines sont utilisées pour élucider les propriétés d'une notion fondatrice, le groupe de Galois. Un théorème clé, comme celui de l'élément primitif s'exprime en termes de polynôme minimal.

La théorie algébrique des nombres étudie les entiers algébriques. Ils se définissent à l'aide d'un polynôme minimal. Son analyse permet d'expliciter les propriétés d'outils de l'arithmétique comme le discriminant d'un anneau, la norme d'un nombre algébrique ou la forme trace. Les propriétés d'un polynôme minimal d'un entier algébrique sont utilisées pour la démonstration de nombreux résultats, comme la structure du groupe des classes d'idéaux ou le théorème des unités de Dirichlet. Un exemple relativement simple d'utilisation est celui des corps quadratiques, cadre d'étude des nombres algébriques inclus dans une extension quadratique.

Il existe en algèbre linéaire une notion connexe, appelée polynôme minimal d'un endomorphisme.

Définition

Ici K désigne un corps et L une extension de K, c'est-à-dire un corps contenant K. Les lettres C, R et Q désignent respectivement les corps des complexes, réels et rationnels.

• Soit l un élément de L, le polynôme minimal du nombre l est, s'il existe, le polynôme unitaire de plus bas degré à coefficients dans K admettant l pour racine.

• Un élément l de L est dit algébrique sur K si et seulement s'il possède un polynôme minimal.

Le nombre π + i de l'ensemble C est algébrique si C est considéré comme une extension de R. En effet, son polynôme minimal existe et est égal à : X² -2π X + π² - 1. Ferdinand von Lindemann (1852 1839) montre^[1] que π n'est pas un nombre algébrique sur le corps des rationnels. En conséquence, π + i n'admet pas de polynôme minimal dans Q. En revanche, i l'unité imaginaire et √2 possèdent des polynômes minimaux dans Q, ils sont respectivement égaux à X² + 1 et X² - 2.

Contexte

Motivation

Évariste Galois est à l'origine d'une théorie mettant en évidence les conséquences des propriétés des polynômes minimaux.

En 1801, Carl Friedrich Gauss (1777-1855) étudie le polynôme minimal à coefficients rationnels de la racine n^ième de l'unité dans le corps des complexes^[2] et lui donne le nom de polynôme cyclotomique. Cette approche est fructueuse, l'étude de son degré ainsi que des opérations réalisables sur les racines mettent en évidence des propriétés de ces racines. Il en conclut par exemple que l'heptadécagone, c'est-à-dire le polygone régulier à 17 cotés est constructible à la règle et au compas.

Cette approche est généralisée^[3] par Évariste Galois (1811 - 1832). Il étudie systématiquement les extensions K contenant toutes les racines d'un polynôme irréductible P[X] à coefficients rationnels. Un tel polynôme est le polynôme minimal de chacune des racines. Il étudie ainsi le problème de l'extraction de racine par radical (c'est-à-dire une racine n^ième d'un rationnel) d'un polynôme irréductible.

En termes contemporains, une telle démarche permet de disposer de résultats provenant de quatre structures algébriques différentes. Le corps K peut être vu comme un espace vectoriel, si k est un élément du corps, l'application de K dans K, qui à x associe k.x est un endomorphisme de K, vu comme un Q espace vectoriel, son polynôme minimal au sens des endomorphisme correspond au polynôme minimal de l'entier algébrique k, l'algèbre linéaire est disponible avec une telle approche. Il est relativement facile de constater que tout automorphisme de K permutent les racines de P[X], ils forment donc un groupe fini isomorphe à un sous-groupe des permutations des racines. Un tel groupe porte le nom de groupe de Galois et la théorie des groupes offrent des théorèmes pour mieux comprendre une telle structure. Enfin, l'anneau des polynômes à coefficients dans Q dispose de propriétés fortes, il est par exemple euclidien. Cette richesse permet à Galois d'offrir une nouvelle formulation du théorème d'Abel, donnant une condition nécessaire et suffisante pour qu'un polynôme soit résoluble par radical.

Le polynôme minimal est à l'origine de la définition de K, il dispose de nombreuses propriétés provenant de l'algèbre linéaire, des propriétés du corps K ou encore du groupe de Galois.

Théorie algébrique des nombres

Leonhard Euler est un précurseur. Il comprend l'intérêt de nombres ayant un polynôme minimal à coefficients entiers. Une maitrise insuffisante des structures maintenant appelées anneau conduit néanmoins à glisser une erreur dans sa démonstration.

L'intérêt pour le polynôme minimal possède aussi une autre origine. La résolution de certaines équations diophantiennes comme celle des deux carrés est simplifiée si un nouvel anneau est utilisé. Gauss découvre à cette occasion^[4] les entiers portant maintenant son nom. Ils correspondent aux complexes de la forme α + i.β, où α et β sont des entiers naturels. Si p est un nombre premier congru à 1 modulo 4, alors il existe un morphisme de l'anneau des entiers de Gauss, vers Z/pZ. Le noyau de ce morphisme est un idéal principal de générateur un nombre α + i.β tel que α² + β² est égal à p, ce qui permet de résoudre l'équation.

Une démarche de cette nature possède un célèbre antécédent, Leonhard Euler (1707 - 1783) utilise les nombre de la forme α + i√3.β pour tenter de démontrer le dernier théorème de Fermat pour n = 3. Il annonce^[5] à Goldbach en 1753 qu'il a enfin trouvé une solution. Elle se révèle fausse^[6], il suppose implicitement que l'anneau considéré est euclidien. Ce n'est pourtant pas le cas, comme le montre l'égalité suivante :

Les trois nombres utilisés n'ont pas de diviseurs autre que 1 ou le nombre lui-même (à un nombre inversible près). Ferdinand Eisenstein (1823 1852) finit par trouver le bon anneau d'entiers équivalent, il est formé des nombres de la forme α + j.β où j désigne une racine cubique de l'unité.

La bonne définition d'un entier algébrique d'une extension finie de Q est celle des nombres dont les coefficients du polynôme minimal sont des entiers naturels. Cet ensemble forme un anneau. Si dans le cas général, il n'est pas euclidien, il possède néanmoins suffisamment de propriétés pour permettre de bâtir une théorie. L'anneau est dit de Dedekind. Si l'anneau n'est en général ni euclidien ni factoriel, le passage à la notion d'idéal fractionnaire montre que tout idéal est le produit, d'une manière unique d'idéaux premiers. Cette propriété est fondatrice de la théorie algébrique classique des nombres, elle remplace la décomposition en facteurs premiers perdue dans le cas général.

Le polynôme minimal est ainsi l'outil de définition d'un entier algébrique. Ses propriétés, dérivées de l'arithmétique, l'algèbre linéaire et la théorie de Galois, sont utilisées pour établir les théorèmes clé de la théorie comme celui de Dirichlet ou celui sur le groupe des classes d'idéaux.

Théorie de Galois

Propriétés élémentaires

Ici K est un corps, L une extension de K et m un élément de L.

La structure euclidienne de K[X] permet d'établir une première propriété :

• Soit P[X] un polynôme irréductible et unitaire de K[X], alors il existe une extension E de K de dimension le degré n de P[X] contenant un élément e tel que P[X] soit le polynôme minimal de E.

En effet, l'idéal engendré par P[X] est maximal car P[X] n'admet pas d'autre diviseurs que 1 et lui-même (à un facteur multiplicatif près). Le quotient de K[X] par cet idéal est un corps. Si e désigne la classe de X dans ce corps, e est racine de P[X]. La dimension de cette extension est égal au degré de P[X] car 1, e, ..., e^n-1 est une base du quotient. L'ensemble des polynômes à coefficients dans K admettant e pour racine est un idéal de K[X], il contient P[X]. Comme K[X] est principal car euclidien, l'idéal est engendré par un polynôme, de degré minimal, non constant et qui divise P[X]. Ce polynôme est nécessairement P[X] car il est irréductible.

L'algèbre linéaire permet d'établir quelques propriétés sur les polynômes minimaux. Supposons que m soit algébrique sur K, c'est-à-dire qu'il possède un polynôme minimal à coefficients dans K.

• La dimension n de la plus petite extension contenant m est égal au degré du polynôme minimal M[X].

Il suffit de remarquer que 1, m, ..., m^n-1 est une base de la plus petite extension.

• Si m est élément d'une extension finie E sur K (c'est à dire de dimension finie), alors il admet un polynôme minimal à coefficients dans K.

L'application f de E dans E qui à x associe m.x est un endomorphisme. Tout endomorphisme sur un espace vectoriel de dimension fini possède un polynôme minimal et en particulier f. Le polynôme minimal de l'endomorphisme f est par construction le polynôme minimal du nombre algébrique m.

• Si m₁ et m₂ sont deux entiers algébriques, alors m₁.m₂ et m₁ + m₂ admettent des polynômes minimaux à coefficients dans K. Si m₁ est inversible, alors m₁^-1 l'est aussi.

• Soit E une extension finie de K et si m admet un polynôme minimal à coefficients dans E, il admet aussi un polynôme minimal à coefficients dans K.

Les deux dernières propriétés sont démontrés dans l'article détaillé.

Extension séparable

Un polynôme est dit séparé s'il admet autant de racines distincts que son degré. Il est donc scindé. S'il existe toujours une extension contenant toutes les racines d'un polynôme minimal, il n'est pas nécessairement séparable. Il peut en effet posséder des racines multiples. Tel n'est pas le cas si le corps est parfait, par exemple si K est fini ou de caractéristique nulle. Les extensions séparables possèdent des propriétés supplémentaires importantes. Dans le cas général la proposition suivante est vraie :

• Soit E une extension finie de K et e un élément de E, le degré du polynôme minimal n de e à coefficients dans K divise la dimension de E.

Cette propriété est démontrée dans l'article Extension algébrique. Elle permet par exemple de démontrer que la trisection de l'angle ou la duplication du cube est en général impossible à la règle est au compas (cf l'article Tour d'extension quadratique).

Une propriété plus forte est vraie si l'extension est séparable :

• Soit E une extension séparable et finie, alors il existe un élément e dont le polynôme minimal sur K est de degré la dimension de E.

L'élément engendre l'extension. Ce résultat est connu sous le nom de théorème de l'élément primitif.

Groupe de Galois

Le groupe de Galois G est formée de l'ensemble des automorphismes de L laissant invariants K. Si σ est un élément du groupe de Galois de L et P[X] le polynôme minimal de m, alors σ(m) est aussi une racine de P[X]. En effet, les propriétés de morphisme des membres du groupe de Galois montrent que :

Les propriétés sont plus fortes si L est une extension galoisienne. Une extension galoisienne, si L est de dimension finie est une extension séparable et dont le groupe de Galois contient autant d'éléments que la dimension de L. Dans le cas général une extension galoisienne est une extension séparable tel que tout automorphisme d'une extension de L laissant invariant K laisse aussi globalement invariant L (c'est-à-dire que l'image de L par l'automorphisme est égal à L).

Supposons que L soit une extension finie galoisienne de dimension d en tant que K espace vectoriel et notons σ₁, σ₂, ..., σ_d les différents éléments de G. Alors le polynôme P[X] est scindé dans L et ne contient aucune racine multiple. De plus, pour toute racine r de P[X], il existe au moins un entier i entre 1 et d tel que σ_i(m) est égal à r. Plus précisément :

• Il existe un entier n tel que l'égalité polynomiale suivante soit vraie :

La valeur n est égal au rapport entre l'ordre du groupe G et le degré de P[X].

Démonstration

En effet, le polynôme de droite est invariant par le groupe de Galois car la composée par un élément d'un groupe est une permutation des éléments du groupe. Les seuls éléments invariants par le groupe le Galois est K (cette propriété est démontrée dans l'article détaillé). Le polynôme de droite est un polynôme à coefficients dans K et annulant m donc multiple du polynôme minimal. Soit H le sous-groupe de G laissant invariant K[m], le plus petit corps de L contenant K et m et appelé corps de rupture. Soit K l'ensemble des classes à droite du quotient de G par H. Si K n'est en général pas un sous-groupe car H n'est pas nécessairement distingué, K forme une partition de H et si k_r est le représentant d'une classe, alors la translation à gauche de k_r est une bijection de H dans la classe de k_r. Si K_r est un ensemble contenant un unique représentant pour chaque classe de K et n désigne l'ordre de H, on a :

On en déduit les égalités suivantes :

Puisque Qⁿ[X] admet m pour racine, il en est de même pour Q[X]. On remarque que la composée du polynôme Q[X] par un élément du groupe de Galois donne un produit sur un autre jeu de représentants pour chaque classe de K et donc est invariant par cet élément. Comme Q[X] est invariant par tous les éléments du groupe de Galois, c'est un polynôme de K[X]. Toutes les racines de Q[X] sont des racines de P[X], le polynôme Q[X] divise P[X], le seul polynôme unitaire ayant m pour racine et divisant P[X] est P[X], on en déduit que les deux polynômes sont confondus.

 

Outils issus de l'algèbre linéaire

Dans tout ce paragraphe, on suppose que l'extension L est finie et galoisienne.

Théorème de Cayley-Hamilton

L'algèbre linéaire offre de nombreux outils, que la remarque suivante permet d'utiliser : L est un espace vectoriel sur K, l'application φ_m de L dans L qui à x associe m.x est un endomorphisme. Son polynôme minimal en tant qu'endomorphisme est le même que celui du nombre algébrique m.

Soit P[X] le polynôme minimal de m dans K et K[m] le corps de rupture de P[X] contenant m. Le corps L est un K[m] espace vectoriel soit n sa dimension et (l₁, ... l_n) une base de L en tant que K[m] espace vectoriel. Tout vecteur l de L s'exprime comme une combinaison linéaire des éléments de la base avec des coefficients dans K[m], c'est-à-dire s'exprimant comme l'image de polynômes de degré inférieur ou égal à d le degré de P[X] :

On en déduit que la famille (mⁱ.l_j) si i varie de 0 à d - 1 et j de 1 à n forme une base de L en tant que K espace vectoriel.

Dans ces bases l'expression matricielle de φ_m et de sa restriction à K[m] est simple. Soit M_K[m] la matrice de la restriction de φ_m à K[m] dans la base (1, m, ... m^d-1), on a :

On en déduit la proposition suivante :

• Sur son corps de rupture, le polynôme minimal et le polynôme caractéristique de φ_m sont confondus.

Dans L, on obtient une expression matricielle M_L en matrices blocs analogue à la réduction de Jordan, ainsi que celle du polynôme caractéristique χ[X] :

Ce résultat fournit une preuve, dans un cas particulier du théorème de Cayley-Hamilton, ainsi que l'égalité suivante :

Ici la famille (σ₁, σ₂, ..., σ_d) décrit les éléments du groupe de Galois.

Norme

Dans ce paragraphe L est de dimension finie d en tant que K espace vectoriel, l est un élément de L et φ_l désigne l'endomorphisme du K espace vectoriel L qui à x associe l.x.

L'algèbre linéaire fournit des outils supplémentaires à la théorie de Galois et à la théorie algébrique des nombres. La norme est un exemple.

La norme relative à L dans K de l correspond au déterminant de l'endomorphisme φ_l. Elle est en général notée N_L/K(l). Avec les notations précédentes, si l'extension est galoisienne, elle vérifie :

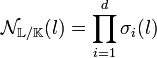
En effet, le déterminant est égal au coefficient constant du polynôme caractéristique calculé précédemment. Par définition, elle prend ses valeurs dans K.

A la différence de la norme relative, la norme est indépendante de l'extension. Elle correspond au déterminant précédent si L est le corps de rupture de l. Si D est le corps de décomposition de l et si G désigne son groupe de Galois, l'égalité suivante est vérifiée :

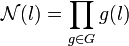
Les résultats précédents montrent que si n est la dimension de D en tant que L espace vectoriel, la norme à la puissance n est égale à la norme relative. La norme est aussi un élément de K.

Forme trace

La trace est une application un peu de même nature que la précédente. La trace de L sur K de l'élément l est égal à la trace de l'endomorphisme φ_l. La trace d'un élément l est donc égale au coefficient sous dominant du polynôme minimal. L'application qui à deux éléments a et b de L associe la trace de a.b est appelée forme trace. Elle joue un rôle important en théorie algébrique des nombres, par exemple pour définir le discriminant.

Anneau des entiers algébriques

Il est possible de définir le polynôme minimal dans un cadre plus vaste que le précédent. Soit A et B deux anneaux commutatifs unitaires et intègres, tel qu'il existe un morphisme ψ de A vers B. Souvent le morphisme est injectif et A est un sous anneau de B.

La donnée de ce morphisme permet de considérer B comme un A module. la multiplication externe d'un élément a par un élément b est donnée par a.b = ψ(a).b. On vérifie bien qu'une telle structure confère à B le statut de A module. La multiplication interne de B permet de considérer cet ensemble comme une A algèbre sur un anneau.

• Le polynôme minimal d'un élément b de B est un polynôme P[X] de A[X] unitaire tel que ψ(P[b]) est égal à zéro.

Si P[X] = a₀ + a₁X + ... + Xⁿ, alors ψ(P[b]) = ψ(a₀) + ψ(a₁)b + ... + bⁿ. On encore avec la notation associée à un A module P[b] = a₀ + a₁b + ... + bⁿ.

• Un élément de b admettant un polynôme minimal à coefficients dans A est dit entier dans A.

Un exemple important est celui où A est égal à Z et B est une extension de Q. Les entiers de Q si l'anneau A est égal à Z est l'ensemble Z lui-même. Le cas où B est égal à Q[i] est traité dans l'article Entier de Gauss, le cas où B est égal à Q[j], si j désigne une racine cubique de l'unité dans l'ensemble des complexes est traité dans l'article Entier d'Eisenstein, le cas Q[√5] dans Entier de Dirichlet. Le cas général des entiers des extensions quadratiques de Q dans corps quadratique.

Un propriété importante est le fait que si b₁ et b₂ sont deux éléments de B entiers dans A alors b₁ + b₂, b₁.b₂ et -b₁ admettent des polynômes minimaux dans A. Ainsi l'ensemble des entiers de B forme un anneau.

• Les quatre conditions suivantes sont équivalentes :

1. L'élément b admet un polynôme minimal.
2. La A-algèbre A[b] possède une famille génératrice finie.
3. Il existe une sous-algèbre C de B contenant b et possédant une famille génératrice finie.
4. Il existe un existe un sous-A module D de B stable par multiplication par b, contenant un élément qui n'est pas diviseur de zéro et possédant une famille génératrice finie.

Le terme famille génératrice est pris ici au sens de A module. Cela signifie que tout élément de la sous-algèbre est combinaison linéaire de la famille, avec des coefficients choisis dans A.

Ainsi, si b₁ et b₂ admettent chacun un polynôme minimal, il existe deux familles génératrices finies générant chacune une sous-algèbre contenant l'une b₁ et l'autre b₂. La famille composée des produits d'un élément de chaque famille est une sous algèbre admettant une famille génératrice finie et contenant b₁ + b₂, b₁.b₂ et -b₁, ce qui montre que ces éléments sont des entiers sur A et permet d'énoncer la propriété suivante :^[7]

• L'ensemble des éléments de B entiers sur A forme un anneau.

Démonstrations

• (1) => (2) :

Tout élément β de A[b] s'exprime comme l'image d'un polynôme Q[X] en b : β = Q[b]. Comme le polynôme minimal P[X] de b est unitaire, il est possible de réaliser une division euclidienne de Q[X] par P[X] et il existe deux polynôme D[X] et R[X] de A[X] tel que, si n désigne le degré de P[X] :

On remarque que P[b] est égal à 0 car P[X] est le polynôme minimal de b. On en déduit que β est égal à R[b], autrement dit β est combinaison linéaire de la famille : (1, b, ..., b_n-1). Cette famille est génératrice de A[b], comme elle est finie, la proposition (2) est établie.

• (2) => (3) :

Il suffit de choisir A[b] pour sous-algèbre C.

• (3) => (4) :

La sous-algèbre C est stable par multiplication par b car b est un élément de C, C contient 1 : un élément qui n'est pas diviseur de zéro. Enfin elle possède une famille génératrice finie par hypothèse. Il suffit de choisir C comme sous-A module D.

• (4) => (1) :

Soit (d_j) pour j variant de 1 à n une famille génératrice G de D. Pour tout j, b.d_j est un élément de D et s'exprime comme une combinaison linéaire de G à coefficients dans A :

Hélas, la matrice (a_ij) ne peut être considérée comme celle de φ_b, l'endomorphisme de D qui à x associe b.x. La famille G n'est pas nécessairement libre. Considérons l'endomorphisme α de Aⁿ de matrice (a_ij) dans sa base canonique et γ l'application linéaire de Aⁿ dans D qui, à la base canonique de Aⁿ associe la famille G. On a l'égalité :

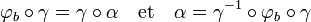
Notons χ[X] le polynôme caractéristique de α. Le théorème de Cayley-Hamilton montre qu'il annule α, on en déduit que :

Il existe un élément c qui n'est pas diviseur de zéro. il s'exprime comme combinaison linéaire de la famille G, soit (c_j) les coefficients de cette combinaison linéaire et p_i le coefficient du monôme de degré i de χ[X]:

Le fait que c ne soit pas diviseur de zéro montre que χ[X] est un polynôme annulant b, unitaire au facteur (-1)ⁿ près et à coefficients dans A. χ[X] est bien le polynôme minimal recherché.

 

Voir aussi

Notes

Liens externes

Galois

• (fr) Corps de nombres algébriques par S. Mehl
• (fr) Le théoreme fondamental de la théorie de Galois par B. le Stum Université de Rennes 1 2001
• (fr) Un cours de DEA sur la théorie de Galois par Alain Kraus Université de Paris VI 1998
• (fr) Trace, formes quadratiques et extensions de corps par Y Coudene de l'Université de Renne 1 2003

Arithmétique

• (fr) Cours de maîtrise de mathématiques : Théorie algébrique des nombres B. Edixhoven, L. Moret-Bailly Université de Rennes 1
• (fr) Sur l'arithmétique du corps de tous les nombres algébriques par E. Cahen (1928)

Références

Galois

• (fr) R. et A. Douady Algèbre et théories galoisiennes Cassini 2005 — ISBN 2-84225-005-2
• (en) E. Artin Galois Theory Notre Dame Press, Londres 1971
• (en) J. Bewersdorff Galois Theory for Beginners: A Historical Perspective, AMS 2006

Arithmétique

• (fr) Pierre Samuel, Théorie algébrique des nombres [détail des éditions]
• (fr) Jean-Pierre Serre, Cours d'arithmétique [détail des éditions]
• (fr) Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808) [détail des éditions]

• Portail des mathématiques