Entier d'Eisenstein

Entier d'Eisenstein
Les entiers d'Eisenstein sont les points d'intersection d'un treillis triangulaire dans le plan complexe

En mathématiques, les entiers d'Eisenstein, nommés en l'honneur du mathématicien Gotthold Eisenstein, sont des nombres complexes de la forme

z = a + b\,\omega

où a et b sont des entiers et

\omega = \frac{1}{2}(-1 + i\sqrt{3}) = e^{2\pi \frac{i}{3}}

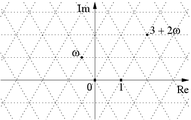
est une racine de l'unité cubique complexe. Les entiers d'Eisenstein forment un réseau triangulaire dans le plan complexe. Ils contrastent avec les entiers de Gauss qui forment un réseau carré dans le plan complexe. Ils correspondent à un exemple d'entiers quadratiques qui, comme toutes les fermetures intégrales d'une extension finie des nombres rationnels forme un anneau de Dedekind.

Les entiers d'Eisenstein sont utilisés en arithmétique modulaire pour la résolution d'équations diophantiennes, par exemple dans les démonstrations du dernier théorème de Fermat dans le cas où le paramètre est égal à 3. L'équation x2 + 3.y2 traitée dans l'article Théorème des deux carrés de Fermat possède aussi une méthode de résolution utilisant ces entiers.

Sommaire

Propriétés

Les entiers d'Eisenstein forment un anneau commutatif d'entiers algébriques dans le corps de nombres algébriques \mathbb{Q}(\sqrt{-3}\,). Ils forment aussi un anneau euclidien.

Pour voir que les entiers d'Eisenstein sont des entiers algébriques, notez que chaque z = a + b\,\omega\, est une racine du monôme

z^2 - (2a - b)z + (a^2 - ab + b^2)\,.

En particulier, \omega\, satisfait l'équation

\omega^2 + \omega + 1 = 0\,.

Le groupe des unités dans l'anneau d'Eisenstein est le groupe cyclique formé par les six racines de l'unité dans le plan complexe. Plus précisément, ce sont les suivantes :

{\pm\,1\, , \pm\,\omega\,, \pm\,\omega^2\,}

Celles-ci sont simplement les entiers d'Eisenstein de module égal à un.

Nombres premiers d'Eisenstein

Si x et y sont des entiers d'Eisenstein, nous disons que x divise y s'il existe un certain entier d'Eisenstein z tel que

y = z x\,.

Ceci étend la notion de divisibilité des entiers ordinaires. Par conséquent, nous pouvons aussi étendre la notion de primalité. Un entier d'Eisenstein non-unitaire x est dit nombre premier d'Eisenstein si ses seuls diviseurs sont de la forme ux et u où u est l'une des six unités.

Il peut être montré qu'un nombre premier ordinaire (ou nombre premier rationnel) qui est 3 ou congru à 1 mod 3 est de la forme x^2 - xy + y^2\, pour certains entiers x,y et peut être par conséquent factorisé en (x + \omega y)(x + \omega^2 y) \, et à cause de ceci, n'est pas premier dans les entiers d'Eisenstein. Les nombres premiers ordinaires congrus à 2 mod 3 ne peuvent pas être factorisés de cette manière et sont premiers dans les entiers d'Eisenstein. Aussi, un nombre de la forme x^2 - xy + y^2\, est un nombre premier rationnel ssi x + \omega\,y\, est un nombre premier d'Eisenstein.

Anneau euclidien

L'anneau des entiers d'Eisenstein forme un anneau euclidien de norme v égale à

v(a + \omega b) = a^2 - a b + b^2\,

Ceci peut être déduit en intégrant les entiers d'Eisenstein dans les nombres complexes. Puisque

v(a + i b) = a^2 + b^2\,

et puisque

a + \omega b = \left( a - {1\over 2}b\right) + i {\sqrt{3}\over 2} b

il s'ensuit que

v(a + \omega b) = \left( a - {1\over 2}b\right)^2 + {3\over 4} b^2
= a^2 - a b + {1\over 4}b^2 + {3\over 4}b^2 = a^2 - a b + b^2.

Voir aussi

Liens externes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Entier d'Eisenstein de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Entier De Gauss — Pour les articles homonymes, voir Entier (homonymie). Carl Friedrich Gauss. En mathématiques, et plus précisément en …   Wikipédia en Français

  • Entier de gauss — Pour les articles homonymes, voir Entier (homonymie). Carl Friedrich Gauss. En mathématiques, et plus précisément en …   Wikipédia en Français

  • Entier algébrique — Pour les articles homonymes, voir Entier (homonymie). En mathématiques, les entiers algébriques forment une famille de nombres qui généralise l ensemble des nombres entiers dits relatifs. Ils jouent un rôle analogue à ces derniers en théorie… …   Wikipédia en Français

  • Entier de Gauss — Pour les articles homonymes, voir Entier (homonymie). Carl Friedrich Gauss. En mathématiques, et plus précisément en théorie algébrique des nombres, un entier de …   Wikipédia en Français

  • Entier De Dirichlet — Pour les articles homonymes, voir Entier (homonymie). Dirichlet En mathématiques, et plus précisément en arithmétique modulai …   Wikipédia en Français

  • Entier de dirichlet — Pour les articles homonymes, voir Entier (homonymie). Dirichlet En mathématiques, et plus précisément en arithmétique modulai …   Wikipédia en Français

  • Entier Algébrique — Pour les articles homonymes, voir Entier (homonymie). En mathématiques, les entiers algébriques forment une famille de nombres qui généralise l ensemble des nombres entiers dits relatifs. Ils jouent un rôle analogue à ces derniers en théorie… …   Wikipédia en Français

  • Entier algebrique — Entier algébrique Pour les articles homonymes, voir Entier (homonymie). En mathématiques, les entiers algébriques forment une famille de nombres qui généralise l ensemble des nombres entiers dits relatifs. Ils jouent un rôle analogue à ces… …   Wikipédia en Français

  • Entier de Dirichlet — Pour les articles homonymes, voir Entier (homonymie). Dirichlet En mathématiques, et plus précisément en arithmétique modulaire, nous appellerons …   Wikipédia en Français

  • Entier quadratique — Pour les articles homonymes, voir Entier (homonymie). En mathématiques, un entier quadratique est un nombre réel ou complexe, racine d un polynôme du second degré à coefficients dans les nombres entiers et dont le coefficient du terme du plus… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”