Nombre Premier Régulier

Nombre Premier Régulier

Nombre premier régulier

En mathématiques, un nombre premier impair est dit régulier si une certaine propriété liée aux racines du polynôme xp-1 est vérifiée. Cette notion a été introduite par Ernst Kummer, pour une preuve du grand théorème de Fermat en 1847[1], dans un article intitulé Beweis des Fermat'schen Satzes der Unmöglichkeit von xl+yl=zl für eine unendliche Anzahl Primzahlen l'.

Plusieurs formulations équivalentes sont possibles pour définir la régularité d'un nombre premier. L'une d'entre elles est que le nombre premier p ne doit pas être un diviseur du nombre de classes (c'est-à-dire du cardinal du groupe des classes) du corps cyclotomique 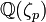\mathbb{Q}(\zeta_p), où ζp est une racine primitive p-ème de l'unité. Une manière de tester l'irrégularité en pratique est donnée par la caractérisation suivante : le nombre premier p est régulier si et seulement s'il ne divise le numérateur d'aucun des nombres de Bernoulli Bk, pour k prenant les valeurs paires entre 2 et p-3.

Les plus petits nombres premiers irréguliers sont 37, 59, 67, 101. Il est connu qu'il existe une infinité de nombres premiers irréguliers, mais l'existence d'une infinité de nombres premiers réguliers reste une question ouverte.

Le travail de Kummer permet précisément de montrer l'assertion suivante : si p est un nombre premier régulier, l'équation xp+yp=zp n'a pas de solutions pour x, y et z entiers relatifs tous non divisibles par p. Le point central de l'argument, développé en termes modernes, est qu'une telle identité se factorise en :

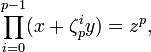
\prod_{i=0}^{p-1}(x+\zeta_p^iy)=z^p,

dans le corps 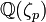\mathbb{Q}(\zeta_p). Cette égalité peut alors être interprétée comme une égalité entre le produit des idéaux 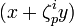(x+\zeta_p^iy) et l'idéal (z) élevé à la puissance p. Il peut être montré que les idéaux 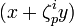(x+\zeta_p^iy) sont premiers entre eux, la théorie de la décomposition des idéaux premiers, et celle des anneaux de Dedekind permet d'assurer que chacun est la puissance p-ème d'un certain autre idéal Ai ; l'idéal Aip est principal, l'hypothèse que le nombre p est régulier (il n'est pas diviseur du nombre de classes de 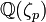\mathbb{Q}(\zeta_p)), montre alors que l'idéal Ai lui-même est principal, ce qui fournit une égalité de la forme 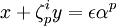x+\zeta_p^iy=\epsilon\alpha^p, pour une certaine unité ε. Quelques calculs permettent d'aboutir à une contradiction.

Notes et références

  1. ↑ (en) Lawrence C. Washington, Introduction to cyclotomic fields [détail des éditions], notes du chapitre 1.

Bibliographie

  • (en) Lawrence C. Washington, Introduction to cyclotomic fields [détail des éditions]
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Nombre premier r%C3%A9gulier ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre Premier Régulier de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Nombre premier regulier — Nombre premier régulier En mathématiques, un nombre premier impair est dit régulier si une certaine propriété liée aux racines du polynôme xp 1 est vérifiée. Cette notion a été introduite par Ernst Kummer, pour une preuve du grand théorème de… …   Wikipédia en Français

  • Nombre premier régulier — En mathématiques, un nombre premier impair est dit régulier si une certaine propriété liée aux racines du polynôme xp 1 est vérifiée. Cette notion a été introduite par Ernst Kummer, pour une preuve du Dernier théorème de Fermat en 1847[1], dans… …   Wikipédia en Français

  • Nombre premier irrégulier — Nombre premier régulier En mathématiques, un nombre premier impair est dit régulier si une certaine propriété liée aux racines du polynôme xp 1 est vérifiée. Cette notion a été introduite par Ernst Kummer, pour une preuve du grand théorème de… …   Wikipédia en Français

  • Nombre Premier — 7 est un nombre premier car il admet exactement deux diviseurs positifs …   Wikipédia en Français

  • Nombre premier — 7 est un nombre premier car il admet exactement deux diviseurs positifs. Un nombre premier est un entier naturel qui admet exactement deux diviseurs distincts entiers et positifs (qui sont alors 1 et lui même). Cette définition exclut 1, qui n a… …   Wikipédia en Français

  • Nombre premier de Fermat — Nombre de Fermat Pierre de Fermat étudie les propriétés des nombres portant maintenant son nom. Un nombre de Fermat est un entier naturel qui peut s écrire sous la forme 22n + 1, avec n entier. Le ne nombre de Fermat, 22n + 1, est noté Fn. Ces… …   Wikipédia en Français

  • Nombre premier de Pierpont — Un nombre premier de Pierpont est un nombre premier de la forme pour u et v deux entiers positifs. Ils sont nommés ainsi d après le mathématicien James Pierpont. Il est possible de prouver que si v = 0 et u > 0, alors u doit être une puissance …   Wikipédia en Français

  • Nombre de classes — Groupe des classes d idéaux En mathématiques, la théorie des corps de nombres fait apparaître un groupe abélien fini construit à partir de chaque tel corps : son groupe des classes d idéaux. Sommaire 1 Histoire et origine du groupe des… …   Wikipédia en Français

  • Nombre de Bernoulli — En mathématiques, les nombres de Bernoulli, notés (ou parfois , pour ne pas les confondre avec les polynômes de Bernoulli ou avec les nombres de Bell), constituent une suite de nombres rationnels. Les premiers nombres de Bernoulli sont donnés par …   Wikipédia en Français

  • Nombre De Fermat — Pierre de Fermat étudie les propriétés des nombres portant maintenant son nom. Un nombre de Fermat est un entier naturel qui peut s écrire sous la forme 22n + 1, avec n entier. Le ne nombre de Fermat, 22n + 1, est noté Fn. Ces nombres doivent… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”