Loi de Poisson

Pour les articles homonymes, voir Poisson (homonymie).

Poisson
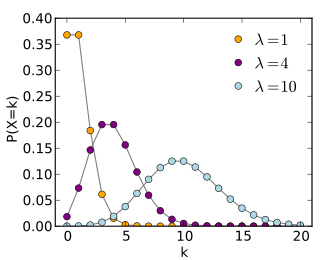
Densité de probabilité / Fonction de masse L'axe horizontal est l'indice k. La fonction est seulement définie pour les valeurs entières de k.
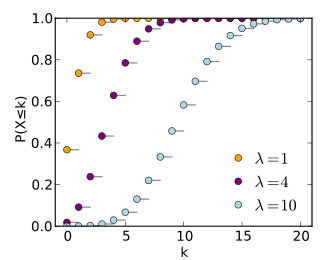
Fonction de répartition L'axe horizontal est l'indice k. La fonction de répartition est seulement discontinue pour les valeurs entières de k.

Paramètres	$\lambda \in{} ]0,+\infty[$ ^[1]
Support	$k \in \N$
Densité de probabilité (fonction de masse)	$\frac{e^{-\lambda} \lambda^k}{k!}\!$
Fonction de répartition	$\frac{\Gamma(\lfloor k+1\rfloor, \lambda)}{\lfloor k\rfloor !}\!\text{ pour }k\ge 0$ (où $Γ(x, y)$ est la Fonction gamma incomplète)
Espérance	$\lambda\,$
Médiane (centre)	$\text{environ }\lfloor\lambda+1/3-0.02/\lambda\rfloor$
Mode	$\lceil\lambda\rceil-1$
Variance	$\lambda\,$
Asymétrie	$\lambda^{-1/2}\,$
Kurtosis normalisé	$\lambda^{-1}\,$
Entropie	$\lambda[1\!-\!\log(\lambda)]\!+\!e^{-\lambda}\sum_{k=0}^\infty \frac{\lambda^k\log(k!)}{k!}.$ Pour $λ$ grand : $\scriptstyle\frac{1}{2}\log(2 \pi e \lambda) - \frac{1}{12 \lambda} - \frac{1}{24 \lambda^2} - \frac{19}{360 \lambda^3} + O\left(\frac{1}{\lambda^4}\right)$
Fonction génératrice des moments	$\exp(\lambda (e^t-1))\,$
Fonction caractéristique	$\exp(\lambda (e^{it}-1))\,$
modifier

En théorie des probabilités et en statistiques, la loi de Poisson est une loi de probabilité discrète qui décrit le comportement du nombre d'évènements se produisant dans un laps de temps fixé, si ces évènements se produisent avec une fréquence moyenne connue et indépendamment du temps écoulé depuis l'évènement précédent. La loi de Poisson est également pertinente pour décrire le nombre d'évènements dans d'autres types d'intervalles, spatiaux plutôt que temporels, comme des segments, surfaces ou volumes.

La loi de Poisson a été introduite en 1838 par Siméon-Denis Poisson (1781–1840), dans son ouvrage Recherches sur la probabilité des jugements en matière criminelle et en matière civile [1]. Le sujet principal de cet ouvrage consiste en certaines variables aléatoires N qui dénombrent, entre autres choses, le nombre d'occurrences (parfois appelées “arrivées”) qui prennent place pendant un laps de temps de longueur donnée.

Si le nombre moyen d'occurrences dans cet intervalle est λ, alors la probabilité qu'il existe exactement k occurrences (k étant un entier naturel, k = 0, 1, 2, ...) est

$p(k) = P(X = k)= \mathrm{e}^{-\lambda}\frac{\lambda ^k}{k!}\,$

où

e est la base de l'exponentielle (2,718...)
k! est la factorielle de k
λ est un nombre réel strictement positif^[1].

On dit alors que X suit la loi de Poisson de paramètre λ.

Par exemple, si un certain type d'évènements se produit en moyenne 4 fois par minute, pour étudier le nombre d'évènements se produisant dans un laps de temps de 10 minutes, on choisit comme modèle une loi de Poisson de paramètre λ = 10× 4 = 40.

Sommaire

1 Calcul de p(k)
2 Espérance, variance, écart type, fonctions génératrices
3 Domaine d'application
- 3.1 Lien avec la loi de Bernoulli
4 Diagrammes en bâtons
5 Stabilité de la loi de Poisson par la somme
6 En littérature
7 Notes et références
8 Voir aussi
- 8.1 Articles connexes

Calcul de p(k)

Ce calcul peut se faire de manière déductive en travaillant sur une loi binomiale de paramètres (T; λ/T). Pour T grand, on démontre que la loi binomiale converge vers la loi de Poisson.

Il peut aussi se faire de manière inductive en étudiant sur l'intervalle [0; T] les fonctions $F k (t)$ = probabilité que l'événement se produise k fois sur l'intervalle de temps [0 ; t]. En utilisant la récurrence et du calcul différentiel, on parvient à retrouver les formules précédentes.

Espérance, variance, écart type, fonctions génératrices

L'espérance d'une loi de Poisson est $λ.$
La variance d'une loi de Poisson est également $λ.$
Son écart type est donc $\sqrt{\lambda}.$
La fonction génératrice de la loi de Poisson est

$G_{X} (t) =\ e^{\lambda(t-1)}.$

La fonction génératrice des moments d'une loi de Poisson est

$M_{X}(t)\equiv \mathbb{E}(e^{tX})=\exp\left(\lambda (e^t-1)\right).$

Démonstration

Espérance

Si $X\,$ suit une loi de poisson de paramètre $\lambda\,$ , soit $X \sim \mathcal{P}(\lambda)\,$ .

Alors, on a par définition que $\mathbb{P}(X=k)=e^{-\lambda}\frac{\lambda^k}{k!}$ et que:

$\begin{align}\mathbb{E}(X) &= \sum_{k=1}^{+{\infty}}k\,\mathbb{P}(X=k)\\&=\sum_{k=1}^{+{\infty}}k\,e^{-\lambda}\frac{\lambda^k}{k!}\\&=e^{-\lambda}\,\sum_{k=1}^{+{\infty}}\frac{\lambda^k}{(k-1)!}\\&=\lambda\,e^{-\lambda}\,\sum_{k=1}^{+{\infty}}\frac{\lambda^{k-1}}{(k-1)!}&=\lambda\,e^{-\lambda}\,e^{\lambda}\,=\lambda\end{align}$

Dans la dernière ligne, on reconnaît le développement en série entière de $e^{x}\,$ .

Variance

$\begin{align}V(X) &= \mathbb{E}(X^2) - ( \mathbb{E}(X) ) ^2\\ &= \sum_{k=1}^{+{\infty}}k^2\,\mathbb{P}(X=k) - \lambda^2\\ &= \sum_{k=1}^{+{\infty}}k^2\,e^{-\lambda}\frac{\lambda^k}{k!} - \lambda^2\\ &= \lambda\,e^{-\lambda} \sum_{k=1}^{+{\infty}}\,\frac{k\lambda^{k-1}}{(k-1)!} - \lambda^2\\ &= \lambda\,e^{-\lambda} \sum_{k=1}^{+{\infty}}\,\frac{d}{d\lambda}\frac{\lambda^k}{(k-1)!} - \lambda^2\\ &= \lambda\,e^{-\lambda} \frac{d}{d\lambda} \sum_{k=1}^{+{\infty}}\,\frac{\lambda^k}{(k-1)!} - \lambda^2\\ &= \lambda\,e^{-\lambda} \frac{d}{d\lambda}[\lambda\sum_{k=1}^{+{\infty}}\,\frac{\lambda^{k-1}}{(k-1)!}] - \lambda^2\\ &= \lambda\,e^{-\lambda} \frac{d}{d\lambda}[\lambda\,e^{\lambda}] - \lambda^2 \qquad \qquad \text{ car } \exp(x) = \sum_{n = 0}^{+\infty} {x^n \over n!}\\ &= \lambda\,e^{-\lambda}(\lambda+1)\,e^{\lambda} - \lambda^2\\ &= \lambda\,(\lambda+1) - \lambda^2\\ &= \lambda\,\end{align}$

Fonction génératrice

La fonction génératrice d'une variable aléatoire X est définie par $G_{X} (t) =\ \mathbb{E}(t^X).$ Ainsi on obtient :

$\begin{align}\mathbb{E}(t^X) &= \sum_{k=0}^{\infty} t^k \mathbb{P}(X=k)\\ &= \sum_{k=0}^{\infty} t^k e^{-\lambda} \frac{\lambda^k}{k!}\\ &= e^{-\lambda}\sum_{k=0}^{\infty} t^k \frac{\lambda^k}{k!}\\ &= e^{-\lambda}\sum_{k=0}^{\infty} \frac{(t\lambda)^k}{k!}\\ &= e^{-\lambda} e^{t\lambda} \qquad \qquad \text{ car } \exp(x) = \sum_{n = 0}^{+\infty} {x^n \over n!}\\ &= e^{\lambda(t - 1)}\end{align}$

Fonction génératrice des moments

$\begin{align} M_{X}(t) &= \sum_{k=0}^{+\infty}\mathrm{e}^{tk}\mathbb{P}(X=k)\\ &= \sum_{k=0}^{+\infty}\mathrm{e}^{tk}\frac{\lambda^{k}}{k!}\,\mathrm{e}^{-\lambda}\\ &= \mathrm{e}^{-\lambda} \sum_{k=0}^{+\infty} \frac{(\lambda\, \mathrm{e}^{t})^{k}}{k!}\\ &= \mathrm{e}^{-\lambda} \mathrm{e}^{\lambda\, \mathrm{e}^{t}} \qquad \qquad \text{ car } \exp(x) = \sum_{n = 0}^{+\infty} {x^n \over n!}\\ &= \mathrm{e}^{\lambda(\mathrm{e}^{t}-1)} \end{align}$

Domaine d'application

Le domaine d'application de la loi de Poisson a été longtemps limité à celui des événements rares comme les suicides d'enfants, les arrivées de bateaux dans un port ou les accidents dus aux coups de pied de cheval dans les armées (étude de Ladislaus Bortkiewicz).

Mais depuis quelques décennies son champ d'application s'est considérablement élargi. Actuellement, on l'utilise beaucoup dans les télécommunications (pour compter le nombre de communications dans un intervalle de temps donné), le contrôle de qualité statistique, la description de certains phénomènes liés à la désintégration radioactive (la désintégration des noyaux radioactifs suivant, par ailleurs, une loi exponentielle de paramètre noté aussi lambda), la biologie (mutations), la météorologie, la finance pour modéliser la probabilité de défaut d'un crédit…

Lien avec la loi de Bernoulli

Le décompte des évènements rares se fait souvent au travers d'une somme de variables de Bernoulli, la rareté des évènements se traduisant par le fait que les paramètres de ces variables de Bernoulli sont petits (ainsi, la probabilité que chaque évènement survienne est faible). Le lien entre la loi de Poisson et les évènements rares peut alors s'énoncer ainsi :

Paradigme de Poisson — La somme S_n d'un grand nombre de variables de Bernoulli indépendantes de petit paramètre suit approximativement la loi de Poisson de paramètre $\scriptstyle\ \mathbb{E}[S_n]. \$

L'inégalité de Le Cam précise le paradigme de Poisson : soit $\scriptstyle\ X_{1,n}, X_{2,n},\dots, X_{a_n,n}\$ un tableau de variables aléatoires de Bernoulli indépendantes, avec paramètres respectifs $\scriptstyle\ p_{k,n}.\$ On note

$S_n=\sum_{k=1}^{a_n}\,X_{k,n}\quad\text{et}\quad\lambda_n\ =\ \mathbb{E}[S_n]=\sum_{k=1}^{a_n}\,p_{k,n}.\$

Inégalité de Le Cam^[2] — Pour tout ensemble A d'entiers naturels,

$\left|\mathbb{P}\left(S_n\in A\right)-\sum_{k\in A}\,\frac{\lambda_n^k\,e^{-\lambda_n}}{k!}\right|\ \le\ \sum_{k=1}^{a_n}\,p_{k,n}^2.$

En particulier, si les deux conditions suivantes sont réunies :

$\lim_n \lambda_n\,=\,\lambda>0,\$
$\lim_n \sum_{k=1}^{a_n}\,p_{k,n}^2\,=\,0,\$

alors S_n converge en loi vers la loi de Poisson de paramètre λ.

Dans l'énoncé du paradigme de Poisson, on fait deux hypothèses (vagues) sur les termes d'une somme S_n de variables de Bernoulli :

les paramètres des variables de Bernoulli sont petits ; or les deux conditions ci-dessus entrainent que

$\lim_n \max_{1\le k\le a_n}\,p_{k,n}\,=\,0,\$

il y a un grands nombre de termes ; or les deux conditions ci-dessus entrainent que

$\lim_n a_n\,=\,+\infty.\$

Remarques :

Ce paradigme reste pertinent, dans certaines conditions, si l'on relaxe l'hypothèse d' indépendance^[3].
- Un exemple frappant est le nombre de points fixes d'une permutation tirée au hasard.
- Un autre exemple est le nombre de points isolés du graphe aléatoire, dont la convergence vers la loi de Poisson a permis à Erdös et Rényi de démontrer, en 1960, le théorème double-exponentiel.
Le cas particulier a_n=n, p_k,n=λ/n, λ_n=λ, de l'inégalité de Le Cam, précise la rapidité de convergence de la loi binomiale de paramètres n et λ/n vers la loi de Poisson de paramètre λ.

Diagrammes en bâtons

Comme toute loi de probabilité discrète, une loi de Poisson peut être représentée par un diagramme en bâtons. Ci-dessous sont représentés les diagrammes en bâtons des lois de Poisson de paramètres 1, 2 et 5.

diagramme en bâtons d'une loi de Poisson de paramètre 1

Lorsque le paramètre λ de la loi de Poisson devient grand, (pratiquement lorsqu'il est supérieur à 5), son diagramme en bâton est correctement approché par l'histogramme d'une loi normale d'espérance et de variance égales à λ (l'intervalle de classe étant égal à l'unité). Cette convergence était mise à profit, avant que les moyens informatiques ne se généralisent, pour utiliser la loi normale en lieu et place de la loi de Poisson dans certains tests.

Stabilité de la loi de Poisson par la somme

Si X et Y sont deux variables aléatoires indépendantes qui suivent des lois de Poisson de paramètres λ et μ, alors X+Y est une variable aléatoire qui suit la loi de Poisson de paramètre λ + μ.

Théorème — Si $X\sim \mathcal{P}(\lambda)$ et $Y \sim \mathcal{P}(\mu)$ sont indépendantes, alors $X+Y \sim \mathcal{P}(\lambda+\mu)$

Démonstration

La démonstration est faite ici par la fonction génératrice des moments. On sait en effet que $M X + Y (t) = M X (t) M Y (t)$ par indépendance de X et Y et que la fonction génératrice des moments détermine univoquement la loi.

En partant du résultat démontré plus haut: $M X (t) = exp(λ(e t - 1))$ ,

on calcule: $M X + Y (t) = M X (t) M Y (t) = exp(λ(e t - 1))exp(μ(e t - 1)) = exp(λ(e t - 1) + μ(e t - 1)) = exp((λ + μ)(e t - 1))$

Le résultat

M X + Y (t) = exp((λ + μ)(e t - 1))

est simplement la fonction génératrice des moments d'une loi de Poison de paramètre

λ + μ

En littérature

Dans le roman de Thomas Pynchon, L'Arc-en-ciel de la gravité, un des personnages, le statisticien Roger Mexico, utilise la loi de Poisson pour cartographier les zones d'impact des fusées allemandes V2 sur la ville de Londres durant la bataille d'Angleterre.

Notes et références

↑ ^{a et b} Avec les conventions habituelles 0!=1 et 0⁰=1, la définition de la loi de Poisson s'étend à λ=0 : on trouve alors p(0)=1 et, dès que k>0, p(k)=0. Ainsi une variable aléatoire nulle presque sûrement peut être vue comme suivant la loi de Poisson de paramètre 0. Cette convention est cohérente avec les propriétés essentielles de la loi de Poisson de paramètre strictement positif. Elle est commode, voire indispensable, par exemple lors de l'étude des processus ponctuels de Poisson.
↑ L. Le Cam, « An Approximation Theorem for the Poisson Binomial Distribution », dans Pacific Journal of Mathematics, vol. 10, n^o 4, 1960, p. 1181–1197 [texte intégral (page consultée le 2009-05-13)]
↑ (en) A. D. Barbour, L. Holst et S. Janson, Poisson approximation, The Clarendon Press Oxford University Press, 1992 (ISBN 0198522355) .

Voir aussi

Sur les autres projets Wikimedia :

« Table de la loi de Poisson », sur Wikisource (bibliothèque universelle)

Articles connexes

v · Lois de probabilités

Lois discrètes

à support fini	Loi de Bernoulli • Loi uniforme discrète • Loi binomiale • Loi hypergéométrique • Loi de Benford
à support dénombrable	Loi géométrique • Loi de Poisson • Loi binomiale négative • Loi logarithmique

Lois continues

à support compact	Loi uniforme continue • Loi triangulaire • Loi bêta
à support semi-infini	Loi exponentielle • Loi Gamma • Loi du χ² • Loi de Fisher • Loi de Weibull • Loi de Rayleigh • Loi de Rice • Loi d'Erlang • Loi de Lévy • Loi inverse-gamma • Loi log-normale
à support infini	Loi normale • Loi normale asymétrique • Loi de Cauchy • Loi de Laplace • Loi logistique • Loi de Student • Loi stable • Loi de Gumbel

v · Probabilités et statistiques

Théorie des probabilités

Axiomes des probabilités • Espace probabilisable • Probabilité • Événement • Tribu • Indépendance

Probabilités élémentaires	Moyenne • Espérance • Médiane • Variance • Écart type
Loi de probabilité	Variable aléatoire • Loi de Poisson • Loi normale • Loi de Student • Loi de Fisher • Variables iid
Convergence de variables aléatoires	Théorème central limite • Loi des grands nombres
Processus stochastique	Marche aléatoire • Chaîne de Markov • Processus de Markov • Mouvement brownien • Équation différentielle stochastique

Statistiques

Statistique descriptive	Échantillon • Quantile • Intervalle de confiance • Représentations de données • Histogramme • Diagramme circulaire • Boîte à moustaches • Régression linéaire • Méthode des moindres carrés
Statistique mathématique	Fonction de répartition empirique • Théorème de Glivenko-Cantelli • Inférence bayésienne
Tests statistiques	Test d'hypothèse • Hypothèse statistique • Estimateur • Test du χ² • Test t • Test de Fisher

Applications

Économétrie • Mécanique statistique • Jeu de hasard • Biomathématique • Mathématiques financières

Portail des probabilités et des statistiques

Catégorie :

Loi de probabilité

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi de Poisson de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Loi De Poisson — Pour les articles homonymes, voir Poisson (homonymie). Poisson Densité de probabilité / Fonction de masse … Wikipédia en Français
Loi de poisson — Pour les articles homonymes, voir Poisson (homonymie). Poisson Densité de probabilité / Fonction de masse … Wikipédia en Français
loi de Poisson — ● loi de Poisson Loi de probabilité d une variable aléatoire discrète prenant des valeurs entières 0, 1, 2…, et dont la fonction de distribution est . (λ est le paramètre de la loi. Espérance mathématique et variance sont égales à λ.) … Encyclopédie Universelle
Loi De Probabilité — Une loi de probabilité ou distribution de probabilité a commencé par décrire les répartitions typiques des fréquences d apparition des résultats d un phénomène aléatoire. Dans le dernier quart du XXe siècle, on a largement étendu le concept… … Wikipédia en Français
Loi de probabilite — Loi de probabilité Une loi de probabilité ou distribution de probabilité a commencé par décrire les répartitions typiques des fréquences d apparition des résultats d un phénomène aléatoire. Dans le dernier quart du XXe siècle, on a largement … Wikipédia en Français
Loi Binomiale — Binomiale Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi binômiale — Loi binomiale Binomiale Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
POISSON (S. D.) — POISSON SIMÉON DENIS (1781 1840) Mathématicien français dont les travaux portent sur les intégrales définies, la théorie électromagnétique et le calcul des probabilités. Siméon Denis Poisson est né à Pithiviers; sa famille le força à faire des… … Encyclopédie Universelle
Loi log-normale — Densité de probabilité / Fonction de masse μ=0 Fonction de répartition μ=0 … Wikipédia en Français
Loi logistique — Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Loi de Poisson

Sommaire

Calcul de p(k)