Loi binomiale

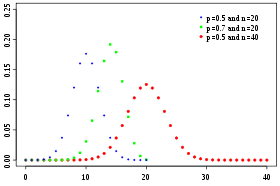
Binomiale
Densité de probabilité / Fonction de masse
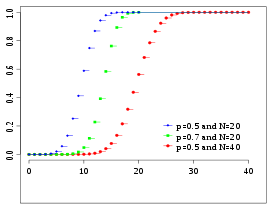
Fonction de répartition

Paramètres	$n \geq 0$ nombre d'épreuves (entier) $0\leq p \leq 1$ probabilité de succès (réel) $q = 1 - p$
Support	$k \in \{0,\dots,n\}\!$
Densité de probabilité (fonction de masse)	${n\choose k} p^k q^{n-k} \!$
Fonction de répartition	$I_{1-p}(n-\lfloor k\rfloor, 1+\lfloor k\rfloor) \!$
Espérance	$np\!$
Médiane (centre)	un des $\{\lfloor np\rfloor, \lceil np \rceil\}$ ^[1]
Mode	$\lfloor (n+1)\,p\rfloor\!$
Variance	$npq\!$
Asymétrie	$\frac{q-p}{\sqrt{npq}}\!$
Kurtosis normalisé	$\frac{1-6pq}{npq}\!$
Entropie	$\frac{1}{2} \ln \left( 2 \pi n e p q \right) + O \left( \frac{1}{n} \right)$
Fonction génératrice des moments	$(q + pe^t)^n \!$
Fonction caractéristique	$(q + pe^{it})^n \!$
modifier

En mathématiques, une loi binomiale de paramètres n et p est une loi de probabilité qui correspond à l'expérience suivante :

On renouvelle n fois de manière indépendante une épreuve de Bernoulli de paramètre p (expérience aléatoire à deux issues possibles, généralement dénommées respectivement « succès » et « échec », la probabilité d'un succès étant p, celle d'un échec étant $q = (1 - p)$ ). On compte alors le nombre de succès obtenus à l'issue des n épreuves et on appelle X la variable aléatoire correspondant à ce nombre de succès.

L'univers $X(\Omega )~$ désigne l'ensemble des entiers naturels de 0 à n.

La variable aléatoire suit une loi de probabilité définie par :

$p(k) = P(X = k)= {n \choose k} \, p^k q^{n-k}$

Cette formule fait intervenir le nombre des combinaisons de k éléments parmi n, généralement notée ${n\choose k}$ ou $\mathrm{C}_{n}^{k}$ , la première notation était préconisée en France pour l'enseignement des mathématiques en terminale scientifique^[2] jusque 2004. Notons que ce nombre de combinaisons se distingue du nombre des arrangements de k éléments parmi n, $A^k_n = \dfrac{n!}{(n-k)!}$ , du fait que dans une combinaison l'ordre des éléments n'importe pas. Et comme il y a k! (prononcer factorielle k) façons d'ordonner k éléments, le nombre des combinaisons se déduit du nombre des arrangements par la simple division $\dfrac{A^k_n}{k!}\,$ et on obtient :

${n\choose k} =\frac{n!}{k!(n-k)!}$

Cette loi de probabilité s'appelle la loi binomiale de paramètre (n ; p) et se note B(n ; p).

Calcul de p(k)

Une épreuve de Bernoulli conduit à la création d'un univers Ω = {S ; E}, (S pour Succès et E pour Echec).

n épreuves de Bernoulli indépendantes conduisent à la création d'un univers Ωⁿ constitué de n-uplets d'éléments de Ω, sur lequel peut se définir une probabilité produit. La probabilité de l'éventualité (S, S, ..., S, E, E, ..., E) avec k succès et n - k échecs a donc pour valeur $p k q n - k$ .

Plus généralement, tout n-uplet formé de k succès et de n-k échecs aura pour probabilité $p k q n - k$ quel que soit l'ordre d'apparition des S et des E.

L'évènement « X = k » est formé de tous les n-uplets comportant k succès et n - k échecs. La combinatoire permet de déterminer le nombre de n-uplets de ce type : il y en a autant que de parties à k éléments d'un ensemble à n éléments ; or chaque partie correspond à une façon de placer les k succès parmi les n places du n-uplet. Il y a donc ${n \choose k}$ n-uplets, chacun ayant une probabilité égale à $p k q n - k$ .

Donc $P(X = k) = {n \choose k} \, p^k (1-p)^{n-k} = {n \choose k} \, p^k q^{n-k}$ .

Lien avec la loi de Bernoulli

Du fait de son interprétation comme loi du nombre de succès lors d'une série de n épreuves de Bernoulli indépendantes et identiques, la loi binomiale est en particulier la loi de la somme de n variables aléatoires indépendantes suivant toutes la (même) loi de Bernoulli de paramètre p, prenant la valeur 1 en cas de succès (probabilité p) et 0 en cas d'échec (probabilité (1-p)). Des exemples importants où la loi binomiale apparaît comme loi de la somme de variables de Bernoulli sont les suivants :

l'étude des sondages,
la fonction de répartition empirique,
la fonction de répartition d'une statistique d'ordre, comme par exemple la médiane d'un échantillon, ou un quartile,
l'étude, par Émile Borel, de la fréquence des différents chiffres dans le développement décimal d'un nombre réel, et sa démonstration du Théorème des nombres normaux^[3].

Par ailleurs, cette interprétation en termes de sommes de variables de Bernoulli permet un calcul rapide de l'espérance et de la variance.

Espérance, variance, écart type

Ainsi X a la même loi que la somme S de n variables aléatoires indépendantes suivant toutes la (même) loi de Bernoulli de paramètre p. Comme l'espérance et la variance d'une variable aléatoire ne dépendent que de sa loi de probabilité, on en déduit que

E[X] est donc la somme des espérances de ces variables de Bernoulli, or elles ont pour espérance p et pour variance p(1-p), soit E[X]=np
de même, V(X) est la somme des variances de n variables de Bernoulli, soit V(X)=np(1-p)
$\sigma_{X} = \sqrt{np(1-p)}$

Convergence

Pour de grandes valeurs de n, le calcul de ${n \choose k} \, p^k q^{n-k}$ devient vite pratiquement impossible, sauf si l'on cherche à calculer le logarithme de cette expression au lieu de l'expression elle-même (et à condition d'utiliser l'approximation des factorielles par la formule de Stirling). On distingue deux cas :

Lorsque n tend vers l'infini et que p tend vers 0 avec np = a, la loi binomiale converge vers une loi de Poisson de paramètre a. En pratique, on remplace la loi binomiale par une loi de Poisson dès que n > 30 et np < 5 ou dès que n > 50 et p < 0.1.

Démonstration de la convergence vers la loi Poisson

Décomposons ${n \choose k} \, p^k q^{n-k} = {n \choose k} \, p^k (1-p)^{n-k}$

${n \choose k} \, p^k (1-p)^{n-k} = \frac{n(n-1)...(n-k+1)}{k!}p^k(1-p)^{n-k} = \frac{(pn)^{k}}{k!}(1-\frac{1}{n})(1-\frac{2}{n})...(1-\frac{k-1}{n})(1-p)^{n-k}$

On se place dans la situation où np reste constant et où n tend vers l'infini (par conséquent p tend vers 0).

Lorsque n tend vers l'infini, les termes $(1-\frac{1}{n})(1-\frac{2}{n})...(1-\frac{k-1}{n})$ tendent vers 1. Le produit des termes tend également vers 1 puisqu'ils sont en nombre fini.
On a (1 − p)^{n − k} = (1 − p)ⁿ(1 − p) ^{− k}
- Or $\lim_{p \to 0}(1-p)^{-k} = 1$
- De plus, $(1-p)^{n} = (1-\frac{np}{n})^n$ et ce terme tend vers e^-np quand n tend vers l'infini.

On trouve donc ${n \choose k} \, p^k (1-p)^{n-k} \rightarrow \frac{(np)^k}{k!}e^{-np}$ .

Il s'agit de la loi de probabilité d'une loi de Poisson de paramètre λ = np.

Pour n assez grand, la loi binomiale se comporte comme une loi normale gaussienne d'espérance np et de variance npq. Plus précisément, le théorème de Moivre-Laplace précise que si $Φ$ est la fonction de répartition de la loi normale centrée réduite $\mathcal{N}(0,1)$ et si $X_n\,$ suit une loi binomiale de paramètres n et p, on a alors, pour tout réel $\scriptstyle t$ :

$\lim_{n\to\infty}\operatorname{P} \left( \frac{X_n- np}{\sqrt{npq}}\leq t \right) = \Phi(t)$

Le théorème de Berry–Esseen (en) fournit une majoration de l'erreur commise quand on remplace $\operatorname{P}(X_n \le x)$ par $\operatorname{P}(Y_n \le x)$ où

Y n

suit une loi normale d'espérance np et de variance npq : l'erreur commise est inférieure à $\scriptstyle \dfrac C{\sqrt{npq}}$ où C <0,4784.

En pratique, on remplace une loi binomiale par une loi normale pour n grand et p pas trop proche de 0 ni de 1 (par exemple pour n > 30, np > 5 et nq > 5 ou pour npq>9)

Loi des grands nombres

La loi binomiale, son espérance et sa variance, ainsi que l'inégalité de Bienaymé-Tchebychev permettent de démontrer une version simple de la loi des grands nombres.

Références

↑ Hamza, K. (1995). The smallest uniform upper bound on the distance between the mean and the median of the binomial and Poisson distributions. Statist. Probab. Lett. 23 21–25.
↑ Bulletin Officiel n°4 du 30 aout 2001.
↑ Émile Borel, « Les probabilités dénombrables et leurs applications arithmétiques », dans Rendiconti del Circolo Matematico di Palermo, vol. 27, n^o 1, décembre 1909, p. 247-271 (ISSN 0009-725X et 1973-4409) [texte intégral, lien DOI] .

Voir aussi

Lien externe

v · Lois de probabilités

Lois discrètes

à support fini	Loi de Bernoulli • Loi uniforme discrète • Loi binomiale • Loi hypergéométrique • Loi de Benford
à support dénombrable	Loi géométrique • Loi de Poisson • Loi binomiale négative • Loi logarithmique

Lois continues

à support compact	Loi uniforme continue • Loi triangulaire • Loi bêta
à support semi-infini	Loi exponentielle • Loi Gamma • Loi du χ² • Loi de Fisher • Loi de Weibull • Loi de Rayleigh • Loi de Rice • Loi d'Erlang • Loi de Lévy • Loi inverse-gamma • Loi log-normale
à support infini	Loi normale • Loi normale asymétrique • Loi de Cauchy • Loi de Laplace • Loi logistique • Loi de Student • Loi stable • Loi de Gumbel

v · Probabilités et statistiques

Théorie des probabilités

Axiomes des probabilités • Espace probabilisable • Probabilité • Événement • Tribu • Indépendance

Probabilités élémentaires	Moyenne • Espérance • Médiane • Variance • Écart type
Loi de probabilité	Variable aléatoire • Loi de Bernoulli • Loi de Poisson • Loi uniforme • Loi normale • Loi de Student • Loi de Fisher • Variables iid
Convergence de lois	Théorème central limite • Loi des grands nombres • Théorème de Borel-Cantelli
Calcul stochastique	Marche aléatoire • Chaîne de Markov • Processus stochastique • Processus de Markov • Martingale • Mouvement brownien • Équation différentielle stochastique

Statistiques

Statistique descriptive	Échantillon • Quantile • Intervalle de confiance • Représentations de données • Histogramme • Diagramme circulaire • Boîte à moustaches • Régression linéaire • Méthode des moindres carrés
Statistique mathématique	Fonction de répartition empirique • Théorème de Glivenko-Cantelli • Inférence bayésienne
Tests statistiques	Test d’hypothèse • Hypothèse statistique • Estimateur • Test du χ² • Test t • Test de Fisher

Applications

Économétrie • Mécanique statistique • Jeu de hasard • Biomathématique • Mathématiques financières

Portail des probabilités et des statistiques

Catégorie :

Loi de probabilité

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi binomiale de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Loi Binomiale — Binomiale Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi binômiale — Loi binomiale Binomiale Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi binomiale — ● Loi binomiale loi théorique de distribution statistique telle que les fréquences soient égales aux coefficients binominaux … Encyclopédie Universelle
Loi binomiale négative — Binomiale négative Densité de probabilité / Fonction de masse La ligne rouge représente la moyenne et la ligne verte a pour longueur approximativement 2σ. Paramètres (réel) … Wikipédia en Français
Loi Normale — Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français
Loi Normale Reduite — Loi normale Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français
Loi de Gauss — Loi normale Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français
Loi de Laplace-Gauss — Loi normale Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français
Loi gaussienne — Loi normale Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français
Loi normale gaussienne — Loi normale Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Loi binomiale

Sommaire

Calcul de p(k)

Lien avec la loi de Bernoulli

Espérance, variance, écart type

Convergence

Loi des grands nombres

Références

Voir aussi

Lien externe

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Loi binomiale

Sommaire

Calcul de p(k)

Lien avec la loi de Bernoulli

Espérance, variance, écart type

Convergence

Loi des grands nombres

Références

Voir aussi

Lien externe

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link