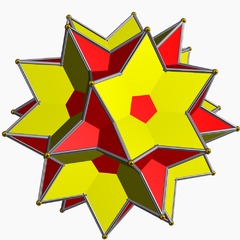
Grand icosidodecaedre
Contenu soumis à la licence CC-BY-SA. Source : Article Grand icosidodecaedre de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Grand Icosidodécaèdre — Type Polyèdre uniforme Éléments F=32, A=60, S=30 (χ=2) Faces par cotés 20{3}+12{5/2} Conf … Wikipédia en Français
Grand icosidodécaèdre — Type Polyèdre uniforme Éléments F=32, A=60, S=30 (χ=2) Faces par côtés 20{3}+12{5/2} Configuration de sommet … Wikipédia en Français
Grand Icosidodécaèdre Adouci — Type Polyèdre uniforme Éléments F=92, A=150, S=60 (χ=2) Faces par cotés (20+60){3}+12{5/2} … Wikipédia en Français
Grand Icosidodécaèdre Adouci Inversé — Grand icosidodécaèdre inversé adouci Type Polyèdre uniforme Éléments F=92, A=150, S=60 (χ=2) Faces par cotés (20+ … Wikipédia en Français
Grand Icosidodécaèdre Ditrigonal — Type Polyèdre uniforme Éléments F=32, A=60, S=20 (χ= 8) Faces par cotés 20{3}+12{5} … Wikipédia en Français
Grand Icosidodécaèdre Rétroadouci — Type Polyèdre uniforme Éléments F=92, A=150, S=60 (χ=2) Faces par cotés (20+60){3}+12{5 … Wikipédia en Français
Grand Icosidodécaèdre Tronqué — Type Polyèdre uniforme Éléments F=62, A=180, S=120 (χ=2) Faces par cotés 30{4}+20{6}+12{10/ … Wikipédia en Français
Grand icosidodecaedre adouci — Grand icosidodécaèdre adouci Grand icosidodécaèdre adouci Type Polyèdre uniforme Éléments F=92, A=150, S=60 (χ=2) Faces par cotés (20+60){3}+12{5/2} … Wikipédia en Français
Grand icosidodecaedre adouci inverse — Grand icosidodécaèdre adouci inversé Grand icosidodécaèdre inversé adouci Type Polyèdre uniforme Éléments F=92, A=150, S=60 (χ=2) Faces par cotés (20+ … Wikipédia en Français
Grand icosidodecaedre ditrigonal — Grand icosidodécaèdre ditrigonal Grand icosidodécaèdre ditrigonal Type Polyèdre uniforme Éléments F=32, A=60, S=20 (χ= 8) Faces par cotés 20{3}+12{5} … Wikipédia en Français