- Relativité générale
-
 Pour les articles homonymes, voir relativité.
Pour les articles homonymes, voir relativité.La relativité générale, fondée sur le principe de covariance générale qui étend le principe de relativité aux référentiels non-inertiels, est une théorie relativiste de la gravitation, c'est-à-dire qu'elle décrit l'influence sur le mouvement des astres de la présence de matière et, plus généralement d'énergie, en tenant compte des principes de la relativité restreinte. La relativité générale englobe et supplante la théorie de la gravitation universelle d'Isaac Newton qui en représente la limite aux petites vitesses (comparées à la vitesse de la lumière) et aux champs gravitationnels faibles.
La relativité générale est principalement l'œuvre d'Albert Einstein, dont elle est considérée comme la réalisation majeure, qu'il a élaborée entre 1907 et 1915. Les noms de Marcel Grossmann et de David Hilbert lui sont également associés, le premier ayant aidé Einstein à se familiariser avec les outils mathématiques nécessaires à la compréhension de la théorie (la géométrie différentielle), le second ayant franchi conjointement avec Einstein les dernières étapes menant à la finalisation de la théorie après que ce dernier lui eut présenté dans le courant de l'année 1915 les idées générales de sa théorie.
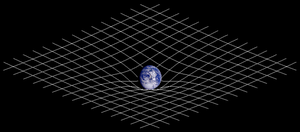
La relativité générale est fondée sur des concepts radicalement différents de ceux de la gravitation newtonienne. Elle énonce notamment que la gravitation n'est pas une force, mais est la manifestation de la courbure de l'espace (en fait de l'espace-temps), courbure elle-même produite par la distribution de l'énergie, sous forme de masse ou d'énergie cinétique, qui diffère suivant le référentiel de l'observateur[1]. Cette théorie relativiste de la gravitation donne lieu à des effets absents de la théorie newtonienne mais vérifiés, comme l'expansion de l'Univers, ou potentiellement vérifiables, comme les ondes gravitationnelles et les trous noirs. Elle ne permet pas de déterminer certaines constantes ou certains aspects de l'univers (notamment son évolution, s'il est fini ou non, etc) : des observations sont nécessaires pour préciser des paramètres ou faire des choix entre plusieurs possibilités laissées par la théorie.
Aucun des nombreux tests expérimentaux effectués à ce jour (2009) n'a pu la mettre en défaut[2]. Toutefois, des questions restent sans réponse : principalement sur le plan théorique, comment la relativité générale et la physique quantique peuvent être unies pour produire une théorie complète et cohérente de gravité quantique[3] ; et sur le plan des observations astronomiques ou cosmologiques, comment concilier certaines mesures avec les prévisions de la théorie (matière noire, énergie sombre).
Sommaire
- 1 Généralités
- 2 Résumé de la théorie
- 3 Conséquences de la théorie
- 4 Notes
- 5 Articles connexes
- 6 Bibliothèque virtuelle
- 7 Bibliographie
Généralités
Nécessité d'une théorie relativiste de la gravitation
La théorie de la gravitation universelle proposée par Newton à la fin du XVIIe siècle se fonde sur la notion de force de gravitation agissant selon le principe d'action à distance, c'est-à-dire le fait que la force exercée par un corps (par exemple le Soleil) sur un autre (la Terre) est déterminée par leur position relative à un instant donné, et ce quelle que soit la distance les séparant. Ce caractère instantané est incompatible avec l'idée de la relativité restreinte proposée par Einstein en 1905. En effet, selon cette dernière, aucune information ne peut se propager plus vite que la vitesse de la lumière dans le vide. Par ailleurs, le principe de l'action à distance repose sur celui de la simultanéité de deux événements : la force que le Soleil exerce sur la Terre à un instant donné est déterminée par leurs propriétés « à cet instant ». La relativité restreinte stipule que le concept de simultanéité de deux événements n'est pas défini, la perception de la simultanéité étant différente d'un observateur à un autre pour peu que ceux-ci soient animés d'une vitesse relative non nulle. Ces contradictions amènent Einstein dès 1907 à réfléchir à une théorie de la gravitation qui soit compatible avec la relativité restreinte. Le résultat de sa quête est la théorie de la relativité générale.
De la relativité de Galilée à la relativité restreinte
Au XVIe siècle, Galilée affirme et explique que les lois de la physique sont les mêmes dans des référentiels en translation rectiligne et uniforme les uns par rapport aux autres. C'est le principe de relativité (de Galilée).
Il utilisera aussi l'additivité des vitesses, selon laquelle n'importe quelle vitesse peut être atteinte, le tout n'étant qu'une question de moyens. Si une balle roule à 10 km/h dans un train (et dans le sens de la marche) qui va lui-même à 100 km/h par rapport au sol, alors la balle va à 110 km/h par rapport au sol.
Dans sa Mécanique, Isaac Newton présupposait que les corps étaient dotés d’une vitesse absolue, autrement dit qu’ils étaient soit « réellement » au repos, soit « réellement » en mouvement. Il remarqua aussi que ces vitesses absolues étaient non mesurables autrement que relativement aux vitesses des autres corps (de la même manière, la position d’un corps n’était mesurable que relativement à celle d’un autre corps, etc.). En conséquence, toutes les lois de la mécanique newtonienne devaient opérer à l’identique quel que soit le corps considéré et quel que soit son mouvement.
Cependant, Newton pensait que sa théorie ne pouvait avoir de sens sans l’existence d’un référentiel fixe absolu dans lequel la vitesse de tout corps pourrait être mesurée, même si celui-ci ne pouvait être détecté.
En fait, il est possible en pratique de bâtir une mécanique newtonienne sans cette hypothèse : la théorie résultante (nommée d’ailleurs relativité galiléenne) n’a d’ailleurs pas d’intérêt opérationnel particulier et ne doit pas être confondue avec la relativité d'Einstein qui implique en plus la constance de la vitesse de la lumière dans tous les référentiels et en moins l’hypothèse galiléenne que les vitesses relatives s’additionnent (ces deux postulats sont en effet mutuellement incompatibles).
Au XIXe siècle, le physicien écossais James Clerk Maxwell formula un ensemble d’équations, les équations du champ électromagnétique, qui conduisait à prédire la propagation d'ondes électromagnétiques de vitesse
 dans un milieu électrostatique de constante
dans un milieu électrostatique de constante  et magnétostatique de constante μ0. Cette vitesse phénoménalement élevée, même dans un milieu raréfié comme l'air, avait la même valeur que la vitesse de propagation de la lumière. Il proposa que la lumière ne soit rien d'autre qu'une onde électromagnétique.
et magnétostatique de constante μ0. Cette vitesse phénoménalement élevée, même dans un milieu raréfié comme l'air, avait la même valeur que la vitesse de propagation de la lumière. Il proposa que la lumière ne soit rien d'autre qu'une onde électromagnétique.Les théories corpusculaires de la lumière semblaient compatibles avec le principe de relativité de Galilée ainsi que la théorie de Maxwell qui penchait en faveur de l'existence d'un éther luminifère envisagé par Huygens. Mesurer la vitesse du système solaire par rapport à ce milieu élastique fut l'objet des expériences d’interférométrie menées par Michelson et Morley. Leurs expériences ont démontré que le vent apparent d'éther était nul, quelle que soit la période de l'année. Supposer que l'éther était constamment accroché à la Terre aurait été une remise en cause trop grave du principe de relativité de Galilée. D'autre part, l'éther présentait l'inconvénient d'être à la fois impalpable et très rigide puisque capable de propager les ondes à une vitesse phénoménale.
Il fallut attendre Albert Einstein en 1905 pour remettre en cause radicalement la notion d'éther, porter au plus haut le principe de relativité de Galilée en postulant que les équations de Maxwell obéissent elles-mêmes à ce principe, et en tirer les conséquences révolutionnaires dans un article resté célèbre : De l’électrodynamique des corps en mouvement.
C'est la naissance de la relativité restreinte :
- le principe de relativité de Galilée est conservé ;
- l'invariance des équations de Maxwell (par changement de référentiel inertiel) entraîne immédiatement la constance de la vitesse de la lumière c dans tous les référentiels galiléens : l'additivité des vitesses n'est plus vraie et la vitesse de la lumière est inatteignable (sauf pour la lumière, qu'elle soit considérée comme une onde ou comme constituée de photons, particules de masse nulle) ;
- les mesures de longueur, d'intervalle de temps, (et de vitesse) ne sont pas les mêmes suivant le référentiel de l'observateur : mesurer la longueur du wagon donne des résultats différents suivant que l'on est dedans ou que l'on est immobile au sol (mais ce n'est pas le cas pour la largeur du wagon, longueur perpendiculaire à la vitesse) ; de même pour l'écoulement du temps ; le champ électrique devient magnétique et réciproquement. Toutes ces transformations des systèmes de coordonnées du continuum espace-temps et du champ électromagnétique sont formalisées par les transformations de Lorentz (paradoxalement mises au point par Lorentz et Henri Poincaré pour défendre l'existence de l'éther[réf. nécessaire]) ;
- la notion de temps absolu disparaît : deux horloges identiques situées dans deux référentiels galiléens différents ne battent pas au même rythme.
En écrivant l'expression de l'énergie cinétique d'un corps de masse m de la manière la plus simple respectant le principe de relativité, Einstein a fait apparaître une énergie au repos E=mc2 qui se manifestera par la suite dans les phénomènes de fusion et de fission nucléaires.
De la relativité restreinte à la relativité générale
Article détaillé : relativité restreinte.La théorie de la relativité restreinte (1905) modifiait les équations utilisées pour comparer les mesures de longueur et de durée faites dans différents référentiels en mouvement les uns par rapport aux autres. Cela eut pour conséquence que la physique ne pouvait plus traiter le temps et l’espace séparément, mais seulement comme un espace à quatre dimensions, appelé l'espace-temps de Minkowski.
En effet, lors de mouvements à des vitesses non négligeables devant c (vitesse de la lumière dans le vide), temps et espace s'altèrent de façon liée, un peu comme deux coordonnées d'un point en géométrie analytique s'altèrent de façon liée lorsqu’on pivote les axes du repère.
Par exemple, en géométrie euclidienne habituelle la distance
 entre deux points de coordonnées
entre deux points de coordonnées  et
et  vérifie
vérifie  (avec
(avec  , etc.), mais dans l'espace de Minkowski deux points sont repérés par les coordonnées
, etc.), mais dans l'espace de Minkowski deux points sont repérés par les coordonnées  et
et  , où
, où  et
et  sont les coordonnées de temps, et la « distance », alors notée
sont les coordonnées de temps, et la « distance », alors notée  , entre ces points vérifie[4]
, entre ces points vérifie[4]  . Ce calcul donne une « distance » nulle entre deux points du parcours d'un rayon lumineux. Il donne aussi toutes les mesures de longueurs matérielles, des intervalles de temps, des vitesses en relativité restreinte, qui suscitent toujours l'étonnement.
. Ce calcul donne une « distance » nulle entre deux points du parcours d'un rayon lumineux. Il donne aussi toutes les mesures de longueurs matérielles, des intervalles de temps, des vitesses en relativité restreinte, qui suscitent toujours l'étonnement.L'espace-temps de Minkowski étant néanmoins de courbure nulle (c'est-à-dire plat) on le qualifie d'espace pseudo euclidien[5].
Tel devait être, pour Einstein, l'espace sans gravitation (et sans accélération pour l'observateur). La gravitation newtonienne, se propageant instantanément, n'est pas compatible : Einstein se mit donc en quête d'une nouvelle théorie de la gravitation.
Il admit l'égalité entre la masse gravitationnelle et la masse inertielle comme hypothèse, la fameuse formule E = mc2 autorisant alors à utiliser l'énergie totale d'un corps en lieu et place de sa masse. Ce sera fait grâce à l'outil mathématique nommé tenseur énergie.
Expert en expériences par la pensée, il imagina un disque en rotation regardé par un expérimentateur placé en son centre et tournant avec : comme pour Huygens, il y a une force centrifuge au niveau du périmètre qui est perçue comme une force gravitationnelle (car la masse gravifique et la masse inerte sont égales par hypothèse). De plus, en voulant rester dans le cadre de la relativité restreinte, il conclut que l'observateur doit constater la réduction du périmètre mais pas du rayon : ce n'est pas possible dans un espace plat. Conclusion : la gravitation oblige à utiliser une géométrie non-euclidienne.
Einstein imagina un expérimentateur enfermé dans un ascenseur aux parois opaques, subissant une montée à accélération constante : l'ascenseur d'Einstein dans lequel il est impossible pour une personne de savoir s'il y a accélération constante ou bien attraction gravitationnelle constante (car la masse gravifique et la masse inerte sont égales par hypothèse). Conclusion : équivalence locale entre mouvement accéléré et gravitation, ce qui devait se retrouver dans les équations différentielles de la nouvelle théorie. C'est son principe d'équivalence.
Enfin, Einstein voulait trouver une expression des lois de la nature (à l'époque : dynamique, gravitation et électromagnétisme) qui soit inchangée quel que soit le référentiel (accéléré ou galiléen, etc.) : c'est la relativité galiléenne généralisée à tous les repères (on nomme cela la covariance).
La grande difficulté étant de mettre ces principes sous forme mathématique, il en discuta avec David Hilbert qui, d'abord dubitatif, faillit lui ravir la vedette en trouvant la théorie en même temps que lui (voir : Controverse sur la paternité de la relativité).
La relativité générale ajouta à la relativité restreinte que la présence de matière pouvait déformer localement l’espace-temps lui-même (et non pas juste les trajectoires), de telle manière que des trajectoires dites géodésiques — c'est-à-dire intuitivement de longueur minimale — à travers l’espace-temps ont des propriétés de courbure dans l’espace et le temps. Le calcul de la « distance » dans cet espace-temps courbé est plus compliqué qu'en relativité restreinte, en fait la formule de la « distance » est créée par la formule de la courbure, et vice-versa.
Les géodésiques sont les trajectoires vérifiant le principe de moindre action, suivies par les particules test (c'est-à-dire dont l'influence sur le champ de gravitation dans lequel elles se déplacent est négligeable, ce qui est le cas par exemple d'un satellite artificiel autour de la Terre ou bien d'un photon passant à côté du Soleil mais pas d'une étoile orbitant autour d'une autre dans un système binaire oscillant rapidement), elles ont donc une importance pratique très importante pour la compréhension intuitive d'un espace courbe.
Conséquences théoriques et observations
- Einstein calcula immédiatement (1915) la déviation des positions apparentes des étoiles par le Soleil : le 29 mai 1919, les mesures furent faites par Sir Arthur Eddington lors d’une éclipse solaire, et malgré quelques imprécisions de mesure, cela constitua une première confirmation de la théorie.
- Cette théorie prévoit une rotation lente de l'ellipse de révolution de Mercure qui concorde parfaitement avec les observations.
- La gravitation (forte) d'une planète doit y contracter les longueurs observées depuis une position lointaine. Cela n'a pu être observé directement à ce jour.
- La gravitation doit ralentir le temps mesuré à distance, donc modifier les fréquences et les longueurs d'onde des rayonnements reçus et émis à distance : on peut citer par exemple une expérience menée par Pound et Rebka à l'université Harvard (1959), qui a permis de détecter un changement de la longueur d'onde d’une source monochromatique de cobalt provoqué par le champ gravitationnel terrestre sur une altitude de 22,5 mètres .
- Schwarzschild, en trouvant en 1916 une solution exacte des équations de la relativité générale en symétrie sphérique, a montré qu'il pouvait exister des conditions où un phénomène de trou noir apparaissait. L'astronomie observe des phénomènes similaires.
- Dans certaines conditions, des ondes gravitationnelles, discrètes, doivent se propager dans l'espace. L'expérience franco-italienne VIRGO cherche à en détecter.
- Autre conséquence pratique de la relativité générale : les horloges atomiques en orbite autour de la Terre du système de positionnement GPS (Global Positioning System) nécessitent une correction pour le ralentissement dû à la gravité terrestre.
Article détaillé : Tests expérimentaux de la relativité générale.Pour résumer cette théorie, Einstein amusa un public de journalistes : « Imaginez que vous regardez loin, très loin devant vous et que vous avez une très bonne vue, une très très bonne vue, alors vous arriverez à voir… votre dos ».
Résumé de la théorie
Le mouvement d'une masse d'épreuve (très petite) soumise uniquement à la gravitation des masses environnantes est en fait un mouvement inertiel dans un espace-temps courbé par ces masses (la courbure observée dépend aussi du référentiel de l'observateur). La ligne d'univers tracée dans cet espace-temps courbe est une géodésique pour une métrique obéissant aux équations non linéaires d'Einstein qui relient la courbure de l'espace-temps (vu depuis le référentiel choisi) et la présence de masses.
Référentiels et synchronisation des horloges
L’idée centrale de la relativité est que l’on ne peut pas parler de quantités telles que la vitesse ou l’accélération sans avoir auparavant choisi un cadre de référence, un référentiel. Tout mouvement, tout événement est alors décrit relativement à ce référentiel de l'observateur.
La relativité restreinte postule que ce référentiel doit être inertiel et peut être étendu indéfiniment dans l’espace et dans le temps.
Dans le but de ne privilégier aucun type de référentiels en particulier dans l'écriture des lois de la nature (principe de covariance générale), la relativité générale traite en plus les référentiels non-inertiels, c'est-à-dire dans lesquels un corps libre de toute contrainte ne suit pas un mouvement rectiligne et uniforme. Dès lors, tout système de coordonnées est a priori admissible et, généralement, ses limites se révèlent à l'usage.
En physique classique, un exemple de référentiel non-inertiel est celui d'un véhicule qui nous transporte et qui suit un virage : la force centrifuge que l’on ressent contrarie le mouvement inertiel des corps par rapport au véhicule. Un autre exemple est le référentiel lié à la terre, qui du fait de la rotation terrestre voit se manifester la force de Coriolis bien mise en valeur par le pendule de Foucault. Une force centrifuge est dite fictive car elle n'est qu'une manifestation de l'inertie (premier principe de Newton), et non pas due à l'application d'une force.
En relativité générale, il est admis que l’on ne peut définir un référentiel que localement et sur une période finie. Cette limitation est une nécessité car elle s'impose dans plusieurs cas :
- Cas le plus simple : un référentiel cartésien de l'espace en trois dimensions tournant sur lui-même autour d'un axe. L'utilisation de la relativité restreinte impose une contraction du périmètre du cercle de rotation qui aboutit à un périmètre nul à une certaine distance de l'axe de rotation. À cette distance, ce référentiel n'est plus utilisable.
- L'espace s'avérant courbe, en relativité générale, l'utilisation d'un référentiel droit (utilisé pour un espace euclidien ou pseudo-euclidien, comme l'espace de Minkowski) revient à projeter cet espace sur un espace euclidien, ce qui ne peut être que localement et provisoirement possible, de la même manière, qu'à cause de la courbure de la surface terrestre, on ne peut dessiner une carte plate sans distorsion que sur une région limitée. Un exemple célèbre est la métrique de Schwarzschild qui correspond à un référentiel sphérique pseudo-euclidien à quatre dimensions (applicable sans limitation à l'espace de Minkowski), et qui n'est plus valable à l'approche du rayon de Schwarzschild.
- La synchronisation des horloges se heurte à d'insurmontables difficultés : dans de nombreux cas il n'est pas possible de synchroniser parfaitement les horloges se trouvant sur un circuit fermé, ni même sur d'autres types d'axes de coordonnées car les propriétés de l'espace évoluant avec le système observé, des horloges initialement synchronisées se désynchronisent. On peut toutefois réussir cette synchronisation en plaçant l'observateur dans un référentiel synchrone (c'est-à-dire en chute libre dans le champ de gravitation) où sont choisis comme axes des géodésiques de l'espace-temps, évoluant au cours du temps de ce référentiel[6].
Principe d'équivalence
Article détaillé : Principe d'équivalence.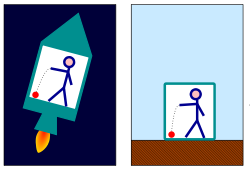 Version moderne de l'ascenseur d'Einstein : dans l'espace vide, une fusée subit une accélération constante.
Version moderne de l'ascenseur d'Einstein : dans l'espace vide, une fusée subit une accélération constante.
La chute d'un objet vue par un observateur extérieur (à gauche), et vue par l'hôte de la fusée (à droite).Parce qu’il n’a jamais été possible de mettre en évidence le moindre écart entre la masse d’inertie (résistance d’un corps à l’accélération) et la masse pesante (qui détermine son poids dans un champ de gravité), le principe d'équivalence en relativité générale postule qu’il n’y a pas lieu de distinguer localement un mouvement de chute libre dans un champ gravitationnel constant, d’un mouvement uniformément accéléré en l’absence de champ gravitationnel : dans les deux cas la chute d'un corps est décrite par la même loi, celle de la chute libre.
Ce résultat n’est que local, c’est-à-dire valable pour un espace restreint, « petit ». Dans un volume plus important et avec des accéléromètres sensibles, on distinguera au contraire très bien un champ de gravité (forces concourantes), une simple accélération (forces parallèles) et un effet centrifuge (forces divergentes). Mais dans un volume quasi-ponctuel, aucune mesure ne peut faire la distinction.
D'ailleurs, cette équivalence est utilisée dans le cadre de l’entraînement des astronautes : ceux-ci montent dans des avions effectuant un vol parabolique où la force centrifuge contrebalance quelques minutes les forces de gravité, simulant ainsi la « chute libre » d’un corps satellisé (mais dans ce cas la chute libre peut durer indéfiniment, puisque la trajectoire est une boucle).
Conséquences du principe d'équivalence
Principalement : existence d'un référentiel inertiel en chaque point de l'espace-temps, et détermination complète du champ de gravitation par la métrique du référentiel choisi.
- En chaque point de l'espace-temps il existe un référentiel localement inertiel : un référentiel en chute libre (dans le champ de gravitation, s'il y en a) dans lequel tous les corps chutent simultanément au référentiel, si bien qu'ils ne paraissent subir aucune gravitation par rapport à ce référentiel. Par hypothèse un tel référentiel décrit un espace de Minkowski, localement. Ainsi le choix d'un référentiel fait-il disparaître, localement, les effets de la gravitation, ou bien il en crée ; mais ces effets ne sont que locaux.
- En chaque point de l'espace-temps, la gravitation est décrite comme le choix d'un référentiel non-inertiel
 , et la métrique de ce référentiel contient toutes les informations sur le champ de gravitation local.
, et la métrique de ce référentiel contient toutes les informations sur le champ de gravitation local.
Construction de la métrique. Si sont les coordonnées dans un référentiel inertiel local (avec, par convention,
sont les coordonnées dans un référentiel inertiel local (avec, par convention,  ), la métrique de cet espace de Minkowski est notée
), la métrique de cet espace de Minkowski est notée  , avec la convention d'Einstein, et comme
, avec la convention d'Einstein, et comme  , on obtient comme métrique pour le référentiel non-inertiel choisi :
, on obtient comme métrique pour le référentiel non-inertiel choisi :  , que l'on note aussi
, que l'on note aussi  , avec
, avec  .
.
Construction du référentiel. La métrique étant donnée, la recherche des
étant donnée, la recherche des  ne donne pas une solution unique, mais donne une infinité de solutions correspondantes, pour la moitié d'entre elles[7], à un changement de référentiel non-inertiel
ne donne pas une solution unique, mais donne une infinité de solutions correspondantes, pour la moitié d'entre elles[7], à un changement de référentiel non-inertiel  à
à  inertiel ; et pour chacune de ces solutions, en connaissant un des deux référentiels on obtient l'autre par intégration.
inertiel ; et pour chacune de ces solutions, en connaissant un des deux référentiels on obtient l'autre par intégration.
Le temps propre
 du référentiel inertiel (Minkowskien) vérifie
du référentiel inertiel (Minkowskien) vérifie  . En posant
. En posant  , avec la convention d'Einstein, on peut écrire
, avec la convention d'Einstein, on peut écrire  .
.La matrice
 est inversible, comme tout changement de référentiel est mathématiquement réversible.
est inversible, comme tout changement de référentiel est mathématiquement réversible.Dérivée covariante
Article détaillé : Dérivée covariante.Cas général
Soit un quadrivecteur
 pour un référentiel (localement) inertiel
pour un référentiel (localement) inertiel  . Ses coordonnées dans un référentiel quelconque
. Ses coordonnées dans un référentiel quelconque  sont
sont  , avec
, avec  .
.On a donc
 .
.On nomme « symboles de Christoffel » les termes
 et
et  , qui souvent s'expriment par une formule différente mais équivalente[8].
, qui souvent s'expriment par une formule différente mais équivalente[8].En appelant différentielle absolue ou différentielle covariante l'opérateur
 ou
ou  défini par
défini par  , on peut écrire
, on peut écrire  .
.On a donc la propriété :
 .
.On appelle parfois principe de correspondance en relativité générale le fait de pouvoir substituer
 à
à  dans les équations de la physique classique pour en faire des équations de la physique relativiste, dans la mesure où des quadrivecteurs peuvent y remplacer les vecteurs[8].
dans les équations de la physique classique pour en faire des équations de la physique relativiste, dans la mesure où des quadrivecteurs peuvent y remplacer les vecteurs[8].La dérivée covariante du quadri-vecteur dans le référentiel quelconque est définie par

Dans le cas où, par rapport au référentiel inertiel, le quadri-vecteur est constant au cours du temps propre
 , on a
, on a  .
.Particule en chute libre
Considérons une particule de masse non-nulle mais négligeable (c'est-à-dire n'influençant pas le champ gravitationnel environnant de manière significative) en chute libre : un référentiel associé à cette particule est donc inertiel et dedans sa quadri-vitesse, de coordonnées
 , y est constante.
, y est constante.On obtient donc dans un référentiel quelconque
 et
et  .
.Cette équation peut aussi s'écrire
 , ce que l'on nomme aussi équation des géodésiques en relativité générale.
, ce que l'on nomme aussi équation des géodésiques en relativité générale.Par ailleurs, pour toute particule en chute libre, on a
 , donc
, donc  : la pseudo-norme de la quadri-vitesse est égale à c dans tout référentiel.
: la pseudo-norme de la quadri-vitesse est égale à c dans tout référentiel.Ces calculs n'ont pas lieu d'être pour une particule de masse nulle car son temps propre n'existe pas.
Particule de masse nulle
Dans le cas d'une particule de masse nulle, dont on suppose qu'elle n'influence pas le champ de gravitation environnant, on ne peut utiliser son temps propre car il n'existe pas, par contre on sait que dans un référentiel inertiel, sa vitesse est constante, donc
 d'où
d'où  .
.On en tire
 [9]. Cette égalité est d'ailleurs aussi vérifiée par les particules massives (toujours de masse négligeable) en chute libre.
[9]. Cette égalité est d'ailleurs aussi vérifiée par les particules massives (toujours de masse négligeable) en chute libre.Par ailleurs, la pseudo-norme de la quadri-vitesse des particules de masse nulle est
 dans tout référentiel.
dans tout référentiel.Si la lumière est bien modélisée par des particules de masse nulle, elle subit bien la gravitation en relativité générale, suivant une même loi que les autres particules ; seules changent les coordonnées de la vitesse initiale.
Dynamique
Supposons que dans un référentiel quelconque soit exercée une force relativiste, sous la forme d'un quadri-vecteur
 , sur le corps observé. Par changement de référentiel, on peut considérer cette force dans un référentiel d'inertie local par un quadri-vecteur
, sur le corps observé. Par changement de référentiel, on peut considérer cette force dans un référentiel d'inertie local par un quadri-vecteur  tel que
tel que  .
.De l'égalité
 , en physique classique, on tire par le principe de correspondance
, en physique classique, on tire par le principe de correspondance  en relativité restreinte, puis enfin
en relativité restreinte, puis enfin  , équation de la dynamique relativiste en présence d'un champ de gravitation.
, équation de la dynamique relativiste en présence d'un champ de gravitation.Tenseur d’énergie et courbure de l’espace
Mathématiquement parlant, Einstein modélise l’espace-temps par une variété pseudo-riemannienne quadri-dimensionnelle, et son équation du champ gravitationnel relie la courbure de la variété en un point, au tenseur énergie-impulsion en ce point, ce tenseur étant une mesure de la densité de matière et d’énergie (étant entendu que matière et énergie sont équivalentes).
Cette équation est à la base de la fameuse formule qui dit que la courbure de l’espace définit le mouvement de la matière, et la matière définit la courbure de l’espace (les deux étant équivalents). La meilleure façon de se représenter la géométrie de l’espace-temps est d’imaginer que celui-ci se comporte comme une surface élastique creusée localement par la présence d’un objet massif, une boule par exemple. Pour reprendre une expression célèbre due à John Archibald Wheeler : « La masse et l’énergie disent à l’espace-temps comment se courber, et la courbure de l’espace-temps dit à la matière comment se comporter ».
Tenseur d'énergie
Article détaillé : Tenseur énergie-impulsion.Le tenseur d'énergie-impulsion
 est le tenseur de densité de l'énergie et de l'impulsion de la matière répartie dans l'espace. Il généralise le quadrivecteur énergie-impulsion de la relativité restreinte : cela est rendu nécessaire par l'étude de la matière comme étendue dans l'espace.
est le tenseur de densité de l'énergie et de l'impulsion de la matière répartie dans l'espace. Il généralise le quadrivecteur énergie-impulsion de la relativité restreinte : cela est rendu nécessaire par l'étude de la matière comme étendue dans l'espace.En posant
 , on montre que ce tenseur vérifie
, on montre que ce tenseur vérifie  .
.Courbure de l'espace-temps
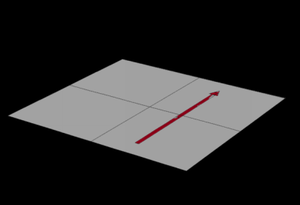
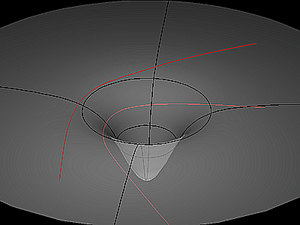
Article détaillé : Tenseur d'Einstein. Situation visible : sur une sphère. Le vecteur tangent noir est transporté par deux chemins différents le long de géodésiques : un chemin bleu et un rouge. À l'arrivée, l'orientation du vecteur obtenu dépend du chemin : cette différence, qui n'existe pas (est nulle) en géométrie plane, est mesurée par le tenseur de Riemann-Christoffel.
Situation visible : sur une sphère. Le vecteur tangent noir est transporté par deux chemins différents le long de géodésiques : un chemin bleu et un rouge. À l'arrivée, l'orientation du vecteur obtenu dépend du chemin : cette différence, qui n'existe pas (est nulle) en géométrie plane, est mesurée par le tenseur de Riemann-Christoffel.
Dans un espace plat (euclidien ou pseudo-euclidien comme celui de Minkowski), le théorème de Schwarz dit que
 , ce que l'on écrit aussi
, ce que l'on écrit aussi ![\left[ \partial^i ; \partial^j \right] = 0](3/cb3afd782efbda2b1bd926e53e21aa44.png) , avec
, avec  et
et ![\ [A;B]= A \circ B - B \circ A](d/2fd09bfbf810f41003d62e94edfd5f7e.png) .
.Une mesure de la courbure de l'espace est dans l'expression de
![\left[ \nabla^i ; \nabla^j \right] = \frac{\nabla~}{\partial x_i}\frac{\nabla~}{\partial x_j} - \frac{\nabla~}{\partial x_j}\frac{\nabla~}{\partial x_i}](2/51235d9241eb250e8d7156e107133863.png) , avec
, avec  . Émerge de ces calculs un peu laborieux le tenseur de Riemann-Christoffel construit uniquement à partir de la métrique
. Émerge de ces calculs un peu laborieux le tenseur de Riemann-Christoffel construit uniquement à partir de la métrique  .
.Quelques calculs supplémentaires permettent d'en tirer le tenseur de Ricci
 . Ce tenseur vérifie un certain nombre de propriétés qui le rendent incontournable dans la recherche du lien entre la courbure de l'espace et les corps qui y sont présents. On défini aussi le scalaire nommé la courbure principale
. Ce tenseur vérifie un certain nombre de propriétés qui le rendent incontournable dans la recherche du lien entre la courbure de l'espace et les corps qui y sont présents. On défini aussi le scalaire nommé la courbure principale  .
.Einstein savait que le tenseur
 vérifie l'égalité
vérifie l'égalité  , comme le tenseur énergie-impulsion.
, comme le tenseur énergie-impulsion.Élie Cartan montra, après qu'Einstein eut exposé ses équations de la relativité générale, que le seul tenseur
 non trivial, d'ordre 2, lié à la géométrie et vérifiant cette dernière égalité est bien ce tenseur, nommé maintenant le « tenseur d'Einstein ».
non trivial, d'ordre 2, lié à la géométrie et vérifiant cette dernière égalité est bien ce tenseur, nommé maintenant le « tenseur d'Einstein ».Les équations d'Einstein
Article détaillé : Équation d'Einstein.Einstein a postulé que les équations liant la matière présente et la courbure de l'espace sont
 où
où  est une constante homogénéisant les dimensions. On détermine par l'approximation newtonienne que
est une constante homogénéisant les dimensions. On détermine par l'approximation newtonienne que  .
.Hilbert a justifié cette équation par le principe de moindre action dès 1915[10].
Dans ces équations, il s'agit de prolonger le lien créé entre la masse inertielle et l'énergie totale du corps, énoncé dans relativité restreinte, en une relation reliant la cause de la gravitation (la courbure de l'espace) à l'énergie de la matière présente.
L’équation du champ d’Einstein n’est pas linéaire, et n'a pas une solution unique. Pour la relativité générale, les lois de Newton ne sont que des approximations valables dans un référentiel local, à faible champ de gravitation et pour de petites vitesses.
La relativité générale se distingue des autres théories existantes par la simplicité du couplage entre matière et courbure géométrique, mais il reste à réaliser l’unification entre la relativité générale et la mécanique quantique, et le remplacement de l’équation du champ gravitationnel par une loi quantique plus générale. Peu de physiciens doutent qu’une telle Théorie du Tout donnerait lieu aux équations de la relativité générale dans certaines limites d’application, de la même manière que cette dernière permet de redonner la loi de la gravitation de Newton comme approximation.
Constante cosmologique et observations
L’équation du champ peut contenir un paramètre « supplémentaire » appelé la constante cosmologique
 qui a été introduite à l’origine par Einstein pour qu’un univers statique (c’est-à-dire un univers qui n’est ni en expansion, ni en contraction) soit solution de son équation.
qui a été introduite à l’origine par Einstein pour qu’un univers statique (c’est-à-dire un univers qui n’est ni en expansion, ni en contraction) soit solution de son équation.Les équations d'Einstein s'écrivent alors :
 .
.Cet effort se solda par un échec pour deux raisons : d'un point de vue théorique, l’univers statique décrit par cette théorie est instable ; et de plus les observations de l’astronome Edwin Hubble dix ans plus tard démontrèrent que l’Univers était en fait en expansion. Donc
 fut abandonnée, mais récemment, des techniques astronomiques ont montré qu’une valeur non nulle de ce paramètre est nécessaire pour expliquer certaines observations.
fut abandonnée, mais récemment, des techniques astronomiques ont montré qu’une valeur non nulle de ce paramètre est nécessaire pour expliquer certaines observations.L’étude des solutions de l'équation d'Einstein est une branche de la physique nommée cosmologie. Elle permet notamment d’expliquer l’excès de l’avance du périhélie de Mercure, de prédire l’existence des trous noirs, des ondes gravitationnelles et d’étudier les différents scénarii d’évolution de l’Univers. Notons que l’astrophysicien bien connu Stephen Hawking a démontré qu’un univers comme le nôtre comportait nécessairement des singularités gravitationnelles.
Plus récemment (octobre 2004), des mesures effectuées par laser avec les satellites LAGEOS ont montré que le champ gravitationnel de la Terre lui-même engendre des distorsions de positionnement de la Lune de deux mètres par an[11] comparativement à ce qui serait prévu par les seules lois de Newton. Ce chiffre est en accord à 1% près avec ce qui est prévu par la Relativité générale.
Conséquences de la théorie
Lentille gravitationnelle
Article détaillé : Lentille gravitationnelle.La lumière suit les géodésiques (des lignes d'espace-temps) qui sont déformées aux abords d'un corps massif par effet de la gravitation. Par conséquent, et contrairement aux prévisions newtonniennes, la trajectoire de la lumière peut être fortement infléchie en présence d'un corps massif (une planète particulièrement massive) près de la trajectoire d'un rayon, et même deux rayons issus d'un même corps présent d'un côté de la planète massive, et dirigés dans des directions différentes, peuvent se rejoindre du côté opposé et créer une image dédoublée, une sorte de mirage d'origine gravitationnelle.
De tels phénomènes sont observés depuis de nombreuses années et pourraient servir à la détection de la matière noire présente dans l'univers.
Trou noir
Article détaillé : Trou noir.À la suite de la découverte de la métrique de Schwarzschild (1916), il est apparu dans les équations que pour toute masse sphérique il existe une distance au centre (le rayon de Schwarzschild) où des phénomènes particuliers se manifestent, si la masse est de rayon inférieur : pour un observateur un peu éloigné, les corps s'approchant de ce rayon semblent s'immobiliser, ses horloges s'arrêter et ceci pour l'éternité ; de plus, mis à part les phénomènes gravitationnels, nulle information ne semble pouvoir venir de cette masse centrale, pas même la lumière, et la masse centrale elle-même n'est décelable que par ses effets gravitationnels.
Toutefois, ce rayon de Schwarzschild n'apparut que comme une possible singularité topologique de l'espace-temps, une absurdité qui marquait une limite de la théorie, ce qui ne satisfaisait pas Einstein. Entre 1938 (Georges Lemaître) et 1939 (Robert Oppenheimer) est émise l'hypothèse que c'était un phénomène réaliste, nommé collapse gravitationnel[12]. Dans les années 1960, la nature de ce phénomène a été précisée : il a été compris que le rayon de Schwarzschild n'est pas une singularité topologique de l'espace-temps mais seulement une singularité de la métrique utilisée due à la courbure de l'espace alors que la métrique est construite comme si l'espace était plat. Les phénomènes décrits par la métrique de Schwarzschild restent valables pour l'observateur éloigné, une métrique de Kruskal (1960) a permis de comprendre comment se fait le passage du rayon de Schwarzschild pour le voyageur[12].
Depuis, différents types de trous noirs ont été mis en évidence (avec ou sans charge ou moment cinétique), leur dynamique a été étudiée en détails, l'hypothèse de leur évaporation a été précisément formulée, et la notion, très hypothétique, de trou de ver a été avancée. L'observation et la détection des trous noirs est toujours l'objet de travaux intenses.
Ondes gravitationnelles
Article détaillé : Onde gravitationnelle.En considérant un champ de gravitation faible, la métrique
 s'écarte peu de la métrique
s'écarte peu de la métrique  de l'espace de Minkowski :
de l'espace de Minkowski :  . Avec la condition de petitesse de
. Avec la condition de petitesse de  et en ajoutant une condition de jauge[13], le tenseur de Ricci peut prendre la forme simple
et en ajoutant une condition de jauge[13], le tenseur de Ricci peut prendre la forme simple  , où
, où  est le d'alembertien.
est le d'alembertien.Dans le vide, l'équation d'Einstein s'écrit
 , ce qui est une équation d'onde. La gravitation peut donc, dans ces conditions, être considérée comme une onde.
, ce qui est une équation d'onde. La gravitation peut donc, dans ces conditions, être considérée comme une onde.On peut de même considérer la gravitation comme une perturbation ondulatoire par rapport à une métrique quelconque non-perturbée, c'est-à-dire dans un espace-temps courbe, et on peut aussi considérer des ondes gravitationnelles de forte intensité, et étudier le rayonnement énergétique de ces ondes (en utilisant le tenseur énergie-impulsion)[14].
La détection de telles ondes est l'objet d'intenses recherches internationales, cependant, la petitesse des énergies mises en jeu les rend difficilement perceptibles. Les seules détections faites à ce jour sont indirectes : en 1974, une perte d'énergie a été observée dans un pulsar binaire (PSR 1913+16) et a été interprétée comme due à l'émission d'ondes gravitationnelles ; par la suite, de nombreuses observations plus précises n'ont fait que confirmer le modèle théorique ; on trouvera un exposé plus détaillé de ces observations dans la section correspondante de l'article Pulsar binaire.
La physique quantique permet d'émettre l'hypothèse qu'à cette onde est associée une particule responsable de l'interaction gravitationnelle : le graviton, de masse nulle car se déplaçant à la vitesse de la lumière dans le vide.
Modèles d'Univers
Article détaillé : Modèle cosmologique.L'hypothèse de l'homogénéité et l'isotropie, qui constitue le principe cosmologique et qui est en accord avec les observations sur une grande échelle, implique que l'on peut choisir un temps universel tel que la métrique de l'espace soit la même à tout instant, pour tous les points et dans toutes les directions[15], ce qui est compatible avec la théorie du Big Bang qui prévaut actuellement.
À partir des équations d'Einstein, plusieurs modèles d'Univers sont possibles. En 1915, Einstein concevait l'Univers comme stationnaire, ce que les observations cosmologiques ont contredit. Plus tard Alexandre Friedmann et Georges Lemaître ont proposé des modèles non-stationnaires : la métrique de Friedmann-Lemaître-Robertson-Walker montre que trois modèles homogènes et isotropes de l'Univers sont possibles suivant la valeur d'un paramètre dans la métrique : espace plat (en moyenne), à courbure positive (univers dit fermé : de volume fini), ou à courbure négative (univers dit ouvert : de volume infini). D'autres modèles cosmologiques, plus exotiques, sont compatibles avec les équations de la relativité générale. Par exemples : l'Univers de de Sitter correspondant en physique un univers homogène, isotrope, vide de matière et ayant une constante cosmologique positive ; l'univers mixmaster qui est un univers vide de matière, homogène mais anisotrope, dont le taux d'expansion diffère dans les trois directions d'espace ; l'Univers de Gödel qui ne respecte pas le principe de causalité.
Notes
- Suivant le référentiel de l'observateur, l'énergie cinétique d'un corps peut être nulle, très importante, constante, variable, etc : ces différences se retrouvent dans les différences de courbures de l'espace-temps, courbure due à ce corps, telle qu'elles sont constatées par les différents observateurs depuis leur référentiel respectif, et donc elles se retrouvent dans les différences entre les effets gravitationnels mesurés par les différents observateurs.
- À l'exception possible de l'anomalie Pioneer qui pourrait être la première indication d'un écart entre les phénomènes observés et la relativité générale, quoique d'autres interprétations de ce phénomène soient envisageables
- Ainsi, une théorie cohérente unifiant relativité générale et physique quantique permettrait peut-être d'apporter des réponses au problème de la platitude de l'univers.
- La pseudo-métrique, notée
 , est définie par
, est définie par  ou
ou  suivant la convention de signes ( − ; + ; + ; + ) ou
suivant la convention de signes ( − ; + ; + ; + ) ou  choisie ; la convention
choisie ; la convention  , utilisée ici, correspond au choix fait dans les textes anglo-saxons ; la convention
, utilisée ici, correspond au choix fait dans les textes anglo-saxons ; la convention  correspond au choix fait dans les célèbres textes pédagogiques de Lev Landau, par exemple. Ce dernier choix est considéré comme « plus physique » par Roger Penrose car la métrique est positive pour les lignes d'univers de genre temps, qui sont les seules admises pour des particules massives. Au signe près, cette définition rend la pseudo-métrique identique à l'intervalle d'espace-temps qui est l'invariant relativiste par changement de référentiel galiléen.
correspond au choix fait dans les célèbres textes pédagogiques de Lev Landau, par exemple. Ce dernier choix est considéré comme « plus physique » par Roger Penrose car la métrique est positive pour les lignes d'univers de genre temps, qui sont les seules admises pour des particules massives. Au signe près, cette définition rend la pseudo-métrique identique à l'intervalle d'espace-temps qui est l'invariant relativiste par changement de référentiel galiléen. - Wolfgang Pauli ; Theory of relativity, Dover Publications, Inc. (1981), ISBN 0-486-64152-X (page 62).
- Lev Landau et Evguéni Lifchitz, Physique théorique, tome 2 : Théorie des champs, éd. MIR, Moscou [détail des éditions], §84 et §97.
- Parmi les changements de référentiels mathématiques, il convient d'écarter ceux qui changent l'orientation du temps ou de l'espace (règle de la main droite) et qui ne sont donc pas physiquement réalistes.
- Edgard Elbaz, Relativité générale et gravitation, édition ellipse, 1986, (ISBN 2729886516)
- Ce résultat ne vient pas d'une simple division car l'écriture
 contient des sommations d'indices que l'utilisation de la convention d'Einstein peut faire oublier.
contient des sommations d'indices que l'utilisation de la convention d'Einstein peut faire oublier. - Jean-Claude Boudenot date à 1916, page 162 de son livre Électromagnétisme et gravitation relativistes, ellipse (1989), ISBN 2-7298-8936-1; dans Lev Landau et Evguéni Lifchitz, Physique théorique, tome 2 : Théorie des champs, éd. MIR, Moscou [détail des éditions], §93 note en bas de page du début de paragraphe, il est dit que cette méthode a été suggérée par Hilbert dès 1915, ce que confirme Jean-Paul Auffray p247 (paragraphe Hilbert part à la pêche) de son livre Einstein et Poincaré, édition Le Pommier, 1999, ISBN 2 746 50015 9.
- Access : Spinning Earth twists space : Nature News
- Lev Landau et Evguéni Lifchitz, Physique théorique, tome 2 : Théorie des champs, éd. MIR, Moscou [détail des éditions], §102 à §104.
- Lev Landau et Evguéni Lifchitz, Physique théorique, tome 2 : Théorie des champs, éd. MIR, Moscou [détail des éditions], §107.
- Lev Landau et Evguéni Lifchitz, Physique théorique, tome 2 : Théorie des champs, éd. MIR, Moscou [détail des éditions], §108 à §110.
- Lev Landau et Evguéni Lifchitz, Physique théorique, tome 2 : Théorie des champs, éd. MIR, Moscou [détail des éditions], §111.
Articles connexes
Théories
Tests et observations
Mathématiques
- Action d'Einstein-Hilbert
- Courbure
- Covariance
- Géométrie dans l'espace
- Géométrie différentielle
- Géométrie non euclidienne
- Ligne d'univers
- Paramétrisation post-newtonienne
- Variété riemannienne
- Variété lorentzienne
Astronomie
Bibliothèque virtuelle
Cours en ligne
- Laurent Baulieu ; Introduction à la relativité générale, cours d'introduction donné à l'École polytechnique par un chercheur du Laboratoire de physique théorique des hautes énergies de l'université Paris 6 (Fichier pdf — 53 pages.)
- Éric Gourgoulhon : Relativité générale, cours de Master 2e année, Observatoire de Paris et Universités Paris 6, Paris 7 et Paris 11 (fichier PDF — 188 pages)
- (en) Sean M. Carroll ; Lecture notes on general relativity, cours approfondi donné en 1997 par un membre de l'Institute for Theoretical Physics, University of California at Santa Barbara (USA) (Fichiers Postscript et pdf — 238 pages)
- (en) General Relativity Trimester, série de cours approfondis donnés en 2006 à l'Institut Henri Poincaré (Paris).
Lectures complémentaires
- Living Reviews in Relativity : les articles en ligne publiés sur ce site, géré par l'Institut Max-Planck pour la Gravitation de Potsdam (RFA), sont régulièrement remis à jour par leurs auteurs, tous spécialistes de leur domaine de contribution.
- John C. Baez & Emory F. Bunn ; The meaning of Einstein's equations, American Journal of Physics 73 (2005), 644-652. Remarquable article pédagogique écrit en 2001 par un membre du Department of Mathematics, University of California at Riverside (USA). Donne une interprétation géométrique simple des équations du champ d'Einstein. Une version plus complète est disponible sur l'ArXiv : gr-qc/0103044
- Lee C. Loveridge ; Physical & geometric interpretations of the Riemann tensor, Ricci tensor & scalar curvature, remarquable article pédagogique écrit en 2004. (18 pages)
- Clifford M. Will ; Was Einstein Right? Testing Relativity at the Centenary, un article de revue écrit en 2005 par le spécialiste américain des tests expérimentaux de la relativité. (21 pages.) Publié dans : 100 Years of Relativity : Spacetime Structure — Einstein and Beyond, ed. Abhay Ashtekar (World Scientific, Singapour).
- R. Arnowitt, Stanley Deser et Charles W. Misner ; The dynamics of general relativity, un article écrit en 1962 sur la formulation canonique Hamiltonienne de la relativité générale, formulation passée à la postérité sous le nom de « formulation ADM ». (30 pages.)
- Robert Bartnik & Jim Isenberg ; The constraint equations, un article de revue écrit en 2004 sur le problème de Cauchy en relativité générale. À paraître dans : P.T.Chrusciel and H. Friedrich (eds.) ; 50 Years of the Cauchy Problem, in honour of Yvonne Choquet-Bruhat, proceedings of the 2002 Cargese meeting (34 pages.)
- Joel M. Weisberg & Joseph H. Taylor ; Relativistic binary puslar B1913+16 : thirty years of observations & analysis, un article de synthèse écrit en 2004 sur les mesures effectuées sur le pulsar binaire découvert en 1974 par Russel Hulse & Joseph Taylor, prix Nobel 1993. (7 pages.)
- Thomas B. Bahder ; Clock synchronisation & navigation in the vincinity of the Earth, un article de revue écrit en 2004 sur le problème de la « synchronisation des horloges » en relativité générale, avec application au GPS. (49 pages.)
- Norbert Straumann ; The history of the cosmological constant problem, un article de revue sur la constante cosmologique écrit en 2002 par un membre du Département de physique théorique de l'université de Zurich (Suisse). (12 pages.)
- Norbert Straumann ; On the Cosmological Constant Problems and the Astronomical Evidence for a Homogeneous Energy Density with Negative Pressure, un article de revue sur la constante cosmologique et l'énergie du vide écrit en 2002 pour le premier séminaire Poincaré. (51 pages.)
- Norbert Straumann ; Dark Energy, un article de revue sur l'énergie du vide écrit en 2003. (16 pages.)
- Y. Verbin & N.K. Nielsen ; On the origin of Kaluza's idea of unification, un court article écrit en 2004 sur l'origine de la théorie de Kaluza-Klein. Publié dans : General Relativity and Gravitation 37 (2005) 427-433 (5 pages.)
- Jacob D. Beckenstein ; Black holes : physics & astrophysics, un article de synthèse sur les trous noirs, écrit par un spécialiste en 2004. D'après des cours donnés au NATO advanced study institute Neutrinos and explosive events in the universe, Erice (2-13 juillet 2004) (26 pages.)
- E.G. Adelberger, B.R. Heckel, A.E. Nelson ; Tests of the Gravitational Inverse-Square Law, un article de revue écrit par des membres de l'université de Washington, Seattle (USA) publié dans : Annual Review of Nuclear and Particle Science 53 (2003) 77-121.
Divers
- (fr) Relativité générale : comment l'espace-temps devint dynamique, Futura-Sciences
- (fr) Les aventures d’Anselme Lanturlu Le géométricon et Tout est relatif, bandes dessinées de Jean-Pierre Petit, éd. Belin,
- (fr) Miettes de relativité générale, introduction très inspirée du cours en ligne donné par Léonard Süskind à Stanford
- (fr) Cours de relativité générale - CNRS, Observatoire de Paris, Université Paris Diderot
Bibliographie
Vulgarisation
- Albert Einstein ; La relativité, Gauthier-Villars (1956). Réédité par Payot (1990) (ISBN 2228882542). Au format poche, un exposé élémentaire des principes de la théorie de la relativité restreinte et générale, par son auteur. Indémodable.
- Gianni Pascoli ; La gravitation, Ed PUF, Collection Que sais-je ?. Exposé court des problématiques qui ont amené la relativité générale, et études de quelques conséquences de cette théorie.
- Banesh Hoffmann ; Histoire d'une grande idée : la relativité, Éditions Pour La Science (1985), diffusion Belin (ISBN 2-9029-1844-5). Un exposé remarquable pour sa clarté et sa simplicité de la relativité, par un ancien collaborateur d'Einstein à l'Institute for Advanced Studies de Princeton.
- Thibault Damour ; Si Einstein m'était conté, Éditions du Cherche-midi, Paris (2005) (ISBN 2-74910-390-8). Le grand spécialiste français des théories de la relativité nous livre enfin « son » Einstein sans équations. Thibault Damour est professeur permanent à l'Institut des Hautes Études Scientifiques (IHES) de Bures-sur-Yvette ; il a longtemps enseigné la relativité générale au DEA de physique théorique de la rue d'Ulm.
- Clifford M. Will ; Les enfants d'Einstein — La relativité générale à l'épreuve de l'observation, InterEditions (Paris-1988), (ISBN 2-7296-0228-3). Quelques-uns des résultats expérimentaux — parfois récents — qui confirment tous la théorie d'Einstein, par un expert.
- Albert Einstein & Leopold Infeld ; L'évolution des idées en physique, Collection Champs, Flammarion (1993) (ISBN 2080811193). Au format poche, une histoire de la physique, de la Mécanique de Newton jusqu'aux théories modernes (relativité, quanta), écrite en 1936 par le Maître lui-même et l'un de ses disciples à Princeton, pour financer le séjour de ce dernier. Accessible dès la terminale scientifique, un ouvrage qui invite à la réflexion et qui fait aimer une physique vivante et accessible.
- Jean-Pierre Luminet ; Les trous noirs, Collection Points-Sciences, Le Seuil (1992), (ISBN 2020159481). Un ouvrage au format poche, par un expert français de l'Observatoire de Meudon travaillant sur le sujet. Introduit l'éventuelle possibilité de voyager dans le temps au moyen de trous de ver.
- Kip S. Thorne ; Trous noirs & distorsions du temps — L'héritage sulfureux d'Einstein, Nouvelle Bibliothèque Scientifique, Flammarion (1997). Réédité dans la collection Champs (2001), (ISBN 208081463X). Un livre essentiellement consacré aux trous noirs, par un spécialiste du genre, professeur de Physique Théorique au Californian Institute of Technology. Le dernier chapitre présente les recherches les plus récentes (et spéculatives) de l'auteur sur les voyages dans le temps.
- Stephen Hawking ; Une brève histoire du temps — Du Big-Bang aux trous noirs, Flammarion (1989). Réédité par J'ai lu (2000), (ISBN 2290307114). Un ouvrage d'initiation à la cosmologie moderne, par un physicien théoricien anglais célèbre de l'Université de Cambridge. La première partie du livre est un exposé de la théorie classique du Big-Bang. La seconde partie présente les résultats plus récents de l'auteur concernant la cosmologie quantique ; plus difficile à lire pour le profane, cette partie est également beaucoup plus spéculative : l'approche d'Hawking constitue une théorie parmi d'autres, non encore confirmée par l'expérience.
- Thibault Damour ; Le renouveau de la relativité générale, La Recherche 189 (Juin 1987) 766-776. Un article qui expose simplement la théorie et ses développements récents (trous noirs, ondes gravitationnelles…).
- (en) John A. Wheeler ; A journey into gravity & space-time, Freeman & Co. (1999), (ISBN 0-7167-6034-7). La relativité générale vulgarisée par un expert mondial.
- (en) Robert Geroch ; General relativity — From A to B, the University of Chicago Press (1978), (ISBN 0-226-28864-1). Une introduction non mathématique à la relativité générale, issue d'un cours donné à des non-scientifiques, par un professeur de physique mathématique de l'Université de Chicago.
- (en) Bernard Schutz ; Gravity from the ground up — An introductory guide to gravity & general relativity, Cambridge University Press (2003), (ISBN 0-521-45506-5). Superbe introduction aux phénomènes gravitationnels.
- (en) Herman Bondi : Relativity and Common Sense, Heinemann (1964), ISBN . Une introduction accessible à tous par un scientifique renommé.
Ouvrages d'initiation
Accessibles au niveau du premier cycle universitaire.
- Dennis Sciama ; The Physical Foundations of General Relativity, Doubleday (1969), ISBN 0-385-02199-2. Né en 1926 en Angleterre, l'auteur est un astrophysicien qui a été dès la fin des années 1950 l’un des grands théoriciens des trous noirs. Il a joué un rôle déterminant en impulsant les recherches dans ce domaine ; il a notamment eu Stephen Hawking et Martin Rees comme étudiants à l'université de Cambridge. Il a existé autrefois une traduction française de cet excellent livre : Les bases physiques de la relativité générale, Dunod (1971), hélas non rééditée.
- E.F. Taylor & John A. Wheeler ; À la découverte de l'espace-temps, Dunod (1970). Cet ouvrage original est une introduction élémentaire, quoique rigoureuse, à la théorie de la relativité restreinte ; Wheeler est un expert incontesté du domaine. Le public visé est l'étudiant de premier cycle débutant en physique ; en particulier, la connaissance de l'électromagnétisme n'est pas nécessaire. C'est le complément idéal pour prolonger la lecture du livre de Banesh Hoffman cité ci-dessus. De nombreux exercices, dont une bonne part résolus. Malheureusement plus édité en français, cet ouvrage reste disponible en anglais : Spacetime Physics, W. H. Freeman (2e édition — 1992), ISBN 0-7167-2327-1.
- Jean-Marc Levy-Leblond ; Les relativités, Cahiers de Fontenay n 8, École normale supérieure de Fontenay-aux-Roses (1977). Notes de cours très pédagogiques, hélas non publiées. Se trouve dans toute bonne bibliothèque universitaire.
- Thibault Damour & Stanley Deser ; Relativité, Encyclopeadia Universalis 19 (1995) 739-748. Un exposé non technique d'une grande clarté, par un spécialiste de notoriété mondiale : Thibault Damour est professeur permanent à l'Institut des Hautes Études Scientifiques (IHES) de Bures-sur-Yvette ; il a longtemps enseigné la relativité générale au DEA de physique théorique de la rue d'Ulm.
- Jean-Pierre Provost & Marie-Antoinette Tonnelat ; Espace-temps, Encyclopeadia Universalis 8 (1995) 743-745. Un exposé d'introduction assez simple, ou l'essentiel de la relativité en quatre pages.
- Max Born ; La théorie de la relativité d'Einstein et ses bases physiques, Gauthier-Villars (1923). Réédité par Jacques Gabay (2003) ISBN 2-87647-230-9. Cet ouvrage, écrit par un grand théoricien allemand, prix Nobel 1954, est remarquable pour sa clarté. La place occupée par l'aspect mathématique y est extrêmement réduite.
- Wolfgang Rindler ; Relativity : special, general and cosmological, Oxford University Press (3e édition-2001), ISBN 0-19-850836-0. Une introduction brillante à tous les aspects de la relativité, par un professeur de l'Université de Dallas (Texas), spécialiste du domaine.
- Wolfgang Rindler ; Essential relativity : special, general and cosmological, Texts and Monographs in Physics, Springer-Verlag (2e édition révisée-1977), ISBN 3-540-10090-3. Édition antérieure du livre précédent, toujours intéressante.
- George F.R. Ellis & Ruth M. Williams ; Flat & curved space-times, Oxford University Press (2e édition-2000), ISBN 0-19-850656-2. Une autre excellente introduction à la relativité, par un expert, professeur de l'Université de Cape-Town (Afrique du Sud), et sa collaboratrice.
- Arthur S. Eddington ; Space, time & gravitation — An outline of the general relativity theory, Cambridge Science Classics Series, Cambridge University Press (1987), ISBN 0-521-33709-7. Réédition d'un classique, paru originellement en 1920, par le grand astronome Anglais qui vérifia pour la première fois l'une des prédictions théoriques de la relativité générale : la déviation de la lumière par un corps massif, observée en 1919 lors d'une éclipse totale du Soleil. (Il a existé autrefois une traduction française de cet ouvrage.)
- James B. Hartle ; Gravity — An introduction to Einstein's general relativity, Addison-Wesley (2003), ISBN 0-8053-8662-9. Kip Thorne a écrit de ce livre : « la meilleure introduction à la relativité générale jamais écrite » ! L'auteur est professeur de physique théorique à l'université de Santa-Barbara.
- Edwin F. Taylor & John A. Wheeler ; Exploring black holes : introduction to general relativity, Benjammin/Cummings (2000), ISBN 0-201-38423-X. Pour un lecteur qui connait les principes de la relativité restreinte, Wheeler et Taylor introduisent les idées de la relativité générale à partir du concept de trou noir, en utilisant le minimum de mathématiques possible : métriques, algèbre, calcul différentiel et intégral de base (pas de géométrie différentielle, ni de tenseurs).
- Marc Lachièze-Ray ; Initiation à la cosmologie, Masson (2e édition-1996), ISBN 2-225-85208-1. Par un spécialiste du sujet, c'est une introduction très claire et élémentaire au sujet.
- Comittee on Gravitational Physics ; Gravitational Physics — Exploring the structure of space and time, National Academy Press (Washington, D.C.-1999), ISBN 0-309-06635-2. Rapport officiel du Comittee on Gravitational Physics de la National Academy of Sciences américaine, qui comprend quelques-uns des meilleurs spécialistes actuels du domaine. Ce petit ouvrage retrace d'une part les avancées de la recherche ayant eu lieu ces dix dernières années dans le champ de la gravitation — en relation avec l'astrophysique, la cosmologie et la physique des particules — et, d'autre part, propose des pistes de recherche pour la décennie à venir. Une excellente synthèse de l'état de l'art, sans équations.
- Carlo Rovelli, What is Time? What is Space?, Di Renzo Editore, Roma, ISBN 88-8323-146-5
- (en) Ray d’Inverno : Introducing Einstein’s Relativity, Oxford University (1993).
Ouvrages techniques
- Lev Landau et Evguéni Lifchitz, Physique théorique, tome 2 : Théorie des champs, éd. MIR, Moscou [détail des éditions] : second tome du célèbre cours écrit par Landau, théoricien soviétique prix Nobel de physique 1962. Ce volume débute par une introduction à la théorie de la relativité restreinte, se poursuit par la théorie de Maxwell du champ électromagnétique, et expose dans la dernière partie la théorie de la relativité générale. Le niveau reste toujours élevé (second cycle universitaire) : Landau n'ayant pas pour habitude de détailler les calculs intermédiaires, c'est souvent au lecteur de remplir les trous !
- Steven Weinberg ; Gravitation & Cosmolgy, John Wiley & Sons (New York-1972), ISBN 0-471-92567-5. Un très bel ouvrage de référence. Niveau second cycle universitaire minimum.
- C. W. Misner, Kip Thorne & John Wheeler ; Gravitation, Freeman & Co. (San Francisco-1973), ISBN 0-7167-0344-0. Autre ouvrage de référence, qui développe les aspects géométriques modernes avec une grande clarté. Niveau second cycle universitaire minimum.
- (en) Robert M. Wald, General Relativity, University of Chicago Press, 1984, 498 pages (ISBN 0226870332). Plus récent que les deux bibles précédentes, voilà un livre d'introduction à la théorie dans un exposé résolument moderne, qui contient également des développements récents (théorèmes de singularités), incluant certains effets quantiques en gravitation (évaporation des trous noirs d'Hawking). La première partie de ce livre est accessible à partir d'un second cycle universitaire.
- Giuseppe Arcidiacono. Projective Relativity, Cosmology and Gravitation, Di Renzo Editore, Roma, 2006, ISBN 88-8323-153-8
- Ignazio Ciufolini & John A. Wheeler ; Gravitation & Inertia, Princeton Series in Physics, Princeton University Press (1995), ISBN 0-691-03323-4. Un ouvrage consacré à la théorie de la relativité générale, qui débute par un exposé d'introduction classique, et qui se poursuit par l'exploration des développements théoriques plus récents, en prenant en compte les derniers résultats expérimentaux. Niveau second cycle universitaire minimum.
- Clifford M. Will ; Theory & Experiment in gravitational physics, Cambridge University Press (1981), ISBN 0521439736. Une monographie qui contient les aspects techniques des résultats discutés dans l'ouvrage précédent. Niveau second cycle universitaire minimum.
- Sean M. Carroll ; Spacetime and Geometry : An Introduction to General Relativity, Addison Wesley (2003), ISBN 0-8053-8732-3. Une introduction moderne ; une ébauche du texte est disponible sur l'ArXiv : gr-qc/9712019.
- Stephen W. Hawking & Georges F.R. Ellis ; The large scale structure of space-time, Cambridge Monograph on Mathematical Physics, Cambridge University Press (1973), ISBN 0-521-09906-4. Un ouvrage qui expose notamment les théorèmes de singularités démontrés dans les années 1960-70 par Hawking & son mentor Roger Penrose. Niveau troisième cycle universitaire.
- Subrahmanyan Chandrasekhar ; The mathematical theory of black holes, Oxford University Press (1983), ISBN 0-19-850370-9. La théorie mathématique des trous noirs, par le grand astrophysicien théoricien d'origine indienne. Niveau troisième cycle universitaire.
- Philip James Edwin Peebles ; Principles of physical cosmology, Princeton Series in Physics, Princeton University Press (1993), ISBN 0-691-01933-9. Une synthèse récente de la cosmologie. Niveau second cycle universitaire minimum.
- Albert Einstein : Die Grundlage der allgemeinen Relativitätstheorie. In : Annalen der Physik. 49, 1916, p.  ;769–822 (Facsimile, PDF)
- Albert Einstein ; La théorie de la relativité restreinte et générale, Dunod (2005), ISBN 2-10-048716-7. La version anglaise se trouve sur le projet Gutenberg
- Albert Einstein ; Quatre conférences sur la théorie de la relativité, Dunod (2005), ISBN 2-10-049229-2. Texte de quatre conférences prononcées à l'université de Princeton en 1921.
- Hermann Weyl ; Space, time, matter, Dover Publications, Inc. (4e édition-1952), ISBN 0-486-60267-2. Un classique de la physique théorique, écrit par un grand mathématicien. Niveau second cycle universitaire. (Il a existé autrefois une traduction française de cet ouvrage.)
- Stephen W. Hawking & Roger Penrose ; La nature de l'espace et du temps, Collection Essais, Gallimard (1997), ISBN 2-07-074465-5. Ce livre présente les réflexions récentes des deux auteurs, qui tentent chacun de concilier la relativité générale et la théorie quantique. Bien que contenant très peu d'équations, ce livre, sorti dans une collection généraliste qui se veut accessible, est d'un abord très difficile. Niveau troisième cycle universitaire.
Aspects historiques
- Jean Eisenstaedt ; Einstein & la relativité générale — Les chemins de l'espace-temps, CNRS éditions (2002), ISBN 2-271-05880-5. Une histoire érudite de la théorie d'Einstein écrite par Le spécialiste français du domaine.
- (en) W. Perret and G.B. Jeffrey, trans. : The Principle of Relativity : A Collection of Original Memoirs on the Special and General Theory of Relativity, New York Dover (1923), ISBN .
- Wolfgang Pauli ; Theory of relativity, Dover Publications, Inc. (1981), ISBN 0-486-64152-X. Ce livre est une mine d'informations. Il s'agit de la réédition anglaise d'un article de revue écrit en allemand en 1921 pour l’Encyklopädie der Mathematischen Wissenschaften par un jeune théoricien autrichien, alors âgé de 21 ans, étudiant à Göttingen avec Max Born. Voilà ce qu'en dit Einstein dans une lettre adressée à Born datée du 30 décembre 1921 : « Pauli est un type épatant pour ses 21 ans ; il peut être fier de son article pour l'Encyclopédie. »
- Max Jammer ; Concepts of space — The history of theories of space in physics, Dover Publications, Inc. (3e édition-1993), ISBN 0-486-27119-6. Une histoire érudite du concept d'espace, depuis l'Antiquité jusqu'à nos jours.
- Luciano Boi ; Le problème mathématique de l'espace — Une quête de l'intelligible, Springer-Verlag (1995), ISBN 3-540-58922-8. Une histoire philosophique du concept mathématique d'espace, de la géométrie euclidienne au développement des géométries modernes non euclidiennes, dont la version riemannienne est indispensable pour la formulation de la relativité générale. Niveau premier cycle universitaire minimum.
- Marvin J. Greenberg ; Euclidean & Non-Euclidean geometries — Development & History, W.H. Freeman & Co., New-York (3e édition-1996), ISBN 0-7167-2446-4. Un livre de mathématiques qui retrace l'histoire et le développement des géométries non euclidiennes, essentiellement à deux dimensions (géométries de Gauss, Bolai et Lobachevsky). Accessible à l'« honnête homme cultivé ».
- Jean-Pierre Luminet & A. Grib (eds.) ; Essais de cosmologie, collection Source du savoir, Le Seuil (1997), ISBN 2-02-023284-7. Textes fondateurs d'Alexandre Friedmann et de Georges Lemaître (datant de 1923 à 1945) annotés par les éditeurs.
- Henri Poincaré ; La science et l'hypothèse, Collection Champs, Flammarion (1989), ISBN . Un ouvrage classique de philosophie des sciences au format poche, par un très grand mathématicien (mort en 1912). Contient quelques réflexions sur l'espace, ainsi que sur les grandes théories physiques.
Biographies d'Einstein
- Banesh Hoffmann ; Albert Einstein, créateur et rebelle, Collection Points-Sciences, Le Seuil (1975) ISBN 2-02-005347-0. Une excellente biographie au format poche, par un ancien collaborateur d'Einstein à l'Institute for Advanced Studies de Princeton.
- Philippe Frank ; Einstein — Sa vie et son temps, Collection Les savants & le monde, Albin Michel (Paris-1950). Réédition en poche dans la collection Champs, Flammarion (1993) ISBN 2-08-081242-4. Une biographie autorisée de première main, par celui qui fut le successeur d'Einstein à la chaire de physique théorique de l'Université de Prague, nommé sur sa recommandation. Très documentée, elle décrit admirablement le contexte historique (scientifique et politique) de la genèse des travaux d'Einstein.
- Abraham Pais ; Albert Einstein — Sa vie, son œuvre, Interéditions (1993). Réédité par Dunod (2005) ISBN 2-10-049389-2. La biographie scientifique qui fait aujourd'hui autorité depuis sa parution en 1982, par un professeur de l'Université de Rockfeller qui a connu Einstein dans les dernières années de sa vie. Contenu extrêmement riche. Le niveau de certains passages techniques est celui d'un second cycle universitaire (au moins).
- Françoise Balibar ; Einstein : La joie de la pensée, collection Découvertes, Gallimard (1993), ISBN 2-07-053220-8.
- Jacques Merleau-Ponty ; Einstein, Collection Champs, Flammarion (1997) ISBN 2-08-081338-2. Une autre biographie au format poche, par un professeur d'épistémologie de l'Université de Paris X — Nanterre. L'ouvrage est divisé en trois parties : l'homme, son œuvre scientifique et sa philosophie.
Machines temporelles
- Jean-Pierre Luminet ; Les trous noirs, Collection Points-Sciences, Le Seuil (1992), ISBN 2-02-015948-1. Un ouvrage au format poche, par un expert français de l'Observatoire de Meudon travaillant sur le sujet. Introduit l'éventuelle possibilité de voyager dans le temps au moyen de trous de ver.
- Kip S. Thorne ; Trous noirs & distorsions du temps — L'héritage sulfureux d'Einstein, Nouvelle Bibliothèque Scientifique, Flammarion (1997). Réédité dans la collection Champs (2001), ISBN 2-08-081463-X. Un livre essentiellement consacré aux trous noirs, par un spécialiste du genre, professeur de physique théorique au Californian Institute of Technology. Le dernier chapitre présente les recherches les plus récentes (et spéculatives) de l'auteur sur les voyages dans le temps.
- Paul Davies ; How to build a time machine ?, Allen Lane / The Penguin Press (London-2001), ISBN 0-7139-9583-1. Courte revue des possibilités théoriques du voyage dans le temps, par un ancien professeur à l'Université d'Adélaïde. Vulgarisation.
- J. Richard Gott ; Time travel in Einstein's universe — The physical possibilities of travel through time, Weidenfeld & Nicholson (Londres-2001), ISBN 0-297-60760-X. Exploration des possibilités théoriques du voyage dans le temps, par un professeur d'astrophysique à l'Université de Princeton qui a découvert l'une de ces possibilités (utilisation d'une corde cosmique). Vulgarisation.
- Matt Visser ; Lorentzian Wormholes : From Einstein to Hawking, Series in computational and applied mathematical physics, American Institute of Physics (1995), ISBN 1-56396-394-9.
- Igor D. Novikov ; The River of Time, Cambridge University Press (2e édition — 2001), ISBN 0-521-00848-4. Ouvrage écrit par un brillant astrophysicien russe.
- Jim Al-Khalili ; Black Holes, Wormholes & Time Machines, Institute of Physics Publishing (1999), ISBN 0-7503-0560-6. Vulgarisation.
- John Gribbin ; In Search of the Edge of Time : Black Holes, White Holes, Wormholes, Penguin Books (2e édition — 1999), ISBN 0-14-024814-5. Après des études d'astrophysique à l'université de Cambridge, l'auteur est devenu un écrivain scientifique à temps plein.
- Paul J. Nahin ; Time Machines : Time Travel in Physics, Metaphysics, and Science Fiction, American Institute of Physics (2e édition — 2001), ISBN 0-387-98571-9. Ce livre est écrit par un journaliste, pas par un physicien théoricien : certains lecteurs en sont sortis très déçus ! Il contient cependant de nombreuses références. Préface de Kip S. Thorne.
Catégories :- Relativité générale
- Théorie de la gravitation
- Astronomie fondamentale
- Albert Einstein
Wikimedia Foundation. 2010.