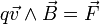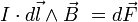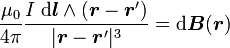Regle de la main droite

La règle de la main droite est un moyen de se rappeler comment sont liées diverses directions. Elle utilise les doigts de la main. Il y a deux règles (les plus connues) : celle qui imite un tire-bouchon avec une rotation et une translation, et, celle qui indique un repère orthonormé direct. Ces règles sont très riche et permettent en électromagnétisme de déterminer le sens et la direction des forces de Laplace(moteurs...), de Lorentz(particules chargées déviées), de la fem induite par la loi de Faraday, de donner la forme et la direction des lignes de champ magnétique produites par un courant, entre autres.

Sommaire 1 Imitation d'un tire bouchon 2 Repère Orthonormal Direct 2.1 Principe 2.2 Force de Lorentz 2.3 Force de Laplace 2.4 Loi de Biot et Savart 3 Voir aussi

Imitation d'un tire bouchon

Dans ce cas, le pouce indique une translation et l'index une rotation.

Exemple, la vis :

• index = le sens de rotation
• pouce = le sens de déplacement / translation

Ou,

le vecteur Champ magnétique B créé par une spire parcourue par un courant :

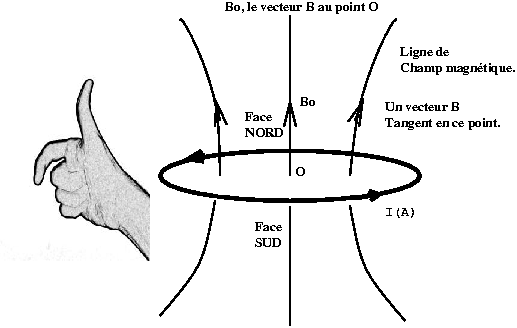
1. pouce - sens du vecteur champ magnétique créé DANS la spire .
2. index ou les 4 doigts autre que le pouce - sens du courant .

Repère Orthonormal Direct

Principe

La règle de la main droite permet de se représenter facilement un repère orthonormal direct. Le pouce, l'index et le majeur permettent de représenter les trois vecteurs de la base appelé couramment 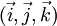ou encore 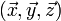. Les trois doigts forment alors un trièdre dans l'espace.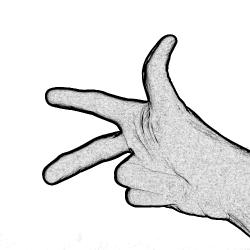

Par définition, 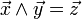. On peut donc choisir, par exemple,

• pouce =
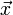
• index =
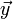
• majeur =

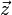
Comme c'est un produit vectoriel, toute permutation directe des vecteurs ne changent pas l'égalité. Ainsi, si l'on veut un 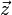associé à une direction verticale ascendante représentée par le pouce, l'index représentera 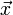et le majeur .

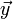Force de Lorentz

Cette règle permet d'interpréter géométriquement le phénomène d'induction de Lorentz (conducteur électrique en mouvement dans un champ magnétique constant) régit par la formule :

La force de Lorentz 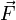s'exerce sur les porteurs de charge et explique la naissance d'une f.e.m. induite dans le circuit en mouvement générant un courant circulant dans la même direction que la force de Lorentz. 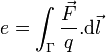. Ce phénomène peut aussi s'expliquer par la loi de Faraday.

En appliquant la règle de la main droite afin de se représenter ce produit vectoriel dans l'espace, on obtient:

• pouce = mouvement du conducteur
• index = champs magnétique
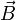
• majeur = courant induit

Les anglophones utilisent le terme de règle de la main droite de Fleming.

Force de Laplace

Dans le domaine de l'induction, la règle de la main droite est aussi appliquée au produit vectoriel de la force de Laplace :

Par exemple, une tige mobile supporté par un rail conducteur circulaire dans un champ magnétique 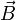et parcouru par un courant 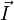pourra subir une translation due à la force de Laplace exercée sur elle. La direction du champ magnétique nécessaire à une translation désirée de la tige peut être déterminée géométriquement par la règle de la main droite. Ce montage est appelé rails de Laplace.

Loi de Biot et Savart

Le champs magnétique 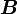créé par une spire respecte la loi de Biot et Savart:

On considère que la spire appartient au plan de repère 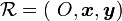. Le courant circule dans le sens inverse des aiguilles des montres (sens trigonométrique). En prenant l'index pour réprésenter le sens du courant à point quelconque 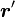de la spire, et le majeur pour le vecteur 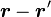où 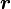désigne un point à l'intérieur dans la spire, le pouce indiquera la direction du champ magnétique créé par la spire (selon l'axe 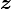). On retrouve le tire-bouchon de maxwell.

Voir aussi

• Tire-bouchon de Maxwell
• Bonhomme d'Ampère
• Orientation
• Symbole de Levi-Civita
• Règle de la main gauche