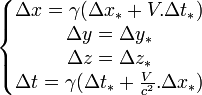- Principe de covariance générale
-
Principe de relativité
 Pour les articles homonymes, voir relativité.
Pour les articles homonymes, voir relativité.
Cet article de physique fait
partie de la série relativitéAvant Einstein Histoire de la physique Michelson - Lorentz Mach - Poincaré - Hilbert exp:Michelson et Morley - éther Avec Einstein Principe de relativité Principe d'équivalence c - transformation de Lorentz espace-temps - E=mc² - temps exp:pensée?-jumeaux-train relativité restreinte-générale controverse historique En physique des particules cyclotron accélérateur de particules Feynman - EQR Méta Formulaire de physique Tous les articles sur la relativité Le principe de relativité[1], affirme que les lois physiques s'expriment de manière identique dans tous les référentiels inertiels.
- Ce qui implique que pour deux expériences préparées de manière identique dans deux référentiels inertiels, les mesures faites sur l'une et l'autre dans leur référentiel respectif sont identiques.
- Cela ne signifie pas que les mesures au cours d'une expérience sont les mêmes pour les différents observateurs, chacun mesurant depuis son référentiel inertiel respectif, mais cela implique que les mesures faites par les différents observateurs vérifient les mêmes équations, un changement de référentiel pour l'observation intervenant sous la forme de la variation d'un ou plusieur paramètres dans les équations. On dit que les lois sont « invariantes par changement de référentiel inertiel ».
Une généralisation à la base de la relativité générale, et appelée principe de covariance[2] ou principe de relativité générale[3],[4], affirme que les lois physiques s'expriment de manière identique dans tous les référentiels (inertiels ou non). On dit alors que les lois sont « covariantes ».
D'une théorie à l'autre (physique classique, relativité restreinte ou générale), la formulation du principe a évolué et s'accompagne d'autres hypothèses sur l'espace et le temps, sur les vitesses, etc. Certaines de ces hypothèses étaient implicites ou « évidentes » en physique classique, car conformes à toutes les expériences, et elles sont devenues explicites et plus discutées à partir du moment où la relativité restreinte a été formulée.
Sommaire
Exemples en physique classique
- Première situation
Supposons que dans un train en marche, un voyageur se tienne debout, immobile par rapport à ce train, et tienne un objet dans la main. S’il lâche l’objet, celui-ci tombe à la verticale de la main qui le tenait (vitesse initiale par rapport au train nulle) et selon une certaine loi en fonction du temps.
Le principe de relativité ne dit pas que le mouvement de cet objet sera le même si, après l’avoir rapporté à un référentiel lié au train on le rapporte à un référentiel lié au sol : l’expérience montre que ce serait erroné puisque, vu du train l’objet décrit une droite verticale, tandis que, vu du sol il décrit une parabole.
L'expérience vue depuis l'un ou l'autre de ces référentiels les conditions initiales ne sont pas les mêmes : l'attraction gravitationnelle est identique dans les deux, mais par rapport au référentiel lié au train la vitesse initiale de l’objet lâché est nulle, tandis que par rapport à celui référentiel lié au sol, elle ne l’est pas.
Toutefois, une même loi mathématique pour chacun des deux référentiels permet de décrire cette expérience, cette loi tient compte de la vitesse initiale par rapport au référentiel.
- Deuxième situation
En revanche, si quelqu’un, immobile par rapport au sol, lâche un objet qu’il tient dans la main, le principe de relativité s’applique car les conditions générales ainsi que les conditions initiales sont identiques : selon le principe de relativité l’objet doit tomber par rapport au sol selon une droite verticale et selon la même loi que dans le cas où il est lâché dans le train : c’est bien ce que l’expérience confirme.
- Conclusion
Dans les deux cas exposés, le principe de relativité s'applique différemment : pour l'expérience vue depuis deux référentiels différents, les observations sont différentes mais une même loi mathématique les décrit toutes les deux (où il est tenu compte de la vitesse initiale, nulle ou non) ; pour les deux expériences faites dans deux référentiels distincts, où les conditions de l'expérience sont identiques, les observations sont rigoureusement identiques (aux imprécisions de mesures près).
Formulations
En mécanique classique
Définition : Un référentiel galiléen (ou inertiel) est un référentiel dans lequel tout corps libre (non influencé par l'extérieur) qui est au repos y reste indéfiniment, et tout corps libre en mouvement reste à vecteur vitesse constant (et donc aussi à moment angulaire constant).
Principe de relativité de Galilée : toutes les lois de la mécanique sont identiques dans tous les référentiels galiléens.
Hypothèses sur l'espace physique : l'espace physique, supposé homogène et isotrope, est identifié à un espace affine de dimension 3, on utilise alors l'espace vectoriel associé, le temps paramétrant les trajectoires et les états du système étudié.
Propriété : soit (R) est un référentiel galiléen, on a : si (R * ) est un référentiel se déplaçant par translation à vitesse constante V par rapport à (R), alors (R * ) est lui aussi galiléen.
Remarque : on prendra garde au fait que la réciproque de la propriété n'est pas vraie, contrairement à ce qui a semblé évident à tous jusqu'à ce qu'Albert Einstein élabore le principe d'équivalence.Commentaire : le principe a ici deux significations.
- Qu'une même expérience vue depuis les deux référentiels galiléens différents, (R) et (R * ), suit une loi qui s'exprime de la même manière quand elle est formulée dans les coordonnées de l'un ou de l'autre des référentiels.
- Et aussi qu'une expérience faite à l'identique dans deux référentiels galiléens quelconques suit, dans chacun, la même loi et donne exactement les mêmes observations.
Hypothèse pour les changement de référentiel : les transformations de Galilée.
Si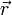 est le vecteur coordonnées d'un point dans (R) et
est le vecteur coordonnées d'un point dans (R) et 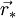 est le vecteur coordonnées du même point dans (R * ), alors on a :
est le vecteur coordonnées du même point dans (R * ), alors on a :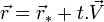 et
et 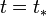
-
- Remarque : cette hypothèse a été tellement longtemps en parfait accord avec toutes les expériences qu'elle a été une évidence jusqu'à la formulation de la relativité restreinte. Par ailleurs, elle implique qu'il n'y a pas de vitesse maximale, ce qui était en accord avec les observations sur la vitesse infinie (semblait-il) de la transmission de l'influence gravitationnelle.
Le principe de relativité de Galilée s'exprime aussi bien comme la nécessité de l'invariance des équations du mouvement par rapport aux transformations de Galilée.
- La deuxième égalité signifie que le temps est le même dans les deux référentiels[note 1].
- La première égalité[note 2] est équivalente à la loi de composition des vitesses :
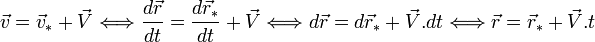 (à un vecteur constant près)
(à un vecteur constant près) - Elle est aussi équivalente à l'indépendance de l'accélération (et donc de la force
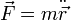 s'exerçant sur le corps) par rapport au référentiel inertiel de l'observateur :
s'exerçant sur le corps) par rapport au référentiel inertiel de l'observateur : 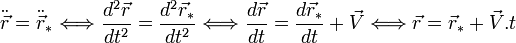 (à un vecteur constant près)
(à un vecteur constant près)
Exemple du choc élastique de deux corps ponctuelsDans un référentiel inertiel, deux corps ponctuels libres, donc ayant une vitesse uniforme, se heurtent en un choc élastique (pas de déperdition d'énergie en chaleur ou autre). On suppose que la masse de chaque corps est conservée au cours du choc.
Phénomènes observés suivant le référentiel choisi :
Dans le référentiel inertiel du centre d'inertie : les deux corps se rapprochent l'un de l'autre frontalement sur la même ligne droite et repartent l'un et l'autre à la même vitesse qu'avant le choc mais dans le sens opposé.
Dans le référentiel d'un des corps avant le choc : le deuxième corps s'approche du premier (qui est immobile) et, après le choc, le premier corps est animé d'un mouvement alors que le second est ralenti ou repart dans l'autre sens.
Dans un référentiel inertiel quelconque : les deux corps, l'un et l'autre à vitesse constante, se heurtent au cours de leur mouvement, changent de direction et de vitesse.
Loi générale valable dans tout référentiel inertiel : d'après la conservation de la quantité de mouvement, la vitesse du centre d'inertie du système constitué des deux masses m1 et m2 est égale à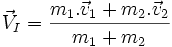 et est constante et inchangée avant et après le choc, et les vitesses après le choc sont : pour la masse n°1
et est constante et inchangée avant et après le choc, et les vitesses après le choc sont : pour la masse n°1 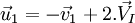 et pour la masse n°2
et pour la masse n°2 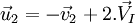
Un changement de référentiel de (R) vers (R * ) imposant le changement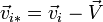 et
et 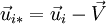 , pour i=1;2 , laisse bien inchangée la loi énoncée ci-dessus.
, pour i=1;2 , laisse bien inchangée la loi énoncée ci-dessus.
On constate donc que les phénomènes observés diffèrent d'un référentiel à l'autre, mais dans tous la loi vérifiée par les vitesses mesurées est la même.
Bien sûr dans le cas de masses non ponctuelles, et autres cas plus réalistes, cette loi n'est qu'une approximation.Exemple d'un corps, dans le vide, soumis à un champ de gravitation uniforme- Dans le référentiel (R * ) :
- La force est
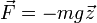 , où
, où 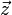 est le vecteur unitaire de la verticale au sol; l'équation de la dynamique est
est le vecteur unitaire de la verticale au sol; l'équation de la dynamique est 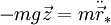 , et l'équation du mouvement est
, et l'équation du mouvement est 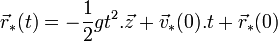
- Utilisation des transformations de Galilée pour obtenir la loi dans le référentiel (R) :
- Sachant que l'on a
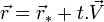 (ce qui sous-entend que
(ce qui sous-entend que 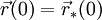 , ce qui est une petite restriction par rapport à la généralité), on obtient :
, ce qui est une petite restriction par rapport à la généralité), on obtient : 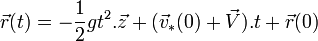 , puis, en utilisant l'égalité
, puis, en utilisant l'égalité 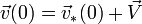 on a bien la même loi dans le référentiel (R) :
on a bien la même loi dans le référentiel (R) : 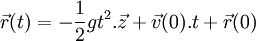
- Bien sûr, on peut aussi utiliser les expressions de
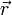 et
et 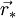 déduites des équations différentielles, et montrer que
déduites des équations différentielles, et montrer que 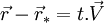 , ou plus directement déduire cette égalité du fait que
, ou plus directement déduire cette égalité du fait que 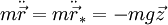 : en effet, de
: en effet, de 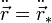 on obtient
on obtient 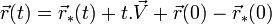 , ce qui est la transformation de Galilée dans toute sa généralité, et la démonstration réciproque ne pose pas de problème.
, ce qui est la transformation de Galilée dans toute sa généralité, et la démonstration réciproque ne pose pas de problème.
Exemple d'un corps soumis aux seuls frottements de l'airDans le référentiel (R * ) la force est schématisée par
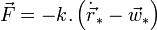 , où
, où 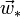 est la vitesse (constante) du référentiel par rapport au référentiel (inertiel) où l'air est immobile (et homogène, etc...) : en effet, les frottements dépendent de la vitesse du corps par rapport à l'air, et non pas de la vitesse du corps par rapport au référentiel (R * ).
est la vitesse (constante) du référentiel par rapport au référentiel (inertiel) où l'air est immobile (et homogène, etc...) : en effet, les frottements dépendent de la vitesse du corps par rapport à l'air, et non pas de la vitesse du corps par rapport au référentiel (R * ).
La loi qui en découle est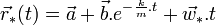 , où
, où 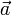 et
et 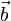 sont des vecteurs constants déterminés par les conditions initiales du mouvement.
sont des vecteurs constants déterminés par les conditions initiales du mouvement.
Cette loi est invariante par la transformation de Galilée, comme on le vérifie facilement.Exemple d'une onde monochromatique dans un fluide compressibleDans un fluide compressible, immobile dans le référentiel galiléen (R * ), la fonction d'onde monochromatique est
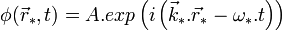 , avec
, avec 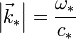 où
où 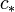 est la vitesse de propagation de l'onde.
est la vitesse de propagation de l'onde.
Pour déterminer la fonction d'onde dans le référentiel (R), on utilise la transformation de Galilée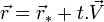 , et on obtient :
, et on obtient : 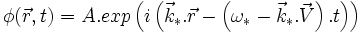 .
.
D'où :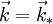 ;
; 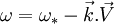 ;
; 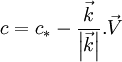 Contre-exemple : la lumière
Contre-exemple : la lumièreEn physique classique, le principe de relativité ne concerne que la mécanique, donc est exclut d'application à l'électromagnétisme et à la lumière (mais s'applique à l'optique géométrique). Mais les interactions entre particules chargées et ondes électromagnétiques obligent à étudier simultanément ce principe et l'électromagnétisme.
La lumière, si elle est envisagée comme une onde (électromagnétique) se propageant dans un milieu appelé l'éther, doit avoir une fonction d'onde (monochromatique) vérifiant les propriétés vues ci-dessus : sa vitesse n'est pas la même dans tous les référentiels galiléens, ni dans toutes les directions
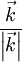 .
.
Mais les équations de Maxwell donnent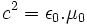 où
où 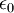 est la permittivité diélectrique du vide et
est la permittivité diélectrique du vide et 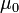 la perméabilité magnétique du vide sont des constantes caractéristiques du vide, à priori, indépendantes du référentiel utilisé. Dès lors un choix s'impose :
la perméabilité magnétique du vide sont des constantes caractéristiques du vide, à priori, indépendantes du référentiel utilisé. Dès lors un choix s'impose :- Soit les équations de Maxwell ont été calculées implicitement dans un référentiel privilégié : celui où le milieu de propagation, l'éther, est immobile. Dans ce cas la lumière vérifie les propriètés des ondes vues ci-dessus.
- Soit les équations de Maxwell sont valables dans tous les référentiels galiléens et la vitesse de la lumière y est la même dans tous et dans toutes les directions. Dans ce cas, d'importantes révisions s'imposent en ce qui concerne la mathématisation du principe de relativité.
En relativité restreinte
La définition d'un référentiel galiléen est la même qu'en mécanique classique.
Le principe de relativité voit son domaine d'application s'élargir :
Principe de relativité : toutes les lois de la physique, hormis la gravitation, sont identiques dans tous les référentiels galiléens.On y joint un postulat conforme à l'électromagnétisme de Maxwell : « la vitesse de la lumière dans le vide ne dépend pas de la vitesse de sa source », que l'on peut aussi exprimer « la valeur de la vitesse de la lumière dans le vide est la même dans tous les référentiels galiléens ».
- La gravitation : jusqu'à la relativité générale, la loi universelle de la gravitation de Newton et l'avance du périhélie de Mercure ne furent pas compatibles avec le postulat sur la vitesse de la lumière et les hypothèses sur l'espace.
- Remarque : Les mathématiques proposent, avec le seul principe de relativité (dans un espace affine), d'avoir une vitesse inchangée d'un référentiel galiléen à l'autre et indépassable, cette vitesse étant, au choix, finie ou infinie. Les propriétés de la vitesse de la lumière, qui est finie dans la théorie de l'électromagnétisme, permettent son identification avec la vitesse limite de la théorie.
Hypothèses sur l'espace physique : l'espace physique est supposé homogène et isotrope et est identifié, pour chaque référentiel galiléen, à un espace affine (avec l'espace vectoriel associé) de dimension 3, et un temps paramètrisant les trajectoires et les états du système étudié : la mesure du temps est propre à chaque référentiel et les changements de référentiels indiquent aussi le changement de cette mesure. L'hypothèse sur la vitesse de la lumière impliquant que chaque référentiel galiléen a son propre temps, l'espace physique peut aussi être identifié à un espace-temps de quatre dimensions (trois d'espace et une de temps) : l'espace-temps de Minkowski.
La propriété est toujours vraie :
Propriété : soit (R) est un référentiel galiléen, on a : si (R * ) est un référentiel se déplaçant par translation à vitesse constante V par rapport à (R), alors (R * ) est lui aussi galiléen.- Remarque : la réciproque de la propriété est implicitement admise. En relativité restreinte les référentiels étudiés sont ceux qui sont inertiels et qui sont supposés en translations à vitesse constante les uns par rapport aux autres. La gravitation n'est pas traitée par cette théorie.
Commentaire : pour le principe de relativité, idem au commentaire fait dans le paragraphe ci-dessus de la mécanique classique. Pour le second principe : on peut en comprendre la nécessité si on considère que la vitesse de la lumière est une mesure de deux expériences identiques (émission de lumière) faites dans deux référentiels galiléens différents : sa mesure doit être la même dans les deux (mais pour admettre cela il faut s'être convaincu que l'éther n'a pas sa place en physique).
Conséquences : la vitesse de la lumière dans le vide est une vitesse indépassable dans tout référentiel; deux évènements simultanés dans le référentiel (R) peuvent ne pas l'être dans (R * ); les mesures des intervalles de temps, des longueurs, des vitesses et des accélérations changent d'un référentiel à l'autre[note 3]; etc.
Transformations de Lorentz : ces transformations, déductibles des hypothèses, expriment les changements des mesures des intervalles de temps, des longueurs et des vitesses d'un référentiel inertiel à l'autre; le principe de relativité, en relativité restreinte, s'exprime aussi comme la nécessité de l'invariance des équations de la physique par ces transformations.
Le diagramme de Minkowski permet de visualiser les différents effets de la relativité en évitant de manipuler trop de formules mathématiques.
Transformations de LorentzArticle détaillé : Transformation de Lorentz.Les coordonnées et le temps dans (R) étant
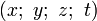 , et dans (R * ) étant
, et dans (R * ) étant 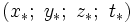 , on suppose que la vitesse relative V entre les deux référentiels est de même direction que l'axe des x.
, on suppose que la vitesse relative V entre les deux référentiels est de même direction que l'axe des x.-
- En posant
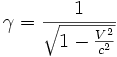 , les transformations de Lorentz sont :
, les transformations de Lorentz sont :
- En posant
-
-
- Loi de composition relativiste des vitesses :
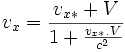
-
Relativité du temps et temps propreArticle détaillé : temps propre.La constance de la vitesse de la lumière dans le vide d'un référentiel (inertiel, comme toujours ici) à l'autre permet de définir la même unité de mesure du temps dans tous les référentiels quand est bien défini une unité de mesure commune des longueurs.
- Ainsi, pour être sûr que deux référentiels, en mouvement rectiligne uniforme l'un par rapport à l'autre, utilisent la même longueur unitaire, on peut considérer une longueur perpendiculaire à la vitesse relative : la longueur de référence sera ainsi matériellement commune aux deux référentiels (comme la hauteur d'une porte coulissante tenue par deux rails vissés l'un au sol et l'autre au plafond).
- Avec ce mécanisme qui compte comme unité de temps la moitié de l'intervalle de temps mis par la lumière pour faire l'aller-retour le long de la longueur commune, on peut considérer que l'on a simplement une montre identique dans chaque référentiel.
- Dans les dessins suivants, chaque référentiel voit pour lui le phénomène de gauche, et du premier on voit dans l'autre le phénomène de droite.
- Dans le dessin de gauche, le temps mesuré est le temps propre : le temps mesuré entre deux évènements, dans le référentiel où ils ont lieu au même endroit.
- Dans le dessin de droite, le temps mesuré est impropre : le temps mesuré entre deux évènements dans un référentiel où ils ont lieu en deux endroits différents.
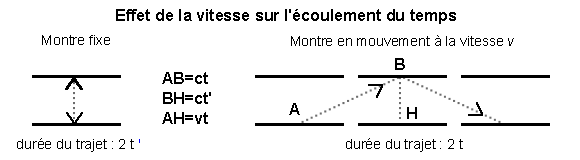
- Dans le deuxième dessin, par le théorème de Pythagore on obtient
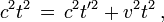 d'où :
d'où : 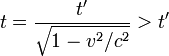 .
.
- Ainsi le temps impropre
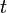 est plus grand que le temps propre
est plus grand que le temps propre 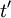 , et celui-ci est le temps minimal mesurable entre deux évènements.
, et celui-ci est le temps minimal mesurable entre deux évènements.
- Mais il semble y avoir un paradoxe : comment peut-il se faire que le temps de (R * ) paraisse ralenti vu depuis (R), et vice-versa ?
- En fait ce n'est pas n'importe quel temps qui semble ralenti, c'est le temps propre entre deux évènements. Pour savoir si le temps (impropre), séparent deux évènements situés en des endroits différents, semble ralenti ou pas vu d'un autre référentiel, il faut concevoir une autre expérience, et la réponse ne sera pas toujours positive. La propriété, vraie pour le temps propre, ne doit pas être abusivement généralisée.
Cette expérience d'écoulement du temps sur une horloge donne des mesures différentes dans le référentiel propre de l'horloge et dans un autre référentiel inertiel.
De manière similaire, la mesure d'une longueur parallèle au mouvement relatif de deux référentiels inertiels donne des résultats différents suivant que la mesure est faite dans l'un ou l'autre des référentiels.À titre d'exemple expérimental, on peut citer des particules élémentaires (tels les muons) ayant une durée de vie très courte quand elles sont immobiles (après 10-6 seconde environ, elles se désintègrent en d'autres particules moins détectables), mais ayant une durée de vie 10 fois plus longue quand elles sont observées à des vitesses proches de celle de la lumière.
Relativité de la longueurArticle détaillé : contraction des longueurs.La mesure d'une longueur donne des résultats différents suivant le référentiel où elle est faite.
Les transformations de Lorentz permettent de le montrer :
- En supposant que les axes des référentiels
 et
et 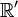 sont parallèles et que la vitesse relative est parallèle à l'axe des x, on a
sont parallèles et que la vitesse relative est parallèle à l'axe des x, on a 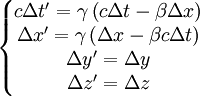
- Donc, si les extrémités de l'objet sont similtanées dans
 , alors
, alors 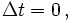 et dans le référentiel
et dans le référentiel  ,
, 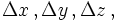 sont les différentes longueurs de l'objet dans les trois dimensions. Alors
sont les différentes longueurs de l'objet dans les trois dimensions. Alors 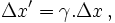 et ainsi
et ainsi 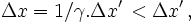 ce qui montre que la longueur mesurée dans
ce qui montre que la longueur mesurée dans  est inférieure à celle mesurée dans
est inférieure à celle mesurée dans 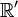 .
.
Ce n'est pas un paradoxe car du fait de la relativité de la simultanéité, la mesure faite dans
 ne semble pas correctement faite quand elle est observée depuis
ne semble pas correctement faite quand elle est observée depuis 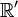 .Relativité de la simultanéitéArticle détaillé : Simultanéité.
.Relativité de la simultanéitéArticle détaillé : Simultanéité.Supposons qu'il y ai deux observateurs des évènements, chacun immobile dans son repère inertiel. Chacun connait parfaitement la distance qui le sépare de chaque point immobile dans le référentiel, donc quand il reçoit une information venant de l'un d'eux, il connait le temps nécessaire à la transmission de l'information (que l'on suppose aller à la vitesse de la lumière) et il peut ainsi déterminer exactement à quel moment c'est passé cet évènement.
Si deux évènements distants se passent simultanément dans le référentiel d'un observateur, dans le référentiel de l'autre, ils ne seront pas simultanés.En effet, d'après les transformations de Lorentz :
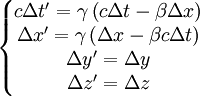
- D'où, si
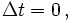 alors
alors 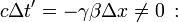 il n'y a donc pas simultanéité dans l'autre référentiel. On peut dire que la simultanéité est relative au référentiel de l'observateur.
il n'y a donc pas simultanéité dans l'autre référentiel. On peut dire que la simultanéité est relative au référentiel de l'observateur.
L'invariant de la relativité restreinteArticle détaillé : Intervalle d'espace-temps.En mécanique non-relativiste, le temps et les longueurs sont des invariants par changement de référentiels inertiels (et même non-inertiels); ce n'est plus le cas en relativité restreinte. Toutefois, une « mesure », mêlant longueur spatiale et temps, est invariante par changement de référentiel : elle est nommée métrique, et elle donne à l'espace-temps une notion de distance entre deux évènements.
Cet invariant est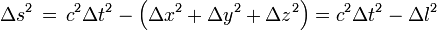 , où
, où 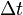 et
et 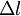 sont respectivement les écarts temporel et spatial entre deux évènements, mesurés dans un référentiel quelconque et
sont respectivement les écarts temporel et spatial entre deux évènements, mesurés dans un référentiel quelconque et 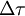 est le temps propre séparent les deux évènements.
est le temps propre séparent les deux évènements.- Dans le cas où les deux évènements peuvent être liés par un lien causal, on a
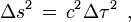 où Δτ est le temps propre les séparant. On justifie facilement avec la formule liant le temps propre et le temps impropre, démontrée dans le paragraphe concernant la relativité du temps, que cette expression de
où Δτ est le temps propre les séparant. On justifie facilement avec la formule liant le temps propre et le temps impropre, démontrée dans le paragraphe concernant la relativité du temps, que cette expression de 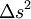 à la même valeur quel que soit le référentiel où les mesures ont été faites : il suffit de changer de notation et d'écrire
à la même valeur quel que soit le référentiel où les mesures ont été faites : il suffit de changer de notation et d'écrire 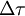 à la place de
à la place de 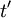 , puis
, puis 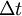 à la place de
à la place de 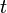 et enfin de définir
et enfin de définir 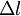 par
par 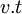 car c'est la distance qui sépare les deux évènements dans le référentiel inertiel non-propre (et quelconque).
car c'est la distance qui sépare les deux évènements dans le référentiel inertiel non-propre (et quelconque).
Cet invariant
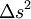 défini ici est parfois défini par
défini ici est parfois défini par 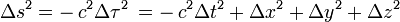 , c'est à dire avec les signes opposés à ceux présentés ici : la signature est ici (+,-,-,-), et on lui préfère parfois la signature (-,+,+,+), et dans ce cas
, c'est à dire avec les signes opposés à ceux présentés ici : la signature est ici (+,-,-,-), et on lui préfère parfois la signature (-,+,+,+), et dans ce cas 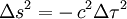 .
.Ainsi, dans un référentiel deux évènements sont éloignés d'une distance
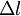 et séparés d'un temps
et séparés d'un temps 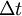 : ces mesures sont différentes d'un référentiel à l'autre, mais pour tous les référentiels l'égalité
: ces mesures sont différentes d'un référentiel à l'autre, mais pour tous les référentiels l'égalité 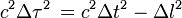 est vérifiée.
est vérifiée.On montre par le calcul que cette métrique est bien invariante par l'application des transformées de Lorentz, et que les transformations affines laissant invariante la métrique forment le groupe de Poincaré, incluant les transformations de Lorentz.
En relativité générale
Vérifier le principe de covariance générale et bien modéliser la gravitation sont les principales raisons d'être de cette théorie.
Principe de relativité ou de covariance générale : les lois de la physique sont identiques dans tous les référentiels.
Définition : Un référentiel inertiel est un référentiel dans lequel tout corps libre (non influencé par l'extérieur) qui est au repos y reste indéfiniment, et tout corps libre en mouvement reste à vitesse constante (et donc aussi à moment angulaire constant). Du fait des autres contraintes indiquées ci-dessous, un tel référentiel ne peut être défini que localement et temporairement.
Commentaire :- Ici, le principe signifie qu'une expérience vérifie une loi qui s'exprime de la même manière (même formule) pour tous les référentiels (galiléens ou non) des différents observateurs.
- Dans les référentiels galiléens, on observe toujours exactement les mêmes résultats pour des expériences identiques; et de manière plus générale, dans deux référentiels soumis exactement au même champ de gravitation et ayant une expérience identiquement faite dans chacun, la loi de l'expérience sera rigoureusement la même dans les deux référentiels, les observations de l'expérience et les mesures aussi.
- Dans des référentiels ayant des contraintes gravitationnelles différentes, les mesures d'une expérience seront influencées par le champ gravitationnel de chaque référentiel, suivant la même loi.
Principe d'équivalence : la gravitation est localement équivalente à une accélération du référentiel, tout référentiel en chute libre dans un champ de gravitation est un référentiel inertiel où les lois physiques sont celles de la relativité restreinte.
Remarque : partant de l'hypothèse qu'il doit y avoir continuité des propriétés avec la relativité restreinte, une expérience par la pensée faite par Einstein lui fit comprendre que dans un référentiel accéléré les mesures des longueurs ne sont pas compatibles avec une géométrie euclidienne, c'est à dire avec un espace plat.
Structure mathématique utilisée : variété riemannienne de dimension 4 (une « surface de dimension 4 » déformée, avec une métrique localement définie), les lois étant écrites avec des égalités tensorielles pour assurer leur validité en tout point de la variété et pour tout référentiel.
Propriété :
- Là où l'espace est courbe (courbure principale non-nulle), les seuls référentiels inertiels sont les référentiels en chute libre dans le champ de gravitation, et ils ne sont inertiels que sur une étendue d'espace-temps localement plate (ce qui n'est jamais qu'une approximation). Dans une telle étendue, la relativité restreinte s'applique et tout référentiel translaté du référentiel inertiel est lui-même inertiel (avec des limitations semblables).
- Là où l'espace est courbe, la notion de translation est remplacée par le déplacement le long d'une géodésique. Mais la notion de distance n'est que locale en relativité générale (hors du cadre local, deux points distincts peuvent être joints par deux géodésiques de longueurs différentes), et il est délicat de vouloir connaitre l'évolution dans le temps (lié à un référentiel) de la distance entre deux référentiels inertiels joints par une géodésique : à priori, la variation d'une telle distance n'est pas proportionnelle au temps écoulé.
- Là où l'espace est plat (pseudo-euclidien), ce qui à priori n'est jamais parfaitement réalisé, la théorie de la relativité restreinte s'applique, mais on peut choisir un référentiel accéléré et ainsi avoir toutes les manifestations locales d'un champ de gravitation.
Conséquences : la gravitation est la manifestation de la déformation de l'espace-temps, déformation réelle si elle est due à l'énergie d'un corps, apparente si elle est due au choix d'un référentiel accéléré, sans qu'un observateur ne puisse distinguer ces deux cas par des données locales; les trajectoires suivies par les particules dans le champ de gravitation sont des géodésiques; les lois de la relativité restreinte, toujours vraies dans les référentiels inertiels, peuvent être généralisées à tous les référentiels en étant exprimées avec des égalités tensorielles et en utilisant le principe de correspondance adéquat;...
En physique quantique
Le principe de relativité n'est pas un principe explicite de la physique quantique, mais toute la construction de cette théorie l'utilise, plus ou moins implicitement.
Ainsi, l'équation de Schrödinger est construite à partir de l'équivalence des principes de moindre action et de Fermat (pour la physique non-relativiste), donc elle respecte le principe de relativité dans le cadre non relativiste.
Les équations de Klein-Gordon et de Dirac ont été construites à partir d'équations de la relativité restreinte, et respectent donc le principe de relativité dans le cadre relativiste (voir Mécanique quantique relativiste).
En physique quantique les symétries et invariances des équations étant écrites à l'aide des notions de groupe de Lie et d'algèbre de Lie, le principe de relativité (invariance par rapport à certaines transformations de l'espace-temps) s'y exprime par l'invariance des équations par le groupe de Poincaré qui est un groupe de Lie.Historique
Plusieurs étapes importantes jalonnent l'histoire de ce principe :
Sa découverte par Galilée
En 1543 est publié l'ouvrage de Nicolas Copernic, De revolutionibus orbium coelestium, qui fonde l'héliocentrisme. Son influence est dans un premier temps assez limitée. En effet, la préface, rédigée par Andreas Osiander, présente le point de vue de Copernic comme un artifice mathématique visant à améliorer les méthodes de calcul des tables astronomiques. Les choses évoluent rapidement au début du XVIIe siècle, avec Kepler qui, en 1609 énonce ses premières lois sur le mouvement des planètes, et avec Galilée, convaincu à partir de 1610 du mouvement de la Terre autour du Soleil. Les conceptions de ce dernier s'opposent à la fois aux dogmes religieux et philosophiques, qui font de la Terre le centre fixe du monde, lieu privilégié de la révélation divine.
Se basant sur des observations, Galilée s'oppose aux partisans d'Aristote, pour lesquels tout mouvement de la Terre est impossible. En effet, selon la physique d'Aristote, si la Terre bougeait, un objet lancé verticalement en l'air ne retomberait pas au lieu d'où il a été lancé, les oiseaux seraient entraînés vers l'ouest, etc... Galilée développe alors un discours visant à réfuter les arguments des aristotéliciens. Il énonce les principes qui fonderont la relativité galiléenne. Plusieurs passages de son ouvrage Dialogue sur deux grands systèmes du monde, publié en 1632 sont consacrés à cette réfutation. Ainsi, selon Galilée, le mouvement n'existe que par rapport à des objets considérés comme immobiles, que de manière comparative : « Le mouvement est mouvement et agit comme mouvement pour autant qu'il est en rapport avec des choses qui en sont dépourvues ; mais pour toutes les choses qui y participent également, il n'agit pas, il est comme s'il n'était pas »[5].
De plus, les résultats d'une expérience ne changent pas, qu'elle se passe sur la terre ferme ou dans la cabine d'un bateau navigant sans heurt ni ballotage.
Extrait du « Dialogue sur les deux grand systèmes du Monde »« Enfermez-vous avec un ami dans la plus grande cabine sous le pont d'un grand navire et prenez avec vous des mouches, des papillons et d'autres petites bêtes qui volent ; munissez-vous aussi d'un grand récipient rempli d'eau avec de petits poissons ; accrochez aussi un petit seau dont l'eau coule goutte à goutte dans un autre vase à petite ouverture placé en dessous. Quand le navire est immobile, observez soigneusement comme les petites bêtes qui volent vont à la même vitesse dans toutes les directions de la cabine, on voit les poissons nager indifféremment de tous les côtés, les gouttes qui tombent entrent toutes dans le vase placé dessous ; si vous lancez quelque chose à votre ami, vous n'avez pas besoin de jeter plus fort dans une direction que dans une autre lorsque les distances sont égales ; si vous sautez à pieds joints, comme on dit, vous franchirez des espaces égaux dans toutes les directions. Quand vous aurez soigneusement observé cela, bien qu'il ne fasse aucun doute que les choses doivent se passer ainsi quand le navire est immobile, faites aller le navire à la vitesse que vous voulez ; pourvu que le mouvement soit uniforme, sans balancement dans un sens ou l'autre, vous ne remarquerez pas le moindre changement dans tous les effets qu'on vient d'indiquer ; aucun ne vous permettra de vous rendre compte si le navire est en marche ou immobile : en sautant, vous franchirez sur le plancher les mêmes distances qu'auparavant, et ce n'est pas parce que le navire ira très vite que vous ferez de plus grands sauts vers la poupe que vers la proue ; pourtant, pendant le temps où vous êtes en l'air, le plancher au-dessous de vous court dans le direction opposée à votre saut ; si vous lancez quelque chose à votre ami, vous n'aurez pas besoin de plus de force pour qu'il le reçoive, qu'il se trouve du côté de la proue ou de la poupe, et pourtant, pendant que la gouttelette est en l'air, le navire avance de plusieurs palmes ; les poissons dans leur eau ne se fatigueront pas plus pour nager vers l'avant que vers l'arrière de leur récipient, c'est avec la même facilité qu'ils iront vers la nourriture que vous aurez disposée où vous voudrez au bord du récipient ; enfin, les papillons et les mouches continueront à voler indifféremment dans toutes les directions, jamais vous ne les verrez se réfugier vers la paroi du côté du la poupe comme s'ils étaient fatigués de suivre la course rapide du navire dont ils auront été longtemps séparés, puisqu'ils restent en l'air ; brûlez un grain d'encens, il se fera un peu de fumée que vous verrez monter vers le haut et y demeurer, tel un petit nuage, sans qu'elle aille d'un côté plutôt que d'un autre. »— Galilée [6]
En langage moderne, le mouvement uniforme (inertiel) du bloc expérience+observateur n'a aucun effet sur l'expérience observée. Ainsi, même si la Terre se déplace, la pierre jetée verticalement retombe aux pieds du lanceur, et les oiseaux volent normalement dans toutes les directions. Ce point de vue constitue une révolution dans les conceptions mécaniques de l'époque. Selon la physique d'Aristote alors communément enseignée, le mouvement et le repos sont deux états différents, et le mouvement nécessite un moteur. Selon Galilée, mouvement et repos sont un même état, différent l'un de l'autre par simple changement de référentiel. Cette conception est à la base du principe d'inertie.
Une particularité aujourd'hui difficile à concevoir : pour Galilée, le véritable mouvement inertiel n'est pas rectiligne mais est circulaire (un grand cercle du globe terrestre)[7]. Signalons également que Galilée, ayant réfuté les arguments aristotéliciens contre le mouvement de la Terre, cherchera quel phénomène observable peut rendre compte de ce mouvement. Il pensera le trouver, de façon erronée, dans une explication des marées. Il faudra plus de deux siècles pour que soient imaginées des expériences mécaniques montrant le mouvement de la Terre par rapport à un référentiel galiléen.
A la suite de Galilée, une des premières utilisations d'un référentiel fictif (non représenté dans l'expérience par un corps quelconque) peut être attribuée à Christiaan Huygens, dans son ouvrage de Motu corporum ex percussione[8]. Ayant pris conscience en 1652 des erreurs de Descartes sur les lois des chocs, il conçoit un repère mobile par rapport auquel on fait une expérience. Cherchant quelles sont les vitesses de deux corps identiques après un choc, alors qu'initialement le premier corps se déplace à la vitesse V et le second à la vitesse V' par rapport au sol, il imagine un observateur se déplaçant à la vitesse (V+V')/2. Cet observateur voit les deux corps se rapprocher à la vitesse (V-V')/2, se heurter, et, étant de même masse, s'éloigner avec la même vitesse. Revenant au référentiel terrestre, Huygens en conclut qu'après le choc, les deux corps ont échangé leur vitesse.
Il est à remarquer que l'additivité des vitesses, utilisée par Huygens et tous ses successeurs lors d'un changement de référentiel, ne découle pas du principe de relativité de Galilée. Cette règle d'additivité sera remise en cause par Einstein, lors de l'invention de la relativité restreinte.
L’absolu et le relatif de Newton
Newton, lecteur assidu de Descartes et de Galilée, en prolonge les observations quantitatives et amplifie la mathématisation de la physique, et place la loi d'inertie comme sa première loi de la physique, en y définissant au passage la notion de force.
Cette loi de l'inertie (en l'absence de force appliquée au corps, son accélération est nulle) n'est valable que dans certains repères (les repères galiléens), et Newton en introduisant les termes « absolu » et « relatif » pour qualifier les mouvements (qui pour lui prennent le sens de « vrai » et « apparent »), privilégie un repère galiléen particulier, « l'espace absolu », qui est le bon repère où on détermine le « mouvement absolu » des corps (et où il n'y a pas de force centrifuge ou autre force imputable au choix du référentiel). Les autres repères galiléens étant considérés comme des espaces relatifs privilégiés par rapport à ceux qui ne sont pas galiléens.
Ces considérations resteront admises jusqu'à Einstein, l'observateur pouvant toujours (semblait-il) détecter s'il est ou non dans un repère galiléen (en expérimentant la loi de l'inertie) et effectuer mathématiquement le changement de repère nécessaire, même si « l'espace absolu » restera toujours difficile à déterminer comme le regrettait déjà Newton.
Remarquons que, pour des raisons philosophiques, Leibniz a toujours lutté contre la notion d'espace et de temps absolu, sans réussir à influencer les sciences physiques. Dans une lettre à Samuel Clarke, adjoint de Newton, Leibniz tente de démontrer que la notion d'espace absolu est incompatible avec son principe de la raison suffisante.
Extrait de la troisième lettre de Leibniz à Clarke du 25 février 1716« Pour réfuter l'idée de ceux qui prennent l'Espace pour une substance, ou du moins pour quelque être absolu, j'ai plusieurs démonstrations, mais je ne veux me servir à présent que de celle dont on me fournit ici l'occasion.
Je dis donc que si l'Espace était un être absolu, il arriverait quelque chose dont il serait impossible qu'il y eut une raison suffisante, ce qui est contre notre Axiome. Voici comment je le prouve.
L'Espace est quelque chose d'absolument uniforme, et en l'absence des choses y placées, un point de l'Espace ne diffère absolument en rien d'un autre point de l'Espace.
Or, il suit de cela, à supposer que l'espace soit quelque chose en lui-même indépendamment de l'ordre des corps entre eux, qu'il est impossible qu'il existe une raison pour laquelle Dieu, gardant les mêmes situations des corps entre eux, a placé ainsi les corps dans l'espace et non autrement; et pour laquelle tout n'a pas été mis à rebours (par exemple) par échange de la droite et de la gauche.
Mais si l'Espace n'est autre chose que cet ordre ou rapport, et n'est rien du tout sans les corps, si ce n'est la possibilité d'en mettre; ces deux états, l'un tel qu'il est, l'autre supposé à rebours, ne diffèreraient aucunement entre eux. Leur différence ne se trouve que dans notre supposition chimérique : la réalité de l'espace en lui-même.
Mais dans la réalité, l'un sera en tout point la même chose que l'autre, puisqu'ils sont absolument indiscernables. Et par conséquent il n'y a pas lieu de demander la raison de la préférence de l'un à l'autre. »
L'influence majeure de Newton et la notion d'espace absolu firent que, pendant le XVIIIe siècle, le développement de la mécanique porta davantage sur les conséquences mathématiques de l'analyse dynamique du mouvement, plutôt que sur l'étude des repères en mouvement ou des changements de référentiels. Clairaut aborda certes cette dernière question en 1742, avec l'introduction de forces d'inertie d'entraînement, mais de manière imparfaite. La solution complète à la question du changement de référentiels fut apportée par Coriolis à partir de 1832. En 1833, Ferdinand Reich mit en évidence la déviation vers l'est d'un corps en chute libre, résultant du fait qu'un référentiel lié à la Terre n'est pas inertiel. Les forces d'inertie d'entraînement et de Coriolis permirent également d'expliquer l'expérience du pendule de Foucault, réalisée en 1851.
Son utilisation comme principe par Einstein dans la relativité restreinte
Il revient à Poincaré d'avoir désacralisé le choix de Newton dans son livre La Science et l'Hypothèse (1902) : il rejette « l'espace absolu » de Newton en montrant qu'il n'est nullement nécessaire à la physique, et constate même que la notion de référentiel galiléen et de mouvement rectiligne uniforme se définissent l'un par rapport à l'autre, et que la notion de ligne droite n'est pas une réalité mais une interprétation toute mathématique des expériences. Ainsi, il énonce la relativité de Galilée comme un Principe issu de l'expérience mais l'interprétant.
Einstein, lecteur de Poincaré, cherche à concilier le principe de relativité de Galilée (formulé : les lois sont les mêmes dans tous les référentiels galiléens) et le fait que la vitesse de la lumière est la même dans tous les référentiels galiléens (c'est un résultat de la théorie de l'électromagnétisme de Maxwell, interprété bien différemment jusque là avec « l'espace absolu » de Newton et l'éther). Sa conclusion est la relativité restreinte, publiée en 1905.
L'ancien professeur de mathématiques d'Einstein, Hermann Minkowski réinterprétera cette théorie dans le cadre d'un espace plat de dimension 4 ayant une mesure des distances particulière et où le principe de relativité de Galilée s'applique : l'espace-temps de Minkowski.
Sa généralisation par Einstein pour la relativité générale
Soucieux de cohérence intellectuelle, Einstein ne conçoit pas que la science privilégie des référentiels par rapport à d'autres : les lois de la physique changeraient-elles pour une même expérience suivant qu'elle est observée depuis un référentiel galiléen ou d'un référentiel non galiléen ? Il cherche donc une théorie généralisant le principe de Galilée à tous les référentiels, et aussi une loi de la gravitation compatible, autre objectif d'envergure.
Par sa découverte du principe d'équivalence, la gravitation devient (localement) un effet équivalent au choix d'un référentiel accéléré : la généralisation du principe de relativité, sous forme d'équations différentielles, suffira donc.
Imaginant un disque en rotation autour de son centre, il comprend que, d'après la relativité restreinte, une personne placée au centre et tournant avec verrait le rayon du disque inchangé mais son périmètre diminué : cela ne correspond pas à la géométrie euclidienne. La solution de son problème devait donc passer par la géométrie différentielle (qui englobe les géométries euclidiennes et non euclidiennes) et le calcul tensoriel qui va avec, et que, par bonheur, son ami Marcel Grossmann avait étudié dans le cadre de son doctorat.
Le calcul tensoriel est l'outil permettant d'établir des égalités vraies quel que soit le référentiel utilisé. Le principe de relativité ainsi généralisé porte aussi le nom de « principe de covariance générale ».
Après tâtonnements et hésitations face à cet outillage mathématique assez lourd, Einstein finit sa « théorie de la relativité générale » en 1915.
Références
- ↑ Lev Landau et Evguéni Lifchitz, Physique théorique, tome 2 : Théorie des champs, éd. MIR, Moscou [détail des éditions], §1.
- ↑ Lev Landau et Evguéni Lifchitz, Physique théorique, tome 2 : Théorie des champs, éd. MIR, Moscou [détail des éditions], §82.
- ↑ Albert Einstein, La Théorie de la relativité restreinte et généralisée, Gaulthier-Villards, 1921, traduit par Mlle J. Rouvière et préfacé par Émile Borel ; chapitre XVIII.
- ↑ Jean-Claude Boudenot ; Électromagnétisme et gravitation relativistes, ellipse (1989), (ISBN 2729889361), chapitre II, §3.
- ↑ Galilée, Dialogo supra i due massimi sistemi del Mondo, 1632, réédité chez Edizione nazionale sotto gli auspicii di sua maesta il re d'Italia. Vol. VII, p.142. Édition française : Dialogue sur les deux grands systèmes du Monde, Seuil (1992), p.141, traduction de René Fréreux avec le concours de François de Gandt
- ↑ Galilée, Dialogo supra i due massimi sistemi del Mondo, 1632, réédité chez Edizione nazionale sotto gli auspicii di sua maesta il re d'Italia. Vol. VII, p.213. Édition française : Dialogue sur les deux grands systèmes du Monde, Seuil (1992), p.204, traduction de René Fréreux avec le concours de François de Gandt
- ↑ Il le dit dans son « Dialogue... »[réf. nécessaire](sans utiliser le mot inertiel qui n'est pas de son époque). Faut-il y voir un reste de l'influence de la doctrine aristotélicienne comme le suggère F. Balibar dans son livre Galilée, Newton lus par Einstein ?
- ↑ Oeuvres complètes de Huygens, tome XVI, éditées par la Société Hollandaise des Sciences (qui souligne dans l'introduction l'originalité de la démarche de l'auteur), (1929)
Notes
- ↑ et exprime le caractère absolu du temps en physique classique.
- ↑ Cette égalité a été considérée comme une évidence due à la géométrie euclidienne, jusqu'au travaux de Lorentz, d'Henri Poincaré et d'Albert Einstein
- ↑ Le temps, les longueurs, les vitesses (mis à part la vitesse de la lumière) et les accélérations sont relatifs au référentiel (supposé inertiel) de l'observateur qui mesure.
Bibliographie
- Françoise Balibar, Galilée, Newton lus par Einstein, PUF, 1984
- Albert Einstein, La Théorie de la relativité restreinte et généralisée, Gaulthier-Villards, 1921, traduit par Mlle J. Rouvière et préfacé par M. Émile Borel.
- Banesh Hoffmann (avec la collaboration de Helen Dukas), Albert Einstein, créateur et rebelle, 1975, Éditions du Seuil, coll. Points Sciences, trad. de l'américain par Maurice Manly. (ISBN 2-02-005347-0)
- Lev Landau et Evguéni Lifchitz, Physique théorique, éd. MIR, Moscou [détail des éditions]
- James H. Smith, Introduction à la relativité , 1965; pour la France : Masson éditeur, traduction depuis l'américain par Philippe Brenier en 1997, préface de Jean-Marc Lévy-Leblond. (ISBN 2-225-82985-3)
Articles connexes
- Référentiel galiléen
- Relativité d'échelle
- Relativité galiléenne
- Relativité générale
- Relativité restreinte
- Vitesse relative
Liens externes
- Catégorie Relativité de l’annuaire dmoz
- Poincaré et le principe de relativité par Michel Paty, 1994
- Une vidéo pratique sur la théorie de la relativité
- Vidéoconférence sur le thème "La Relativité générale" (intervention de Thibault Damour)
- Portail de la physique
Catégories : Relativité | Principe physique
Wikimedia Foundation. 2010.