Fusion Nucléaire

Le Soleil, siège de nombreuses réactions de fusion nucléaire.

La fusion nucléaire (dite parfois thermonucléaire) est, avec la fission, l’un des deux principaux types de réactions nucléaires appliquées. Il ne faut pas confondre la fusion nucléaire avec la fusion du cœur d’un réacteur nucléaire, qui est un accident nucléaire particulièrement redoutable.

La fusion nucléaire est un processus où deux noyaux atomiques s’assemblent pour former un noyau plus lourd. La fusion de noyaux légers dégage d’énormes quantités d’énergie provenant de l’attraction entre les nucléons due à l’interaction forte (voir Énergie de liaison atomique).

Cette réaction est à l’œuvre de manière naturelle dans le Soleil et la plupart des étoiles de notre univers. En dépit des travaux de recherche réalisés dans le monde entier depuis les années 1950, aucune application industrielle de la fusion à la production d’énergie n’a encore abouti, en dehors du domaine militaire avec la bombe H, étant donné que cette application ne vise aucunement à contenir et maîtriser la réaction produite. Il en existe cependant quelques autres usages moins médiatisés, comme les générateurs de neutrons utilisés notamment pour la détection des explosifs^[1].

Un intérêt de la fusion nucléaire est de pouvoir produire théoriquement beaucoup plus d’énergie (de 3 à 4 fois plus), à masse de « combustible » égale, que la fission. De plus, les océans contiennent naturellement suffisamment de deutérium pour permettre d’alimenter en énergie la planète pendant quelques centaines de millénaires.

Contrairement à la fission nucléaire, les produits de la fusion eux-mêmes (principalement de l’hélium 4) ne sont pas radioactifs, mais lorsque la réaction utilisée émet des neutrons rapides, ces derniers peuvent en revanche transformer les noyaux qui les capturent en isotopes pouvant l’être.

Mécanisme de la fusion

Fusion nucléaire.

Une réaction de fusion nucléaire nécessite que deux noyaux atomiques s’interpénètrent. Il faut pour cela que les noyaux surmontent la répulsion due à leurs charges électriques toutes deux positives (phénomène dit de barrière coulombienne). Si l’on appliquait uniquement les lois de la mécanique classique, la probabilité d’obtenir la fusion des noyaux serait très faible, en raison de l’énergie cinétique (correspondant à l’agitation thermique) extrêmement élevée nécessaire au franchissement de la barrière. Cependant, la mécanique quantique prévoit, ce qui se vérifie en pratique, que la barrière coulombienne peut également être franchie par effet tunnel, à des énergies plus faibles.

Les énergies nécessaires à la fusion restent très élevées, correspondant à des températures de plusieurs dizaines ou même centaines de millions de degrés selon la nature des noyaux (voir plus bas : Plasmas de fusion). Au sein du Soleil par exemple, la fusion de l’hydrogène, qui aboutit, par étapes, à produire de l’hélium s’effectue à des températures de l’ordre de 15 millions de kelvins, mais suivant des schémas de réaction différents de ceux étudiés pour la production d’énergie de fusion sur Terre. Dans certaines étoiles plus massives, des températures plus élevées permettent la fusion de noyaux plus lourds.

Lorsque de petits noyaux fusionnent, le noyau résultant se retrouve dans un état instable et doit revenir à un état stable d’énergie plus faible, en éjectant une ou plusieurs particules (photon, neutron, proton, noyau d’hélium, selon le type de réaction), l’énergie excédentaire se répartit entre le noyau et les particules émises, sous forme d’énergie cinétique. Pour que la fusion soit énergétiquement rentable, il est nécessaire que l’énergie produite soit supérieure à l’énergie consommée pour l’entretien des réactions et par pertes thermiques vers le milieu extérieur. Dans les réacteurs à fusion, il faut ainsi éviter tout contact entre le milieu de réaction et les matériaux de l’environnement, ce que l’on réalise par un confinement immatériel.

Dans les cas où aucun état à peu près stable n’existe, il peut être impossible de provoquer la fusion de deux noyaux (exemple : ⁴He + ⁴He).

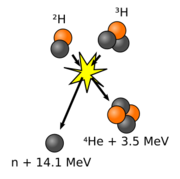
Les réactions de fusion qui dégagent le plus d’énergie sont celles qui impliquent les noyaux les plus légers. Ainsi les noyaux de deutérium (un proton et un neutron) et de tritium (un proton et deux neutrons) sont impliqués dans les réactions suivantes :

• deutérium + deutérium → (hélium 3 + 0,82 MeV) + (neutron + 2,45 MeV)
• deutérium + deutérium → (tritium + 1,01 MeV) + (proton + 3,03 MeV)
• deutérium + tritium → (hélium 4 + 3,52 MeV) + (neutron + 14,06 MeV)
• deutérium + hélium 3 → (hélium 4 + 3,67 MeV) + (proton + 14,67 MeV)

Ce sont ces réactions qui sont les plus étudiées en laboratoire lors d’expériences de fusion contrôlée.

La fusion contrôlée

Si la fission est contrôlée depuis longtemps pour la production d'électricité, ce n'est pas encore le cas de la fusion.

Cette réaction est difficile à réaliser car il faut rapprocher deux noyaux qui ont tendance naturellement à se repousser. Maîtriser sur Terre la fusion de noyaux légers, tels que le deutérium et le tritium, ouvrirait la voie à des ressources en énergie quasiment illimitées.

Grâce aux machines appelées « tokamak », les chercheurs expérimentent depuis plusieurs années la fusion par confinement magnétique. Aujourd'hui la communauté scientifique internationale s'apprête, en France à Cadarache, à construire le plus important tokamak jamais réalisé. C'est le projet ITER qui devrait permettre de démontrer la faisabilité scientifique et technologique de l'énergie de fusion.

Procédés

Il existe différents procédés concevables permettant d’arriver à confiner le milieu de réaction pour produire des réactions de fusion nucléaire, notamment la fusion par confinement magnétique et la fusion par confinement inertiel. Aucun d’entre eux n’a encore abouti à des résultats industriels pour la production d’énergie électrique.

Fusion par confinement magnétique

Les configurations fermées

Dans ces configurations, les lignes de champ magnétique confinent efficacement les particules.

• les tokamaks, où l’on confine un mélange gazeux d’isotopes d’hydrogène grâce à un champ magnétique produit par des bobines et un courant induit circulant dans le plasma (exemples : Tore Supra, ITER) ;
• les stellarators, où le confinement est entièrement assuré par les bobines (exemple : Wendelstein 7-X) ;
• les sphéromaks de forme sphérique ;

Les configurations ouvertes

• les machines à piège à miroirs magnétiques, qui pourraient aussi être utilisées pour la propulsion spatiale.

Le chauffage dans la fusion par confinement magnétique

Divers moyens sont à la disposition des physiciens de la fusion pour chauffer le plasma de deutérium et de tritium.

Un premier moyen est constitué par un système permettant d’engendrer un intense courant électrique au sein du plasma. Dans la mesure où des électrodes pollueraient le plasma, les chercheurs induisent ce courant grâce à un champ magnétique variable, soit croissant, soit décroissant. Ainsi, le courant induit possède des limites.

Il est aussi possible de chauffer le plasma au moyen d’un faisceau d’atomes neutres. Ces derniers sont, dans un dispositif distinct, ionisés pour pouvoir être accélérés par un champ électrique. Par la suite et avant d’être injectés dans le plasma, ils sont neutralisés. Des atomes neutres sont nécessaire puisque des ions seraient déviées par le champ de confinement et ne seraient pas en mesure d’accéder au centre du plasma. Une fois au centre de ce dernier, les atomes neutres s’ionisent et, du fait de leur excédent d’énergie par rapport à l’énergie cinétique moyenne du tritium et du deutérium, cédent une partie de leur énergie cinétique au milieu de par des collisions. Ces atomes neutres ne sont autres que des atomes de tritium et de deutérium. Il assure donc aussi l’approvisionnement en combustible.

Fusion par confinement inertiel

Dans cette voie, l'énergie est apportée par un faisceau de lumière laser ou bien par un faisceau de particules chargées (électrons ou ions) à une bille de combustible de quelques millimètres de diamètre. L'ionisation et le chauffage rapide de la paroi externe de la cible conduit à une expansion du plasma, à une vitesse égale à environ c/1000, c désignant la vitesse de la lumière dans le vide, soit environ 3 10⁸ m/s. Il s'en suit l'apparition d'une onde de choc centripète, qui va concentrer le combustible deutérium-tritium au centre de la cible, dans un diamètre environ 10 fois plus faible que le diamètre initial. On parle d'effet fusée pour qualifier cette convergence de la masse de la cible opposée à l'expansion du plasma périphérique (principe des actions réciproques de la troisième loi de Newton). Cette compression conduit à la fois à densifier le milieu combustible, pour donner une densité nulle part accessible sur terre, à savoir 10²⁶ cm^-3, et une température de 10 millions de degrés. Ces conditions conduisent à un nombre très important de réactions de fusion, pendant environ 10 picosecondes.

• les machines à Confinement inertiel par laser, où une microbille de deutérium-tritium enfermée dans une coquille de plastique est éclairée par de puissants lasers dont la puissance dépasse 1 pétawatt (exemple : laser Mégajoule, NIF) ; un gain de 10 entre l'énergie de fusion et l'énergie apportée par laser (environ 1.8 MJ) est attendu dans les expériences qui commenceront dans les années 2010.
• les machines à striction axiale (ou Z-pinch), où une pastille d’isotopes est comprimée par des impulsions de rayons X (exemple : Z machine (plus de 2 milliards de degrés atteints !) des Laboratoires Sandia). Les conditions de fusion ont été obtenues en mars 2006 dans une (en) Z machine à confinement axial. Les travaux ont commencé sur la conception d’un réacteur expérimental à impulsion utilisant ce principe.

Plasmas de fusion

À la température à laquelle la fusion est susceptible de se produire, la matière est à l’état de plasma.

Il s’agit d’un état particulier de la matière première dans lequel les atomes ou les molécules forment un gaz ionisé.

Un ou plusieurs électrons du nuage électronique qui entoure chaque noyau ont été arrachés, laissant des ions chargés positivement et des électrons libres, l’ensemble étant électriquement neutre.

Dans un plasma thermique, la grande agitation des ions et des électrons produit de nombreuses collisions entre les particules. Pour que ces collisions soient suffisamment violentes et entrainent une fusion, trois grandeurs interviennent :

1. la température T ;
2. la densité N ;
3. le temps de confinement τ.

Le critère de Lawson établit que le facteur Nτ doit atteindre un certain seuil pour obtenir le breakeven où l’énergie libérée par la fusion est égale à l’énergie dépensée. L’ignition se produit ensuite à un stade beaucoup plus élevé de production d’énergie (impossible à créer dans les réacteurs actuels). Il s’agit du seuil à partir duquel la réaction est capable de s’auto-entretenir. Pour la réaction deutérium + tritium, ce seuil est de 10¹⁴ s/cm³.

Analyse de la réaction deutérium + tritium

L’énergie de liaison des constituants provient de la force d’interaction nucléaire forte, l’une des quatre forces d’interaction fondamentales de l’Univers.

Or l’investissement énergétique à fournir pour obtenir cette liaison est proportionnel au produit des charges électriques des deux noyaux en présence. C’est pourquoi le choix pour la fusion s’est porté sur le deutérium et le tritium, deux isotopes lourds de l’hydrogène, pour lesquels ce produit vaut 1.

L’énergie minimale à fournir pour obtenir une fusion est de 4 keV (équivalent à une température de 40 millions de kelvin) ; l’énergie libérée est alors de 17,6 MeV répartie pour 80 % dans le neutron émis et pour 20 % dans l’hélium 4 produit.

Mais l’énergie nécessaire pour atteindre le critère de Lawson et un rendement suffisamment positif se situe vers 10 keV soit 100 millions de degrés.

La réaction « deutérium + tritium » se traduit par une émission de neutrons rapides. Ces neutrons sont impossibles à confiner électromagnétiquement car ils ont une charge électrique nulle. Ils sont donc susceptibles d’être capturés par les noyaux d’atomes de la paroi de l’enceinte, qu’ils transmutent parfois en isotopes radioactifs (phénomène d’activation). L’activation peut s’accompagner de production de noyaux d’hélium, susceptibles de fragiliser les matériaux de structure. Elle pourrait compliquer l’usage industriel de la fusion, et fait l’objet d’études avec différentes propositions de solutions (par exemple parois en composites, ou encore alliages spécifiques de fer), mais elles nécessitent des études expérimentales difficiles à réaliser à court terme. Les réactions générant des neutrons ne sont donc pas totalement « propres », mais sont toutefois nettement moins génératrices de déchets que les réactions de fission nucléaire, et la durée de vie de ces déchets est bien inférieure à celle des produits radioactifs créés dans les centrales à fission nucléaire.

Si le deutérium est disponible naturellement en grandes quantités dans les océans, il nécessite la mise en place de méthodes très complexes pour en être extrait, le tritium doit être préparé artificiellement car il ne se trouve qu’en très petite quantité dans le milieu naturel de par sa nature d’isotope radioactif à courte durée de demi-vie (la moitié disparait en 12,3 ans).

Applications

Si la fusion a pu être utilisée dans le domaine militaire avec les bombes H, il n’existe pas encore d’application civile de la fusion pour la production d’électricité. Seuls des prototypes d’étude ont pu être construits actuellement.

Les réactions de fusion importantes

Chaines de réactions en astrophysique

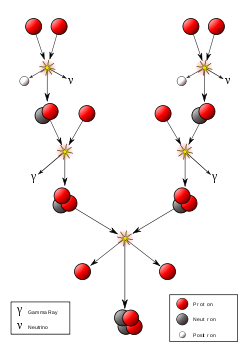La chaîne proton-proton prédomine dans les étoiles d’une taille similaire ou inférieure à celle du Soleil.

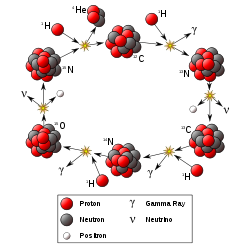Le cycle carbone-azote-oxygène prédomine dans les étoiles de masse supérieure à celle du Soleil.

Le processus de fusion le plus important dans la nature est celui qui alimente les étoiles. Le résultat net est la fusion de quatre protons en une particule alpha (noyau d’hélium 4), accompagnée de la libération de deux positrons, de deux neutrinos (qui transforment deux des protons en neutrons) et d’énergie, mais diverses réactions individuelles sont impliquées selon la masse de l’étoile. Dans les étoiles de taille similaire ou inférieure à celle du Soleil, la chaîne proton-proton prédomine. Dans les étoiles plus lourdes, le cycle carbone-azote-oxygène (CNO) est le plus important. Les deux types de processus sont à l’origine de la création de nouveaux éléments dans le cadre de la nucléosynthèse stellaire.

Aux températures et densités du cœur des étoiles, le taux de réaction de fusion est notoirement peu élevé. Par exemple, à la température (T ≈ 15 MK) et à la densité (160 g/cm³) du cœur du Soleil, le taux de libération d’énergie est seulement de 276 μW/cm³ - environ le quart du débit de chaleur par unité de volume d’un homme au repos^[2]. Ainsi, la reproduction en laboratoire des conditions du cœur des étoiles à des fins de production d’énergie de fusion est totalement impossible à mettre en pratique. Les taux de réaction dépendant fortement de la température (exp(−E/kT)), il est nécessaire, pour atteindre des taux raisonnables de production d’énergie dans des réacteurs à fusion nucléaire, de travailler à des températures 10 à 100 fois plus élevées que celles du cœur des étoiles, soit T ≈ 0,1 — 1 GK (de l’ordre de 100 millions à un milliard de kelvins.)

Critères et candidats pour les réactions terrestres

Dans la fusion mise en œuvre par l’homme, rien n’impose que le combustible utilisé soit constitué de protons, et il est possible d’employer des températures plus élevées pour accéder à des réactions de plus grande section efficace. Cela implique une valeur plus faible du critère de Lawson, et donc moins d’efforts à produire pour le démarrage des réactions. La production de neutrons, qui constitue un sujet de préoccupation car elle entraine une activation radiologique de la structure du réacteur, possède en contrepartie l’avantage d’autoriser l’extraction de l’énergie de fusion ainsi que la production de tritium. Les réactions qui ne produisent pas de neutrons sont dites aneutroniques.

Pour être utilisable comme source d’énergie, une réaction de fusion doit satisfaire à plusieurs critères. Elle doit :

• être exothermique : Cette condition semble évidente, mais elle limite les réactifs à la partie de la courbe des énergies de liaison correspondant aux faibles numéros atomiques Z (nombre de protons). Elle fait également de l’hélium ⁴He le produit le plus fréquent en raison de ses liaisons extrêmement étroites, bien que l’on rencontre également ³He et ³H ;
• impliquer des noyaux à Z faible : La répulsion électrostatique doit être vaincue pour que les noyaux puissent se rapprocher suffisamment pour fusionner ;
• avoir deux réactifs : À toutes les densités inférieures à celles des étoiles, la collision simultanée de trois particules est par trop improbable. Dans le cas du confinement inertiel, on dépasse à la fois les densités et les températures stellaires, ce qui permet de compenser la faiblesse du troisième paramètre du critère de Lawson, la très brève durée de confinement ;
• avoir deux produits ou plus : Ceci permet la conservation simultanée de l’énergie et de l’impulsion ;
• conserver à la fois les protons et les neutrons : Les sections efficaces pour l’interaction faible sont trop petites.

Peu de réactions satisfont tous ces critères. Les suivantes sont celles dont les sections efficaces sont les plus grandes^{[réf. nécessaire]} :

(1)

2D

+

3T

→

4He

(

3,5 MeV

)

+

n0

(

14,1 MeV

)

(2i)

2D

+

2D

→

3T

(

1,01 MeV

)

+

p+

(

3,02 MeV

)

50%

(2ii)

→

3He

(

0,82 MeV

)

+

n0

(

2,45 MeV

)

50%

(3)

2D

+

3He

→

4He

(

3,6 MeV

)

+

p+

(

14,7 MeV

)

(4)

3T

+

3T

→

4He

+

2 n0

+

11,3 MeV

(5)

3He

+

3He

→

4He

+

2 p+

+

12,9 MeV

(6i)

3He

+

3T

→

4He

+

p+

+

n0

+

12,1 MeV

51%

(6ii)

→

4He

(

4,8 MeV

)

+

2D

(

9,5 MeV

)

43%

(6iii)

→

4He

(

0,5 MeV

)

+

n0

(

1,9 MeV

)

+

p+

(

11,9 MeV

)

6%

(7i)

2D

+

6Li

→

2 4He

+

22,4 MeV

(7ii)

→

3He

+

4He

+

n0

+

2,56 MeV

(7iii)

→

7Li

+

p+

+

5,0 MeV

(7iv)

→

7Be

+

n0

+

3,4 MeV

(8)

p+

+

6Li

→

4He

(

1,7 MeV

)

+

3He

(

2,3 MeV

)

(9)

3He

+

6Li

→

2 4He

+

p+

+

16,9 MeV

(10)

p+

+

11B

→

3 4He

+

8,7 MeV

Pour les réactions avec deux produits, l’énergie est répartie entre eux en proportion inverse de leurs masses, comme indiqué. Dans la plupart des réactions avec trois produits, la distribution des énergies est variable. Pour les réactions qui peuvent donner naissance à plus d’un ensemble de produits, les proportions sont indiquées. Certaines réactions candidates peuvent être éliminées immédiatement^[3]. La réaction D-⁶Li ne présente aucun avantage par rapport à p-¹¹B car, si elle est pratiquement aussi difficile à déclencher, elle produit considérablement plus de neutrons à travers des réactions ²D-²D annexes. Il existe également une réaction p-⁷Li, cependant sa section efficace est bien trop faible, sauf peut-être quand T_i > 1 MeV, mais à de telles températures une réaction endothermique, produisant directement des neutrons, devient très significative. Il existe enfin une réaction p-⁹Be, qui non seulement est difficile à déclencher, mais dans laquelle ⁹Be peut être aisément amené à se scinder en deux alphas et un neutron.

Outre les réactions de fusion, les réactions suivantes impliquant des neutrons sont importantes pour la production de tritium dans les bombes à fusion « sèches » et certains réacteurs en projet :

n0	+	6Li	→	3T	+	4He
n0	+	7Li	→	3T	+	4He	+	n0

Pour évaluer l’utilité de ces réactions, outre les réactifs, les produits, et l’énergie libérée, on doit aussi disposer d’informations sur la section efficace. Tout dispositif de fusion possède une pression maximale qu’il est capable de maintenir, et un dispositif économique devra toujours travailler à proximité de ce maximum. Cette pression étant donnée, l’énergie de fusion maximale est obtenue en choisissant une température telle que <σv>/T² soit maximal. C’est aussi la température à laquelle la valeur du triple produit nTτ requise pour l’ignition est minimale, cette dernière étant inversement proportionnelle à <σv>/T² (voir critère de Lawson). Cette température optimale ainsi que la valeur de <σv>/T² à cette température sont données pour quelques-unes de ces réactions dans la table suivante.

Nombre de ces réactions forment des chaines. Par exemple, un réacteur alimenté en ³T et ³He crée un peu de ²D, qu’il est alors possible d’utiliser dans la réaction ²D + ³He si les énergies sont « correctes ». Une idée élégante consiste à combiner les réactions (8) et (9). ³He produit par la réaction (8) est susceptible de réagir avec ⁶Li produit par la réaction (9), avant sa thermalisation complète. On produit ainsi un proton qui à son tour peut subir la réaction (8) avant thermalisation. Une analyse détaillée montre que cette idée ne fonctionnera en fait pas très bien, mais c’est un bon exemple d’un cas où l’hypothèse habituelle d’un plasma maxwellien n’est pas appropriée.

Neutronicité, exigences en confinement et densité de puissance

Les seules réactions de fusion produites jusqu’à présent par l’homme qui aient atteint l’ignition sont celles qui ont été créées dans les bombes à hydrogène ; on voit ici l’explosion d’Ivy Mike, premier essai d’une telle bombe.

N’importe laquelle des réactions ci-dessus peut en principe être à la base de la production d’énergie de fusion. Outre la température et la section efficace abordées plus haut, il est nécessaire d'examiner l’énergie totale des produits de fusion E_fus, l’énergie des produits de fusion électriquement chargés E_ch, et le numéro atomique Z des réactifs autres que les isotopes de l’hydrogène.

Cependant, la spécification de la réaction ²D-²D entraine certaines difficultés. Tout d’abord, il faut effectuer une moyenne sur les deux branches (2i) et (2ii). Il faut ensuite, ce qui est plus difficile, décider comment traiter les produits ³T et ³He. ³T « brule » si bien dans un plasma de deutérium qu’il est pratiquement impossible de l’en extraire. La réaction ²D-³He est optimale à une température bien plus élevée, et la combustion à la température optimale pour ²D-²D peut être faible ; il semble donc raisonnable de supposer que ³T va brûler, mais pas ³He, et que l’énergie ainsi libérée va s’ajouter à celle de la réaction. L’énergie de fusion ²D-²D sera donc E_fus = (4,03+17,6+3,27)/2 = 12,5 MeV, et celle des particules chargées E_ch = (4,03+3,5+0,82)/2 = 4,2 MeV.

Un autre aspect spécifique de la réaction ²D-²D tient à la présence d’un seul réactif, ce que l’on doit prendre en compte lors du calcul du taux de réaction.

En se basant sur ces choix, les paramètres de quatre des réactions les plus importantes sont présentés dans la table suivante :

La dernière colonne correspond à la neutronicité de la réaction, définie comme la fraction de l’énergie de fusion libérée sous forme de neutrons. C’est un indicateur important de l’ampleur des problèmes associés aux neutrons, tels que les dommages provoqués par les radiations, la protection biologique, la télémanipulation et la sécurité. Pour les deux premières réactions, elle est donnée par (E_fus-E_ch)/E_fus. Pour les deux dernières, où cette formule donnerait un résultat égal à 0, les valeurs indiquées sont des estimations grossières basées sur des réactions annexes qui produisent des neutrons dans un plasma en équilibre thermique.

Bien entendu, il est nécessaire de mélanger les réactifs dans les proportions optimales. C’est le cas lorsque chaque ion de réactif et ses électrons associés participent pour moitié à la pression. En supposant que la pression totale est fixée, cela signifie que la densité des ions non hydrogène est plus faible que celle des ions hydrogène d’un facteur 2/(Z+1). En conséquence le taux de ces réactions est réduit du même facteur, ce qui constitue la différence la plus importante dans les valeurs de <σv>/T². D’autre part, comme la réaction ²D-²D n’a qu’un seul réactif, le taux est deux fois plus élevé que si le combustible était constitué de deux isotopes d’hydrogène.

Il existe donc une « pénalité » de (2/(Z+1)) pour les combustibles autres que l’hydrogène, provenant du fait qu’ils ont besoin de plus d’électrons, ce qui absorbe de la pression sans participer à la réaction de fusion. Il est généralement correct de supposer que la température électronique et la température ionique sont pratiquement égales. Certains auteurs envisagent que les électrons puissent être maintenus à une température nettement inférieure à celle des ions. Dans de telles situations, connues sous le nom de « modes à ions chauds », la « pénalité » ne s'appliquerait pas. Il existe de la même façon un « bonus » d’un facteur 2 pour la réaction ²D-²D dû au fait que chaque ion peut réagir avec n’importe lequel des autres ions, et pas seulement avec une fraction d’entre eux.

La table suivante permet de comparer ces réactions.

La valeur maximale de <σv>/T² est reprise d’une table précédente. Le facteur « pénalité/bonus » est celui lié, soit à un réactif non hydrogène, soit à une réaction sur une espèce unique. Les valeurs de la colonne « réactivité » sont obtenues en divisant 1,24×10^-24 par le produit des deuxième et troisième colonnes ; chaque valeur indique le facteur de ralentissement des réactions par rapport à la réaction ²D-³T dans des conditions comparables. La colonne « critère de Lawson » pondère ces résultats par E_ch et donne une indication de la difficulté d’atteindre l’ignition avec ces réactions, par rapport à la réaction ²D-³T. La dernière colonne, étiquetée « densité de puissance », pondère la réactivité pratique par E_fus ; elle donne le facteur de réduction de la densité de puissance de fusion pour une réaction particulière par rapport à la réaction ²D-³T, et peut être considérée comme une mesure du potentiel économique.

Pertes par Bremsstrahlung dans les plasmas quasi-neutres isotropes

Les ions subissant la fusion ne le font quasiment jamais de façon isolée, mais sont mélangés à des électrons qui neutralisent la charge électrique des ions en formant un plasma. Les électrons ayant généralement une température comparable ou supérieure à celle des ions, ils entrent en collision avec ceux-ci et émettent des rayons X dont l'énergie est de l'ordre de 10 à 30 keV (Bremsstrahlung ou rayonnement de freinage). Le Soleil et les étoiles sont opaques aux rayons X, mais la plupart des réacteurs de fusion terrestre ont une épaisseur optique faible pour les X de cette gamme d'énergie. La réflexion des rayons X est difficile à obtenir, mais ils sont absorbés (et convertis en chaleur) par une épaisseur de moins d'un mm d'acier inoxydable (qui fait partie du blindage d'un réacteur). Le rapport entre la puissance de fusion produite et ces pertes est un critère de qualité important de la réaction. La valeur maximale de ce rapport est généralement obtenue à une température bien plus élevée que celle qui rend la densité de puissance maximale (voir le sous-chapitre précédent). La table suivante montre la température optimale approximative ainsi que le rapport de puissance à cette température pour plusieurs réactions.

Il est probable que les véritables rapports entre puissance de fusion et puissance de Bremsstrahlung sont notablement plus faibles, et ce pour diverses raisons. En premier lieu, les calculs supposent que l’énergie des produits de fusion est entièrement transmise aux ions du combustible, qui la perdent ensuite par collision au profit des électrons, qui à leur tour perdent de l’énergie par Bremsstrahlung. Cependant, comme les produits de fusion ont une vitesse bien plus grande que les ions du combustible, ils abandonnent une partie significative de leur énergie directement aux électrons. En deuxième lieu, le plasma est supposé ne comporter que des ions de combustible. En pratique, il existe une proportion significative d’ions d’impuretés, qui vont faire diminuer le rapport. En particulier, les produits de fusion eux-mêmes doivent demeurer dans le plasma jusqu’à ce qu’ils aient abandonné leur énergie, et y resteront encore quelque temps, quel que soit le procédé de confinement envisagé. En dernier lieu, tous les canaux de perte d’énergie autres que le Bremsstrahlung ont été considérés comme négligeables. Les deux derniers facteurs sont apparentés. Sur les plans théorique et expérimental, le confinement des particules et le confinement de l’énergie semblent étroitement apparentés. Dans un procédé de confinement qui retient efficacement l’énergie, les produits de fusion vont s’accroître. Si les produits de fusion sont expulsés efficacement, alors le confinement énergétique sera médiocre.

Les températures pour lesquelles le rapport entre puissances de fusion et de Bremsstrahlung est maximal sont dans tous les cas plus élevées que celles pour lesquelles la densité de puissance est maximale et le triple produit de fusion minimal. Cela ne change pas beaucoup le point de fonctionnement optimal pour ²D-³T car la part de Bremsstrahlung est faible, mais cela pousse les autres combustibles vers des régimes où la densité de puissance relativement à ²D-³T est encore plus faible, et le confinement requis encore plus difficile à obtenir. Pour ²D-²D et ²D-³He, les pertes par Bremsstrahlung constituent un problème sérieux, peut-être même bloquant. Pour ³He-³He, p⁺-⁶Li et p⁺-¹¹B, les pertes par Bremsstrahlung paraissent rendre impossible la réalisation d’un réacteur à fusion utilisant ces combustibles avec un plasma quasi-neutre isotrope^[4]. Cette limitation ne s'applique ni aux plasmas non neutres, ni aux plasmas anisotropes^{[réf. nécessaire]}, qui ont cependant leurs propres défis à relever.

Formations universitaires

Après la décision prise en 2006 d'implanter le projet ITER en France, plusieurs institutions françaises d'enseignement supérieur se sont jointes de façon à ouvrir une spécialité de master "sciences de la fusion". ^[5] Cette formation vise à former les futurs scientifiques et ingénieurs, français ou étrangers, qui souhaitent s'investir dans les programmes tant nationaux que privés concernant les recherches sur l’énergie et la fusion, en particulier dans l'exploitation scientifique et technique de grands équipements associés. La formation se fait au travers de trois parcours : deux portent essentiellement sur la physique de la fusion, soit par confinement magnétique, soit par confinement inertiel ; un troisième parcours est à contenu plus technologique.

Dix établissements, répartis sur quatre sites du territoire français, sont cohabilités pour délivrer ce diplôme, avec des enseignements qui ont lieu en parallèle dans ces sites et lors de regroupement des étudiants à Cadarache et Bordeaux :

• Universités d'Aix-Marseille et INSTN en région PACA,
• Université Bordeaux 1 en Aquitaine,
• Université Nancy I, INPL en Lorraine
• Université Paris 6, Université Paris Sud 11, École polytechnique (ParisTech), INSTN pour l'Île de France.

Cinq écoles d'ingénieur sont également associées:

• l'École Centrale de Marseille,
• l'École Centrale Paris,
• Supelec,
• SupOptique (ParisTech),
• l'ENSAM (ParisTech).

Notes et références

Source

• (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Nuclear fusion ».

Voir aussi

Articles connexes

• Fusion par confinement magnétique
• Fusion par confinement inertiel
• Fusion aneutronique
• ITER (International Thermonuclear Experimental Reactor)
• Fusion froide
• Physique des plasmas

Bibliographie

• (en) Cornelius Marius Braams, Peter E. Stott, Nuclear Fusion, CRC Press, 2002 (ISBN 0-7503-0705-6)  (aperçu limité en ligne)
• (en) Stefano Atzeni, Jürgen Meyer-ter-Vehn, The Physics of Inertial Fusion: Beam Plasma Interaction, Hydrodynamics, Hot Dense Matter, Oxford University Press, 2004 (ISBN 0-19-856264-0)  (aperçu limité en ligne)

Liens externes

• (fr) SCK.CEN Centre d’étude de l’Énergie Nucléaire
• (fr) Fusion magnétique, dossier du CEA
• (en) Agence internationale pour l’énergie atomique

• Portail de la physique
• Portail de l’énergie
• Portail de l’astronomie