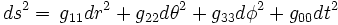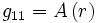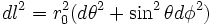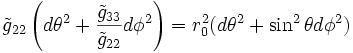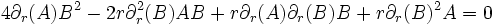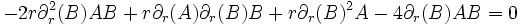- Metrique de Schwarzschild
-
Métrique de Schwarzschild
Pour consulter un article plus général, voir : Trou noir de Schwarzschild.En astrophysique, et plus précisément dans le cadre de la Relativité générale, la métrique de Schwarzschild est une métrique permettant de décrire le champ gravitationnel autour d'une masse sphérique et statique (ie qui n'est pas en rotation). Cette masse peut être une étoile, une planète ou un trou noir de Schwarzschild.
Sommaire
Conventions mathématiques
On utilise un système de coordonnées qui a pour coordonnées
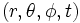 (désignant le rayon, l'angle azimutal, l'angle d'inclinaison ou d'altitude et le temps). Chacune de ces coordonnées peut être labélisée 1,2,3 et 0 respectivement pour simplifier. Le cas considéré par Karl Schwarzschild est celui d'un espace symétrique, sphérique, statique et vide. Plus précisément,
(désignant le rayon, l'angle azimutal, l'angle d'inclinaison ou d'altitude et le temps). Chacune de ces coordonnées peut être labélisée 1,2,3 et 0 respectivement pour simplifier. Le cas considéré par Karl Schwarzschild est celui d'un espace symétrique, sphérique, statique et vide. Plus précisément,- Un espace-temps avec symétrie sphérique, on dit aussi isotrope, est un espace-temps où toutes les composantes de la métrique sont inchangées lors d'une opération de rotation. Mathématiquement:
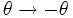 et d'une façon similaire
et d'une façon similaire 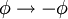 .
. - Un espace-temps statique est un espace-temps dans lequel les composantes de la métriques sont indépendants du temps, et où donc la géométrie de l'espace-temps reste inchangée pour l'opération de translation du temps. Mathématiquement:
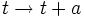 . Ce qui implique que
. Ce qui implique que  , où l'on a utilisé la convention
, où l'on a utilisé la convention 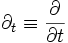 , qui permet de grandement simplifier l'écriture. De plus
, qui permet de grandement simplifier l'écriture. De plus 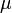 et
et 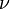 peuvent prendre les valeurs 1, 2, 3 ou 0 (ou respectivement
peuvent prendre les valeurs 1, 2, 3 ou 0 (ou respectivement  ).
). - Une solution dans le vide est une solution pour laquelle le tenseur énergie-impulsion de l'équation d'Einstein est nul:
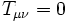 en dehors du corps central. Pour le cas d'une constante cosmologique nulle, cela implique que
en dehors du corps central. Pour le cas d'une constante cosmologique nulle, cela implique que  , où
, où 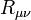 est le tenseur de Ricci.
est le tenseur de Ricci.
Diagonalisation de la métrique
Les conditions sur l'espace-temps décrites plus haut permettent de simplifier la métrique. Par exemple, la condition d'un espace-temps statique impose que si l'on applique la transformation de coordonnées
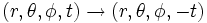 , les composantes gμ0 (où
, les composantes gμ0 (où  ) de la métrique changent de la manière suivante:
) de la métrique changent de la manière suivante: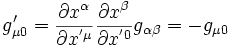 (
( )
)
Mais, on a imposé que gμ0' = gμ0. Ce qui implique que:
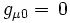 (
( )
)
De manière similaire, les transformations de coordonnées
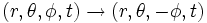 et
et 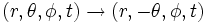 donnent respectivement:
donnent respectivement: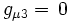 (
(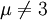 )
)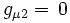 (
(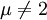 )
)
En combinant tous ces résultats, on obtient:
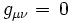 (
( )
)
En conséquence, la métrique a la forme suivante:
où les 4 composantes de la métrique (g11, g22,g33 et g00) sont indépendantes de la coordonnée de temps.
Simplification des composantes de la métrique
Sur chaque hypersurface où t, θ et φ sont constants (i.e. sur chaque ligne radiale), g11 ne doit dépendre que de r (par la condition de symétrie sphérique). Donc g11 est une fonction d'une seule variable:
Un argument similaire appliqué à g00 implique que:
Sur les hypersurfaces où t et r sont constants, on impose que la métrique est celle d'une 2-sphère:
En choisissant une de ces hypersurfaces (celle avec un rayon r0), les composantes de la métrique restreintes à cette surface (que l'on dénotera
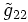 et
et 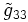 ) doivent être inchangées sous les opérations de rotation de θ et φ (de nouveau, par symétrie sphérique). Ainsi, comparant les formes de la métrique de cette hypersurface donne:
) doivent être inchangées sous les opérations de rotation de θ et φ (de nouveau, par symétrie sphérique). Ainsi, comparant les formes de la métrique de cette hypersurface donne:ce qui implique immédiatement:
 and
and 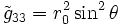
Comme cela est imposé pour chaque hypersurface (en d'autres termes pour une quelconque valeur de r), on a:
 and
and 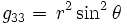
Ainsi, la métrique peut être écrite sous la forme:
où A et B sont des fonctions de r encore à déterminer. A et B doivent être non-nulles partout (ou alors la métrique serait singulière en ces points).
Équations de champs
Afin de déterminer les fonctions A et B, on utilise l'équation d'Einstein dans le vide mentionnée plus haut:
où Rμν = est le tenseur de Ricci. Parmi ces équations, seules 4 sont non-triviales, et après simplification, on obtient:
La quatrième équation étant simplement la deuxième multipliée par sin2θ. En soustrayant la première et la troisième, on obtient:
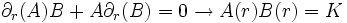
où K est une constante non-nulle. En remplaçant
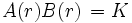 dans la deuxième équation, et en simplifiant, on a:
dans la deuxième équation, et en simplifiant, on a:
dont la solution générale est:
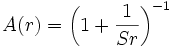
avec une constante réelle non-nulle S. En conséquence, la métrique pour une solution statique, symétriquement sphérique et dans le vide, s'écrit:
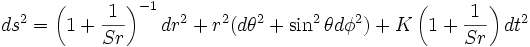
L'espace-temps représenté par cette métrique est asymptotiquement plat, ou, en d'autres termes lorsque
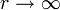 , la métrique s'approche de celle de Minkowski, et la variété de l'espace-temps ressemble à celle de l'espace de Minkowski.
, la métrique s'approche de celle de Minkowski, et la variété de l'espace-temps ressemble à celle de l'espace de Minkowski.Approximation du champ faible
Pour calculer les constantes K et S, on utilise l'«approximation du champ faible». En d'autres termes, on se place loin du centre, là où le champ de gravitation est faible. Dans ce cas, la composante g00 de la métrique peut être calculée:

où G est la constante gravitationnelle, m est la masse de l'objet central, et c est la vitesse de la lumière. Ainsi:
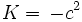 and
and 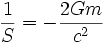
En conséquence,
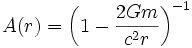 et
et 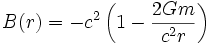
Dans ce cas, la métrique de Schwarzschild peut finalement s'écrire sous la forme suivante:
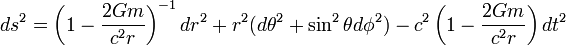 .
.Une singularité apparente est atteinte lorsque:
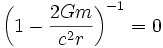 , ou, en d'autres termes, lorsque la coordonnée du rayon r vaut:
, ou, en d'autres termes, lorsque la coordonnée du rayon r vaut: .
.Ce rayon est appelé rayon de Schwarzschild. La singularité dans la métrique lorsqu'on atteint le rayon de Schwarzschild est dite apparente car il ne s'agit que d'un effet du système de coordonnées utilisées. Ici les coordonnées adoptées sont celles qui sont naturelles pour un observateur située très loin du corps céleste en question. Pour déterminer d'un point de vue physique et indépendant du système de coordonnées si on est en présence ou non d'une véritable singularité, c'est-à-dire pour laquelle les quantités physiques telles l'énergie, ou la pression, deviennent infinies, il est nécessaire de calculer la courbure de la métrique donnée par le tenseur de Riemann et de voir si ce dernier est singulier ou pas au niveau de l'horizon. La réponse est que la courbure n'est pas singulière lorsque l'horizon est atteint. De fait on peut trouver un jeu de coordonnées, plus adaptées pour un observateur comobile s'approchant du corps céleste, dans lequel la métrique est parfaitement régulière au niveau de l'horizon. Un observateur traversant l'horizon ne détecterait donc pas d'évènement particulier. Il s'agit des coordonnées de Kruskal qui sont discutées plus bas. Dans le cas idéalisé où le corps céleste est ponctuel au centre de la région interne à l'horizon, on peut montrer qu'il y existe une singularité, réelle cette fois-ci au sens où nous l'avons indiqué. En cet endroit un observateur détecterait nécessairement une divergence de toutes les quantités physiques observables.
L'horizon du trou noir de Schwarzschild
Au-delà de l'horizon: les coordonnées de Kruskal
La singularité
Lien externe
- (en) Schwarzschild Black Hole sur le site scienceworld.wolfram.com
- Portail de l’astronomie
- Portail de la physique
Catégorie : Trou noir - Un espace-temps avec symétrie sphérique, on dit aussi isotrope, est un espace-temps où toutes les composantes de la métrique sont inchangées lors d'une opération de rotation. Mathématiquement:
Wikimedia Foundation. 2010.